8 Вопрос Факторкольцо

[править]

Материал из Википедии — свободной энциклопедии

Факторкольцо́ — в абстрактной алгебре это кольцо классов вычетов некоторого кольца K по модулю его идеала J.

Обозначается K / J.

Классы вычетов по модулю идеала J определяются как смежные классы кольца K по аддитивной подгруппе J. Класс вычетов, содержащий элемент a обычно обозначается  . Два различных элемента кольца, принадлежащие одному классу вычетов, называются равными по модулю идеала.

Операции в факторкольце (сложение и умножение) определяются равенствами:

(a + J) + (b + J) = (a + b) + J

(a + J)(b + J) = ab + J

[Править]Связанные теоремы

• Теорема о гомоморфизме колец:

Если f — гомоморфизм кольца K на кольцо R, то ядро   является идеалом кольца K, причём кольцо R изоморфнофакторкольцу  .

Обратно: если J — идеал кольца K, то отображение  , определяемое условием  является гомоморфизмом кольца J на K / J с ядром J.

Теорема аналогична теореме о гомоморфизме групп.

• Факторкольцо   кольца   целых чисел по модулю главного идеала, порождённого простым числом p, является полем.

• Идеал J кольца K является простым (максимальным) в том и только в том случае, когда факторкольцо K / J является целостнымкольцом (полем).

9 Вопрос

В тетради

По́лем называется множество F с двумя бинарными операциями + (аддитивная операция, или сложение) и   (мультипликативная операция, или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей  , все ненулевые элементы которого обратимы.

Иными словами, множество F с двумя бинарными операциями + (сложение) и   (умножение) называется полем, если оно образуеткоммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойство дистрибутивности.

Связанные определения

• Характеристика поля — наименьшее положительное целое число n такое, что сумма n копий единицы равна нулю: 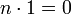     Если такого числа не существует, то характеристика равна 0 по определению.

• Подполем поля k называется подмножество, которое само является полем относительно операций сложения и умножения, заданных в k. (Подполем поля k называется поле относительно операций умножения и сложения, заданных в k, несущим множеством которого является подмножество несущего множества k)

• Расширение поля — поле, содержащее данное поле в качестве подполя.

• Поле Галуа — поле, состоящее из конечного числа элементов.

• Простое поле — поле, не содержащее собственных подполей.

[править]Свойства

• Характеристика поля всегда 0 или простое число.

  • Поле характеристики 0 содержит подполе, изоморфное полю рациональных чисел  .

  • Поле простой характеристики p содержит подполе, изоморфное полю вычетов   .

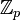• Количество элементов в конечном поле всегда равно pⁿ — степени простого числа.

  • При этом для любого числа вида pⁿ существует единственное (с точностью до изоморфизма) поле из pⁿ элементов, обычно обозначаемое  .

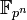• Любой ненулевой гомоморфизм полей является вложением.

• В поле нет делителей нуля.

[править]Примеры множеств, являющихся полями

•  — рациональные числа,

•  — вещественные числа,

•  — комплексные числа,

•  — поле вычетов по модулю p, где p — простое число.

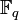•  — конечное поле из q = p^k элементов, где p — простое число, k — натуральное.

•  — поле рациональных функций вида f / g, где f и g — многочлены над некоторым полем   (при этом  , а f и g не имеют общих делителей, кроме констант).

• Числа вида 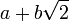 ,  , относительно обычных операций сложения и умножения.