1 Вопрос

Гру́ппа  — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам. Группы являются важными инструментами в изучении симметрии во всех её проявлениях. Примерами групп являются вещественные числа с операцией сложения,множество вращений плоскости вокруг начала координат и т. п. Ветвь математики, занимающаяся группами, называется теорией групп.

Определения

Непустое множество G с заданной на нём бинарной операцией   называется группой (G, * ), если выполнены следующие аксиомы:

1. ассоциативность:  ;

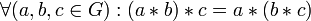2. наличие нейтрального элемента:  ;

3. наличие обратного элемента: 

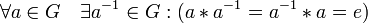
Связанные определения

Основная статья: Словарь терминов теории групп

• В общем случае от группы не требуется выполнения свойства коммутативности

  • Пары элементов 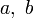 , для которых выполнено равенство a * b = b * a, называются перестановочными иликоммутирующими.

  • Множество элементов, перестановочных со всеми элементами группы, называется центром группы.

  • Группа, в которой любые два элемента коммутируют, называется коммутативной или абелевой.

• Подгруппа — подмножество H группы G, которое является группой относительно операции, определённой в G.

• Порядок группы (G, * ) — мощность G (то есть число её элементов).

  • Если множество G конечно, то группа называется конечной.

[Править]Примеры

• Целые числа с операцией сложения. 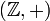  группа с нейтральным элементом 0. Она является абелевой.

• Положительные рациональные числа с операцией умножения. Произведение рациональных чисел — снова рациональное число, обратный элемент к рациональному числу представляется обратной дробью, имеется ассоциативность и единица.

• Свободная группа с двумя образующими (F₂) состоит из пустого слова, которое мы обозначаем ε (это единица нашей группы), и всех конечных слов из четырёх символов a,a ^{− 1},b и b ^{− 1} таких, что a не появляется рядом с a ^{− 1} и b не появляется рядом с b ^{− 1}. Операция умножения таких слов — это просто соединение (конкатенация) двух слов в одно с последующим сокращением парaa ^{− 1},a ^{− 1}a,bb ^{− 1} и b ^{− 1}b.

• Симметрическая группа. Множество всех биекций конечного множества в себя с операцией композиции является конечной группой, которая называется симметрической группой, или группой перестановок. Любая конечная группа является подгруппой некоторой симметрической группы (теорема Кэли).

• Циклические группы состоят из степеней 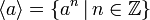  одного элемента a. Такие группы всегда коммутативны. Примеры таких групп — упомянутые уже целые числа по сложению и группа корней из единицы.

Простейшие свойства

• Обратный к данному элемент всегда определяется однозначно.

• (a⁻¹)⁻¹ = a, a^maⁿ = a^m+n, (a^m)ⁿ = a^mn.

• (ab)⁻¹ = b⁻¹a⁻¹.

• Верны законы сокращения:

,

.

• Обратный элемент к нейтральному есть сам нейтральный элемент.

• Группа содержит единственное решение x любого уравнения x · c = b или c · x = b; то есть в группе возможны однозначно определённые правое и левое «деление».

• Пересечение двух подгрупп группы G есть подгруппа группы G.

• Теорема Лагранжа: если G — группа конечного порядка g, то порядок g₁ любой её подгруппы G₁ является делителем порядка группы. Из этого следует, что и порядок любого элемента делит порядок группы.

• Для определения числа подгрупп в группе используются теорема Лагранжа и теоремы Силова.

Подгруппа ― подмножество H группы G, само являющееся группой относительно операции, определяющей G.

Подмножество H группы G является её подгруппой тогда и только тогда, когда:

1. содержит произведение любых двух элементов из H,

2. содержит вместе со всяким своим элементом h обратный к нему элемент h ^{− 1}.

В случае конечных и, вообще, периодических групп проверка условия 2 является излишней.

[править]Примеры

• Подмножество группы G, состоящее из одного элемента 1, будет, очевидно, подгруппой, и эта подгруппа называется единичной подгруппой группы G.

• Сама G также является своей подгруппой.

[править]Связанные определения

• Всякая подгруппа, отличная от всей группы, называется истинной подгруппой этой группы. Истинная подгруппа некоторой бесконечной группы может быть изоморфна самой группе.

• Сама группа G и единичная подгруппа называется несобственными подгруппами группы G, все остальные ― собственными.

• Пересечение всех подгрупп группы G, содержащих все элементы некоторого непустого множества M, называется подгруппой, порожденной множеством M, и обозначается < M > .

• Если M состоит из одного элемента a, то < a > называется циклической подгруппой элемента a.

  • Группа, совпадающая с одной из своих циклических подгрупп, называется циклической группой.

• Если группа G₁ изоморфна некоторой подгруппе H группы G, то говорят, что группа G₁ может быть вложена в группу G.

Свойства

• Теоретико-множественное пересечение любых двух (и любого множества) подгрупп группы G является подгруппой группы G.

• Теоретико-множественное объединение подгрупп, вообще говоря, не обязано являться подгруппой. Объединением подгрупп H иK называется подгруппа, порожденная объединением множеств  .

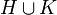• Гомоморфный образ подгрупп ― подгруппа.

• Если даны две группы и каждая из них изоморфна некоторой истинной подгруппе другой, то отсюда еще не следует изоморфизм самих этих групп.

Нейтральный элемент

Определение

Пусть   — множество M с определённой на нём бинарной операцией  . Элемент   называется нейтральным относительно  , если

Иногда различают нейтральный слева элемент  , для которого

и нейтральный справа элемент  , для которого

[править]Замечания

• В общем случае нейтральный слева и нейтральный справа элементы могут не совпадать или же не существовать.

• В приведённой выше мультипликативной нотации нейтральный элемент принято называть «единичным элементом» или просто «единицей». Если для обозначения операции используется аддитивная нотация + , то нейтральный элемент называют «нулём» (не путать с числами 1 и 0, соответственно).

[править]Примеры

Множество	Бинарная операция	Нейтральный элемент
Вещественные числа	+ (сложение)	число 0
Вещественные числа		число 1
Вещественные числа	ab (возведение в степень)	число 1 (нейтральный справа)
Матрицы размера	+ (матричное сложение)	нулевая матрица
Матрицы размера	(матричное произведение)	единичная матрица
Функции вида	(композиция функций)	тождественное отображение
Функции вида	* (свёртка)	δ (дельта-функция)
Символьные строки	конкатенация	пустая строка
Расширенная числовая прямая	(минимум) или inf  (инфимум)
Расширенная числовая прямая	(максимум) или sup  (супремум)
Подмножества множества M	(пересечение множеств)	M
Множества	(объединение множеств)	(пустое множество)
Булева логика	(логическое и)	(истина)
Булева логика	(логическое или)	(ложь)

Определения

• Пусть   — множество M с определённой на нём бинарной операцией  . Пусть 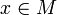  — произвольный элемент множества M. Если справедливо равенство 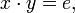     где 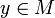 , а   - нейтральный элемент относительно операции  , то y называется обра́тным спра́ва к x.

• Аналогичным образом, если выполнено 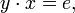     то y называется обра́тным сле́ва к x.

• Элемент  , являющийся обратным к x и справа, и слева, то есть такой, что 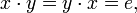     называется просто обратным к x и обозначается x ^{− 1}.

• Элемент, для которого существует обратный элемент, называется обратимым.

[править]Замечания

• Приведённое выше определение дано в мультипликативной нотации. Если используется аддитивная нотация (M, + ), то обратный элемент называется противополо́жным и обозначается − x.

• Вообще говоря, один и тот же элемент   может иметь несколько обратных слева элементов и несколько обратных справа элементов, и последние не обязаны пересекаться.

[править]Свойства

• Пусть операция   ассоциативна. Тогда если для элемента   определены обратный слева и обратный справа элементы, то они равны и единственны.

[править]Примеры

Множество	Бинарная операция	Обратный элемент
Вещественные числа	+ (сложение)	− x (противоположное число)
Вещественные числа не равные нулю	(умножение)	1 / x (обратное число)
Функции вида	(композиция функций)	f − 1 (обратная функция)