2 Вопрос

Порядок элемента g группы G — минимальное натуральное число m такое, что g^m = e. В случае, если такого m не существует, считается, что g имеет бесконечный порядок.

Циклическая группа

В теории групп группа называется циклической, если она может быть порождена одним элементом a, то есть все её элементы являются степенями a (или, если использовать аддитивную терминологию, представимы в виде na, где n — целое число). Математическое обозначение: .

Несмотря на своё название, группа не обязательно должна буквально представлять собой «цикл». Может случиться так, что все степени gⁿ будут различными. Порождённая таким образом группа называется бесконечной циклической группой и изоморфна группе целых чисел по сложению ( ).

Свойства

Все циклические группы абелевы.
Каждая конечная циклическая группа изоморфна группе — со сложением по модулю n (её также обозначают ), а каждая бесконечная — изоморфна , группе целых чисел по сложению.
- В частности, для каждого натурального числа n существует единственная (с точностью до изоморфизма) циклическая группапорядка n.
Каждая подгруппа циклической группы циклична.
У циклической группы порядка n существует ровно φ(n) порождающих элементов, где φ — функция Эйлера
Если p — простое число, то любая группа порядка p циклическая и единственна с точностью до изоморфизма (это следует изтеоремы Лагранжа).
Прямое произведение двух циклических групп порядков n и m циклично тогда и только тогда, когда n и m взаимно просты.
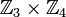- Например, изоморфна , но не изоморфна .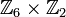
Основная теорема о конечнопорождённых абелевых группах утверждает, что любая конечнопорождённая абелева группаединственным образом разлагается в прямое произведение примарных циклических групп. Примарной группой может быть циклическая группа 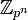, где p — простое число, или .
Мультипликативная группа любого конечного поля является циклической (она порождается элементом поля наибольшего порядка).
Кольцо эндоморфизмов группы изоморфно кольцу . При этом изоморфизме числу r соответствует эндоморфизм , который сопоставляет элементу сумму r его экземпляров. Такое отображение будет биекцией, если и только если r взаимно просто с n, так что группа автоморфизмов изоморфна .

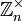[править]Примеры

Группа корней из единицы степени n по умножению.
Группа Галуа любого конечного расширения конечного поля конечна и циклична; обратно, если дано конечное поле F и конечная циклическая группа G, существует конечное расширение F группой Галуа которого будет G.

[править]Доказательства

Утверждение. Каждая подгруппа циклической группы циклична.

Доказательство. Пусть G — циклическая группа и H — подгруппа группы G. Если группа G тривиальна (состоит из одного элемента), то H = G и H циклична. Если H — тривиальная подгруппа (состоит из единичного элемента или совпадает со всей группой G), то H циклична. Далее в ходе доказательства будем считать, что G и H не являются тривиальными.