19. Теорема Гаусса в дифференциальной форме. Плотность тока смещения.

С помощью интегральной теоремы Гаусса нельзя определить, как связан исток линий в данной точке поля с плотностью свободных зарядов в той же точке поля. Поэтому переходят к записи теоремы Гаусса в дифференциальной форме:

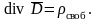(15.16)

Исток линий в данной точке поля определяется величиной плотности свободных зарядов в этой точке (рис. 15.4).

Если среда однородна и изотропна, т.е. _a = const, то можно записать:

(15.17)

или:

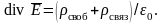(15.18)

Рис. 15.4. К пояснению истока линий вектора

Истоком вектора в отличие от истока вектора являются не только свободные, но и связанные заряды.

С другой стороны известно, что

С учетом этого

Или

(15.19)

Уравнение (15.19) называется уравнением Пуассона. Частный вид уравнения Пуассона при _св = 0, называется уравнением Лапласа

.

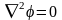Эти два уравнения являются основными уравнениями электростатики. Уравнение Пуассона выражает связь между частными производными второго порядка от  в любой точке поля и плотностью свободных зарядов в этой точке поля.

Решение уравнения Пуассона в общем виде можно найти следующим образом. Положим, что в объеме V есть объемные , поверхностные  и линейные  заряды. Эти заряды представим в виде совокупности точечных зарядов: dV, ds и dl, где dV – элемент объема, ds – элемент заряженной поверхности, dl – элемент длинны заряженной оси. Составляющая потенциала d в некоторой точке пространства, удаленной от dV на расстояние r, в соответствии с формулой (15.15) равна

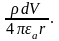
Аналогично можно определить составляющие потенциала от поверхностного и линейного зарядов

и .

Полное значение  определяется как сумма (интеграл) составляющих потенциала от всех зарядов поля:

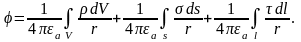(15.20)

В формуле (15.20) ,  и  есть функции радиуса r, которые практически определить очень трудно. Предполагается, что потенциал на бесконечности равен нулю и заряды, создающие поля распределены в ограниченной области (иначе интеграл может оказаться расходящимся).

. Вектор плотности тока смещения в диэлектрике

(14.32)

наблюдается в диэлектрике только в переменном во времени поле. Может происходить выделение теплоты, но не по закону Джоуля-Ленца. На поверхности проводника .

21.Частными видами электромагнитного поля являются:

1. Электростатическое поле, которое создается неподвижными заряженными телами и проявляется в виде механической силы, действующей на неподвижный электрический заряд. Это поле потенциально, т.е. rot = 0.

2. Электрическое поле постоянного тока (стационарное электрическое поле) образуется внутри и вне проводников при прохождении по ним постоянного тока. При этом внутри однородного проводника отсутствует объемная плотность заряда, т.е. div   = 0. Поле является потенциальным и для него справедливо уравнение Лапласа ² = 0.

3. Магнитное поле постоянного потока проявляется в силовом воздействии на движущиеся в нем заряженные тела и на неподвижные контуры с постоянным током. Поле имеет вихревой характер ( ).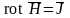

Электрическое поле постоянного тока и магнитное поле постоянного потока могут рассматриваться независимо друг от друга.