16. Способы согласования линии без потерь с нагрузкой

Если линия нагружена на активное сопротивление , то последовательно с нагрузкой включают отрезок линии длиной в четверть волны (рис. 13.16).

Для согласования необходимо, чтобы .

Для линии без потерь согласно (11.44) входное сопротивление

Рис. 13.16. Согласование линии с помощью четвертьволнового трансформатора

В данном случае

Так как tg /4 = , то .

Следовательно, для согласования линии с нагрузкой требуется подобрать такую линию (длиной четверть волны), у которой волновое сопротивление будет

(13.54)

Так как такая линия преобразует (трансформирует) сопротивление нагрузки, то ее называют четвертьволновым трансформатором.

Если нагрузка представляет собой активно-реактивное сопротивление, то для согласования применяют параллельное соединение четвертьволнового трансформатора и шлейфа (рис. 13.17).

Путем подбора волнового сопротивления четвертьволнового трансформатора добиваются согласования активной проводимости цепи трансформатор-нагрузка, а затем с помощью шлейфа компенсируют реактивную составляющую проводимости ветви с трансформатором

Z_H = R_H + j X_H;

;

;

;

;

;

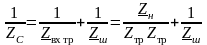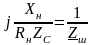. (13.55)

В зависимости от характера нагрузки применяют шлейф, работающий в режиме короткого замыкания (X_H > 0) или холостого хода (X_H < 0).

Аналогично можно показать, что для согласования шлейф можно включить последовательно с нагрузкой и четвертьволновым трансформатором (рис. 13.18).

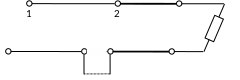
Рис. 13.18. Согласование линии с помощью четвертьволнового трансформатора и последовательного шлейфа

Сопротивление шлейфа находится из соотношения

. (13.56)

17 . Основные операторы и векторные операции

Электромагнитное поле – это вид материи, определяемый во всех точках двумя векторными величинами, которые характеризуют две его стороны, называемые электрическим полем и магнитным полем, и оказывающий силовое воздействие на заряженные частицы, зависящее от их скорости и заряда.

Основным математическим аппаратом при расчете электромагнитного поля является векторный анализ, включающий в себя понятия: скаляр, вектор и тензор. В общем случае скаляры и векторы являются функциями координат точки и времени. При анализе электромагнитного поля применяют линейный, поверхностный и объемный интегралы, а также дифференциальные операторы.

Оператор – это символ, характеризующий действие над вектором или скаляром, расположенным после символа.

Дифференциальные операторы позволяют сократить запись различных операций над скалярными и векторными величинами.

18.Формы записи уравнений Максвелла (+20)

Уравнения Максвелла являются фундаментальными уравнениями электромагнитного поля. Эти уравнения могут быть записаны в интегральной, дифференциальной или комплексной форме. Интегральная форма записи уравнений устанавливает связь между величинами в разных точках поля или на разных отрезках, поверхностях. Дифференциальная форма описывает соотношение между величинами вблизи одной и той же точки поля в определенный момент времени. Эту форму записи применяют при исследовании полей, изменяющихся от точки к точке. Гармонически изменяющиеся электромагнитные поля (когда проекции вектора на координатные оси являются гармоническими функциями времени) удобно характеризовать уравнениями Максвелла в комплексной форме.

Переход от интегральной формы записи уравнений к дифференциальной осуществляется с помощью теорем Остроградского-Гаусса и Стокса (14.20) и (14.21).

Система уравнений электромагнитного поля включает в себя четыре основных уравнения Максвелла и уравнения связи между векторами поля и параметрами , характеризующими свойства среды.

1. Закон полного тока – первое уравнение Максвелла

. (14.37)

Ток смещения , также как и ток проводимости , создает магнитное поле. Изменяющееся во времени электрическое поле создает магнитное поле. Направление вектора напряженности магнитного поля связано с направлением полного тока и определяется правилом правоходового винта.

2. Закон электромагнитной индукции – второе уравнение Максвелла

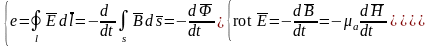(14.38)

Изменение магнитной индукции во времени создает электрическое поле, направление которого связано с направлением и определяется правилом левоходового винта.

3. Принцип непрерывности магнитных силовых линий

. (14.39)

Магнитный поток через замкнутую поверхность равен нулю. Магнитные силовые линии всегда замкнуты и не имеют ни истоков, ни стоков.

4. Обобщенная теорема Гаусса

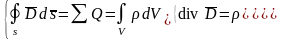(14.40)

Поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме свободных зарядов, находящихся внутри замкнутой поверхности.

5. Уравнения связи между векторами и , и , 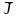и в материальной среде

. (14.41)