1 Комплексные числа. Алгебраические операции над комплексными числами

1.1 Определение комплексного числа. Формы записи комплексных чисел

Определение. Комплексным числом называется пара действительных чисел , записанных в определенном порядке: . Одним из его обозначений служит запись вида

, (1)

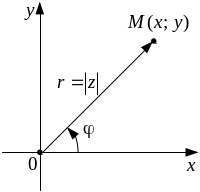
Рисунок 1

называемая алгебраической формой записи комплексного числа . B записи (1) называется действительной, - мнимой частями комплексного числа (употребляется также обозначения , ); называется "мнимой единицей".

Для геометрического изображения комплексного числа вводят на плоскости прямоугольную декартову систему координат ; ось называется действительной осью, – мнимой, плоскость – комплексной плоскостью . Комплексному числу можно поставить в соответствие точку плоскости , либо вектор – и точка и вектор служат геометрическим изображением комплексного числа , (см. рисунок 1). Модуль вектора называется модулем комплексного числа ; он определяется по формуле

. (2)

Угол между действительной осью и вектором называется аргументом комплексного числа : . Значение , заключенное в промежутке , называется главным значением аргумента и обозначается: .

(3)

Следовательно,

. ( )

Главное значение аргумента комплексного числа можно определить по формуле:

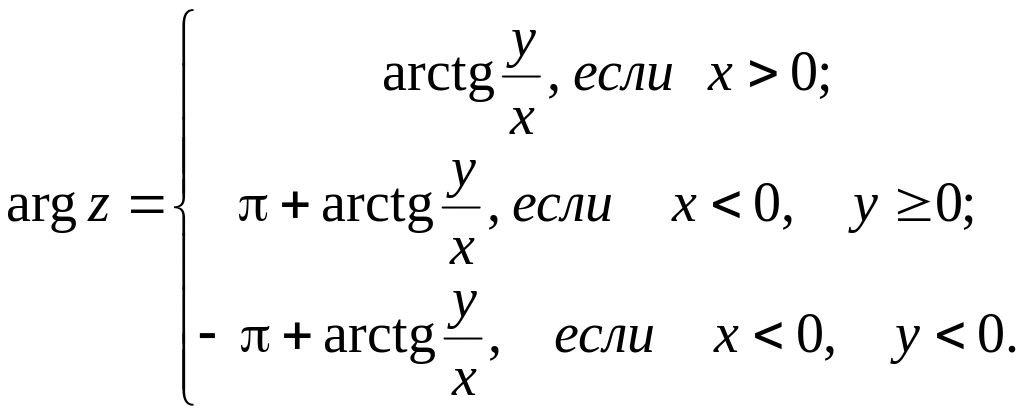(4)

Определение. Запись вида

(5)

называется – тригонометрической формой записи комплексного числа .

Замечание. Комплексное число записывается также в показательной форме

. ( )

Для сравнения комплексных чисел и вводится лишь операция равенства: комплексные числа и равны если равны соответственно их действительные и мнимые части: , . Равенство чисел, записанных в тригонометрической форме, формулируется следующим образом: , если модули их равны: , а аргументы связаны соотношением

(6)

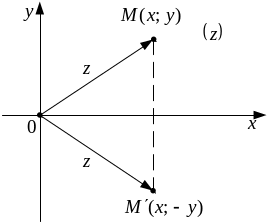
Рисунок 2

(следует обратить внимание на то, что здесь сравниваются не элементы множества, а сами бесконечные множества).

Определение. Два комплексных числа и называются комплексно-сопряженными числами. Для этого употребляют обозначение и (см. рисунок 2).

1.2 Действия над комплексными числами

Действия сложения и вычитания над комплексными числами определяются геометрически, т.е. как соответствующие действия над векторами (см. рисунок 3) и, следовательно, выполняются по формулам:

, (7)

(8)

– чтобы, например, сложить два комплексных числа, нужно сложить отдельно действительные и мнимые части. Получившиеся суммы будут соответственно действительной и мнимой частями суммы чисел.

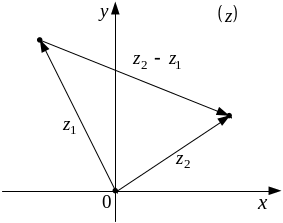
Рисунок 3

Из формул (7) и (8) находим

(9)

Под произведением комплексных чисел и (обозначается ) понимается комплексное число , равное

. (10)

Деление комплексных чисел и определяется через действие умножения и может быть проведено по формуле

. (11)

Так как по формуле (10) , то деление удобно выполнять по следующей формуле:

( )

Введенные таким образом операции сложения и умножения комплексных чисел подчиняются известным пяти законам арифметики:

1) – коммунитативность сложения;

2) – ассоциативность сложения;

3) – коммунитативность умножения;

4) – ассоциативность умножения;

5) – дистрибутивность умножения относительно сложения.

Формула (10) "раскрывает смысл" "мнимой единицы" . Таким образом, умножение комплексных чисел производится по обычным правилам алгебры с заменой на .

Приведем решение "типовых примеров" на введенные выше понятия.

Пример 1. Показать, что .

По определению суммы и ее свойств имеем:

Пример 2. Найти действительные решения уравнения .

Запишем левую часть уравнения в алгебраической форме: . По определению равенства комплексных чисел получим систему уравнений , , решением которой является пара чисел , .

Пример 3. Решить систему уравнений:

Так как , то система имеет единственное решение, которое можно найти по формулам Крамера. Имеем

и, следовательно,

Пример 4. Для числа :

а) построить геометрическое изображение;

б) найти модуль и главное значение аргумента;

в) записать число в тригонометрической форме;

г) записать число в показательной форме.

Число представлено, очевидно, в алгебраической форме (не имеет вида (5)):

Рисунок 4

На рисунке 4 число представлено геометрически. Найдем модуль комплексного числа . По формуле (2) имеем

Так как точка расположена в третьем квадранте , главное значение аргумента числа следует вычислить по третьей строчке формулы (4):

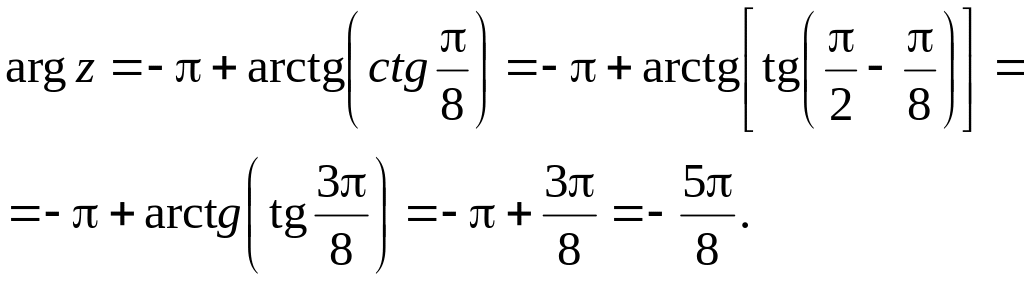
Таким образом, . Запишем в тригонометрической форме: и показательной форме: .