4.2 Теорема Коши. Интегральные формулы Коши
Теорема
Коши. Если
функция
аналитична
в односвязной области, ограниченной
контуром
,
и
– замкнутый контур в
,
то
. (53')
Если,
помимо того, функция
непрерывна в замкнутой области
,
то
(53)
– теорема Коши для односвязной области.
Если
функция
аналитична в многосвязной области
,
ограниченной
внешним контуром
и внутренними контурами
и непрерывна
в замкнутой области
,
то (контур
обходится
в положительном направлении)
(54)
– теорема Коши для многосвязной области. Дадим другую формулировку этой теоремы:
(55)
– интеграл по внешнему контуру равен сумме интегралов по внутренним контурам (все контуры проходятся в одном и том же направлении).
Если
аналитична
в области
,
и
– контур, охватывающий точку
,
то справедлива интегральная
формула Коши
. (56)
При этом функция имеет всюду в производные любого порядка, для которых справедлива формула
. (57)
Пример
1. Вычислить
.
Внутри
окружности
знаменатель дроби обращается в нуль в
точке
.
Для удобства применения формулы (56)
перепишем интеграл в виде
.
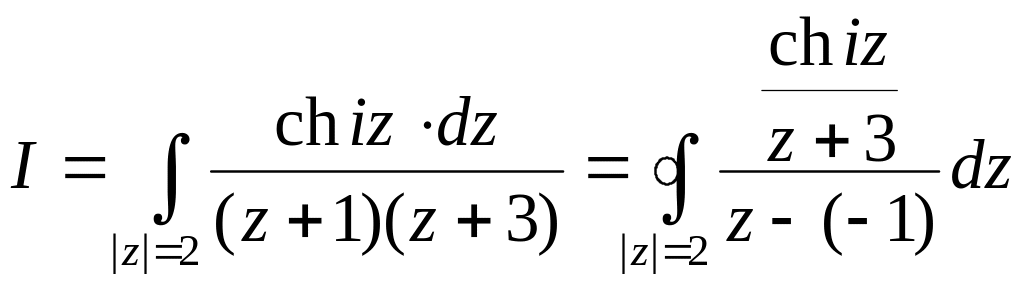Здесь
и
аналитична в круге
.
Тогда
.
Пример
2. Вычислить
:
по а) контуру
;
б)
.
а)
в круге
функция
аналитична; следовательно, по формуле
(53)
;
б)
так как внутри контура интегрирования
знаменатель подынтегральной функции
обращается в нуль в точках
и
,
то для того, чтобы стало возможным
применить формулы (56) и (57), рассмотрим
многосвязную область
(рисунок 15), ограниченную окружностью
и внутренними контурами
и
.
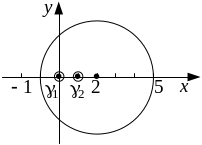
Рисунок 15
Тогда
в области
функция
является аналитической, и по теореме
(55) можно записать:
.
Для вычисления интегралов справа
применим формулы (56)
и (57):
;
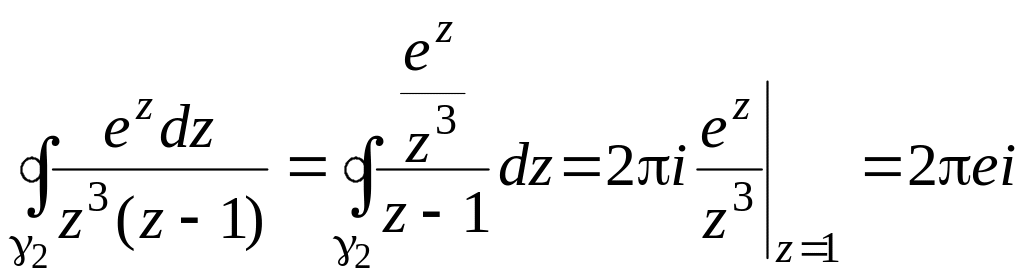и,
таким образом,
.
4.3 Задачи для самостоятельного решения
Вычислить интегралы по заданным контурам:
1.
.
2.
.
3.
.
4.
.
5.
отрезок
от точки
до точки
.
6.
.
7.
.
8.
.
9.
.
Применяя теоремы и интегральные формулы Коши, вычислить интегралы:
10.
.
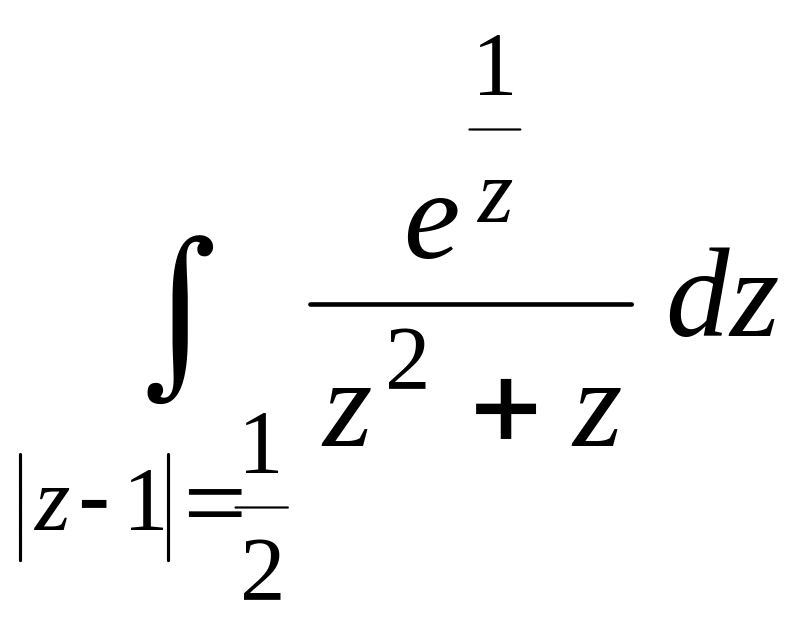11.
.
12.
.
13.
.
14.
.
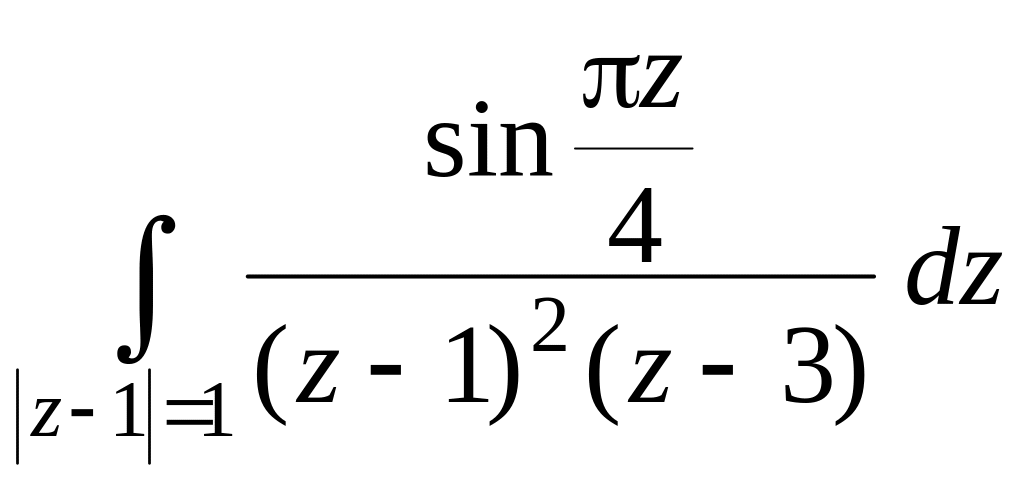15.
.
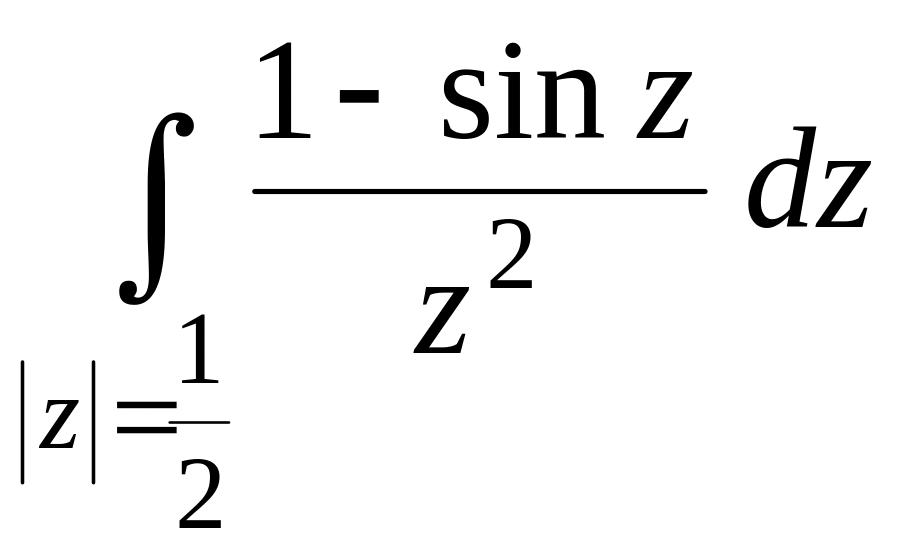