Генерация псевдослучайных чисел
Наиболее часто применимым на практике методом получения СВ являются генерация одной или нескольких СВ, равномерно распределенных на интервале [0,1] (базовая СВ или БСВ), и последующее преобразование БСВ в новую СВ, распределенную по нужному закону.
Из
всех методов получения СВ предпочтение
отдается применению рекурсивных формул,
по которым на основании
-й
СВ вычисляется (
+1)-я
СВ. Наилучшим образом требованиям СВ
удовлетворяет конгруэнтный метод:
= (
+
)
,
=0,1,2,…,
=
/
,
где , , - константы; - ненормализованная СВ; - нормализованная СВ в интервале [0,1]; ( + ) означает, что
=
(
+
)
-
{
},
где
{} - целая часть;
=
- корень. Числа
являются не точно случайными
(псевдослучайными) и могут повторяться
(имеют период числового ряда). Для данных
конгруэнтных генераторов полный период
(
-
разрядность ЭВМ) соответствует
=
,
- простое к
число (наибольший общий делитель равен
1),
=1+4
, где
- целое число.
Для параллельных случайных потоков можно использовать один и тот же генератор с разными .
Фундаментальным
методом получения СВ с заданным законом
распределения
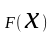является метод обратной функции:
=
,
где
-
БСВ,
-
функция от
,
вычисляемая из уравнения
= .
Пример:
.
Генерируем число r
и приравниваем его к
.
После логарифмирования равенства r=
находим
=
=-
ln
r.
Если функцию найти не удается, используют процедуры (программы) случайной выборки.
Основные понятия математической статистики
Сбор данных. Источники данных до моделирования: документация, анкетирование, эксперимент. Во время имитационного прогона сбор данных ведется автоматически.
Описание статистических данных. Имеет целью их формализацию для выявления наиболее важных свойств.
преобразования данных к удобному
формальному виду является группировка
п
Кл2
о классам Кл (интервалам И), отображающая
количество (частоту) попадания данных
Кл1
Кл3
в каждый класс (число классов
).
Результаты
либо помещают в таблицу, либо отображают
И
графически, например, в виде гистограмм (рис.8.8).
Рис.8.8
Рекомендации: а) И=const; б) классы не должныперекрываться; в) 5 20.
Оценка параметров. Полученные в том или ином виде ограниченные данные обычно рассматривают как выборки для оценки параметров всей их генеральной совокупности (табл.8.1).
Оценка чувствительности. Для оценки чувствительности к параметру вначале задают его относительное среднее изменение:
=
.
Затем
проводят два прогона для
=
и
=
и средних фиксированных значений
остальных параметров. Определяют отклики
модели
=
(
),
=
(
)
и относительное приращение наблюдаемой
переменной
Таблица 8.1. Оценка параметров
Статистика |
Формула |
|
Точечные оценки |
Интервальные оценки |
|
Выборочное среднее |
=
|
=
|
Дисперсия выборки |
|
=
|
,
-
интервал СВ;
:
(0)
=
;
(
)
=
+
;
…
=
-
.
Аналогично
формируются другие пары (
,
)
с разными приращениями для исследования
функции
=
(
).
Подбор распределения. Удачный выбор распределения полученных данных дает эффективный аппарат для обработки данных по всем интересующим критериям. Подбору способствуют детальное знакомство с видами распределений и практика. Для подбора закона распределения необходимо использовать готовые программные средства либо эвристический способ с оценкой выбора на основе статистического вывода.
Статистический вывод. Поскольку имитационная модель содержит вероятностные элементы, результаты имитации являются наблюдениями случайных величин. Их обработку необходимо делать на основе доверительных интервалов или проверкой гипотез.
Доверительные интервалы. Мерой точности оценки данных является доверительный интервал (ДИ). Он характеризует величину наибольшего отклонения оцениваемого параметра от истинного значения. Поскольку отклонение имеет два знака, то доверительный интервал есть удвоенный модуль максимально допустимого отклонения. Необходимо учесть, что любые события имеют вероятность появления. Вероятность попадания оцениваемого параметра в доверительный интервал называют доверительной вероятностью. Так, на основе статистики Стьюдента можно утверждать, что с вероятностью 1- (доверительная вероятность) МО попадает в доверительный интервал:
.
Проверка гипотез. Процедура проверки гипотез требует определения нулевой гипотезы (H0) и альтернативной (H1). Проверка ведется по выбранным критериям.
-критерий
служит для контроля средних значений.
Гипотеза H0:
=
.
Альтернативная гипотеза H1:
.
Тест-проверка:
=
.
Если
,
то гипотезу H0
отвергают.
-критерий (критерий согласия Пирсона) используют при наличии гистограмм:
=
-
,
где
- число интервалов (классов),
- теоретическая вероятность попадания
в
-й
интервал (по предполагаемому закону
распределения),
- практическое число попаданий в
-й
интервал. Из таблицы
-распределения
находят верхний порог значимости
(квантиль)
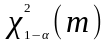(где
)
для выбранного
.
Значение
сравнивают с
:
1) приемлемо, если
(гипотеза H0);
2) не приемлемо, если
(гипотеза H1).
Планирование имитационных экспериментов. Имитационный прогон - это эксперимент, в котором осуществляются исследование и оценка функционирования системы при заданном наборе условий. В терминах теории планирования эксперимента условия называются факторами, а некоторое конкретное значение фактора - уровнем.
К задачам планирования относятся задание начальных условий, процедура выборок, определение продолжительности и числа прогонов, определение пространства выводов о реальной системе, выбор средств имитационного моделирования, объем и вид документации о результатах моделирования.
Задание начальных условий. Предлагаются три правила. 1. Запустить модель с состояния "пуст и свободен". Достоинство - простота. Недостаток - неопределенность начального состояния. 2. Запустить модель с модальных (с максимальной вероятностью) значений. Достоинство - начало соответствует наиболее вероятному состоянию системы. Недостаток - трудность определения модальных значений априори. 3. Запустить модель со средних значений. Достоинство - относительная простота определения средних значений. Недостаток - мала вероятность их.
Процедура выборок. Выборки могут осуществляться через заданный интервал имитационного времени или при наступлении определенных событий. Важное значение имеет момент начала сбора статистических данных, так как начальные условия могут исказить результат имитации. Поэтому целесообразно за счет уменьшения количества собранной информации отсечь начальный участок прогона.
Продолжительность и число прогонов. Пространство выводов. Однофакторный дисперсионный анализ. Корреляционный и регрессивный анализы. Обобщенные оценки.
Продолжительность и число прогонов. Использование нескольких продолжительных прогонов предпочтительней множества коротких. Продолжительность прогона можно контролировать по оценке исследуемого параметра: имитация прекращается, когда оценка дисперсии среднего выборочного становится меньше заданной величины.
Число независимых повторных прогонов для достижения заданного доверительного интервала 1- равно
=
(
)2,
где
=
- среднеквадратичное отклонение
переменной
;
- половина доверительного интервала
(точность оценки). Поскольку сами
параметры
,
основаны на статистике, сначала делают
любые
прогонов, находят
(по разбросу выборок
),
(по таблице
-распределения
Стьюдента для заданной доверительной
вероятности и
=
-1),
а затем уточняют
по
и
.
Итерационные уточнения можно делать
неоднократно.
Определение пространства выводов. Пространство выводов касается диапазона изменения входных данных, чувствительности к уровням факторов, класса объектов, исследование которых можно проводить с данной имитационной моделью.
Однофакторный дисперсионный анализ. Суть однофакторного дисперсионного анализа сводится к определению влияния на результат моделирования одного выбранного фактора. Для доказательства независимости какого-либо параметра от выбранного фактора достаточно проверить гипотезу о равенстве средних значений выборок при различных значениях исследуемого фактора.
Корреляционный анализ. Позволяет делать статистические выводы о степени зависимости между переменными. Величина линейной зависимости между двумя переменными измеряется посредством коэффициента корреляции без учета влияния других переменных.
Регрессионный анализ. На основе уравнений регрессии уточняет форму зависимости между переменными. Так, например, простая линейная регрессия для переменных , имеет вид:
=
+
+
,
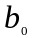где
=0,
1,…,
;
- коэффициент регрессии;
- случайные ошибки испытаний, которые
при модельной оценке
для заданного
полагают равными нулю (
не известны при имитации). Цель
регрессионного анализа - найти наилучшие
в статистическом смысле оценки параметров
,
.
Для этого при выбранных начальных
параметрах
,
находят отклонение
между предполагаемым (по уравнению)
и его экспериментальным
значениями. Далее строят график
зависимости
=
(
).
По виду графика делают заключение о
степени адекватности модели и о
направлении изменения исходных значений
,
.
Обобщенные оценки. Информационные системы, как правило, относятся к системам массового обслуживания. Анализ таких систем ведут на основе общих средних значений параметров. Рассмотрим примеры обобщенных оценок.
Простейшими системами являются системы с одним прибором, обрабатывающим поступающие запросы. Для них наибольший интерес представляет усредненное время ожидания и обслуживания при различных коэффициентах использования оборудования
=
.
Учитывая случайный характер поступления заявок, более точно коэффициент использования рассчитывают как
=
,
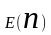
где
- среднее число поступивших запросов в
единицу времени,
-
среднее время обслуживания одной заявки.
Тогда среднее время пребывания одной
заявки в системе
=
+
,
где
-
среднеквадратичное отклонение времени
обслуживания или его оценка по некоторому
объему выборок.
Среднее время нахождения в очереди одной заявки есть
=
.
Среднее число заявок в очереди
=
+
.
Среднее число заявок, ожидающих обслуживание,
=
.
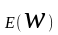Если
в многоприборной последовательной
системе одинаково загружены все
приборов (к этому необходимо стремиться),
то для каждого прибора
= / ,
где , - параметры всей системы. В системах со многими направлениями, параллельными процессами и переключаемой структурой обобщенная оценка параметров усложняется.
Системы имитации GPSS и СЛАМ II. Общая характеристика пакета MATLAB. Подсистемы Simulink.
GPSS
Система GPSS предназначена для моделирования дискретных объектов процессно-ориентированным способом на языке GPSS. Модель представляет собой сеть, составленную из блоков, выполняющих определенные функции. Сеть дополняется программной частью. Таймер GPSS регистрирует только целочисленные значения времени.
Пример. Интервалы прихода заявок на пункт приема распределены равномерно в диапазоне 186 единиц времени. Время обработки заявки распределено также равномерно в диапазоне 164 единицы. Заявки приходят, обрабатываются и пересылаются на выполнение. Необходимо собрать статистические данные об очереди заявок за 8 часов. Сетевая модель имеет вид рис.9.1.
GENERATE
480
GENERATE
18.6
1-й
сегмент
2-й
сегмент
JOEQ
TERMI-NATE
QUEUE
1
JOE
SEIZE
TERMI-NATE
JOEQ
DEPART
ADVANCE
16.4
RELEASE
JOE
Рис.9.1
Здесь для первого сегмента:
GENERATE - операция генерации транзактов с интервалом 186;
QUEUE - "встать в очередь" JOEQ;
SEIZE - "занять свободный прибор (обработки)" JOE;
DEPART - "покинуть очередь" JOEQ;
ADVANCE - "задержать" на 164;
RELEASE - "освободить прибор" JOE;
TERMINATE - "завершить" (покинуть).
2-й сегмент моделирует окончание имитации. При выходе из TERMINATE счетчик завершений уменьшает показания на 1.