
Глава 6 Поверхности второго порядка
Если в пространстве
![]() ввести прямоугольную систему координат
ввести прямоугольную систему координат
![]() то каждая поверхность определяется
некоторым уравнением
то каждая поверхность определяется
некоторым уравнением
![]() ,
,
![]() - координаты любой точки поверхности.
Если
- координаты любой точки поверхности.
Если
![]() - многочлен не выше второй степени
относительно совокупности переменных
- многочлен не выше второй степени
относительно совокупности переменных
![]() ,
то уравнение
называется уравнением второго порядка,
а поверхность, изображаемая этим
уравнением называется поверхностью
второго порядка.
,
то уравнение
называется уравнением второго порядка,
а поверхность, изображаемая этим
уравнением называется поверхностью
второго порядка.
Если поверхность имеет специфическое расположение относительно системы координат (например, симметрична относительно некоторых координатных плоскостей, или имеет вершину в начале координат), то ее уравнение имеет достаточно простой вид, который называется каноническим.
§1 Канонический вид уравнений поверхностей второго порядка. Геометрическое изображение
Сферой называют
множество точек пространства
![]() ,
которые равноудалены от точки, называемой
центром сферы на расстояние, называемое
радиусом сферы.
,
которые равноудалены от точки, называемой
центром сферы на расстояние, называемое
радиусом сферы.
Сфера радиуса
![]() с центром в начале координат (рисунок
96)
с центром в начале координат (рисунок
96)
![]() (60)
(60)
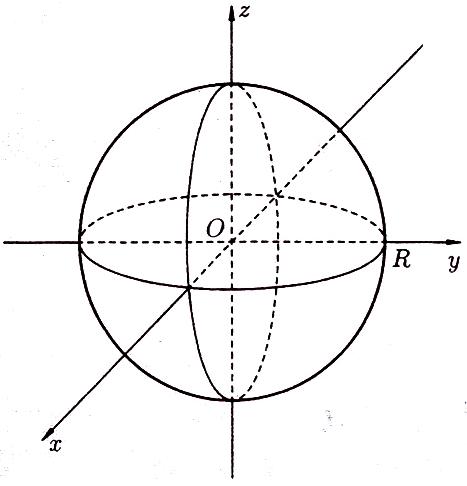
Рисунок 96
Уравнение
![]() (61)
(61)
изображает сферу
радиуса
с центром в точке
![]() .
.
Эллипсоид с
полуосями
![]() и центром в начале координат (рисунок
97)
и центром в начале координат (рисунок
97)
![]() (62)
(62)
При
![]() эллипсоид превращается в сферу радиуса
.
эллипсоид превращается в сферу радиуса
.
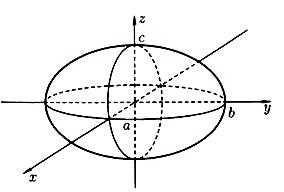
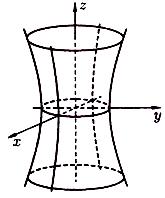
Рисунок 97 Рисунок 98
Однополостный
гиперболоид с полуосями
и осью
![]() (рисунок 98)
(рисунок 98)
![]() (63)
(63)
Сечения гиперболоида
горизонтальными плоскостями
![]() являются эллипсами:
являются эллипсами:
![]() .
.
Сечения гиперболоида
вертикальными плоскостями
![]() или
или
![]() являются гиперболами:
являются гиперболами:
![]() или
или ![]() .
.
Двуполостный гиперболоид с полуосями и осью (рисунок 99)
![]() (64)
(64)
Сечения гиперболоида
горизонтальными плоскостями
,
![]() являются эллипсами:
являются эллипсами:
![]() .
.
Сечения гиперболоида
вертикальными плоскостями
или
являются гиперболами:
![]() или
или ![]() .
.
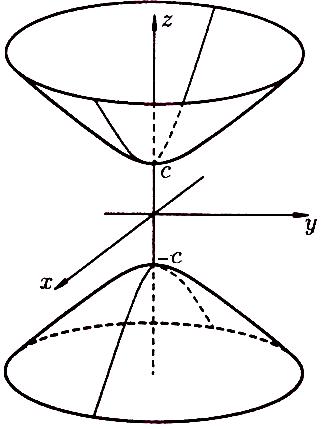
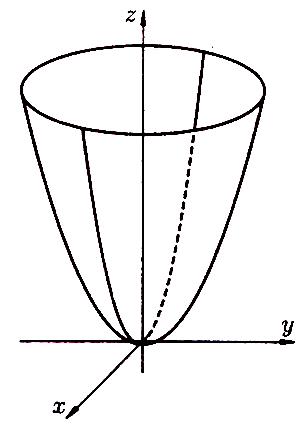
Рисунок 99 Рисунок 100
Параболоид
эллиптический с параметрами
![]() и вершиной в начале координат (рисунок
100)
и вершиной в начале координат (рисунок
100)
![]() (65)
(65)
Сечения параболоида
горизонтальными плоскостями
(![]() при
при
![]() ,
,
![]() при
при
![]() )
являются эллипсы:
)
являются эллипсы:
![]() .
.
Сечения параболоида
вертикальными плоскостями
или
являются параболами:
![]() или
или ![]() .
.
Параболоид гиперболический с параметрами и вершиной в начале координат (рисунок 101)
![]() (66)
(66)
Сечения параболоида
горизонтальными плоскостями
представляют собой гиперболы:
![]() .
.
Сечения вертикальными
плоскостями
или
являются параболами:
![]() или
или ![]() .
.
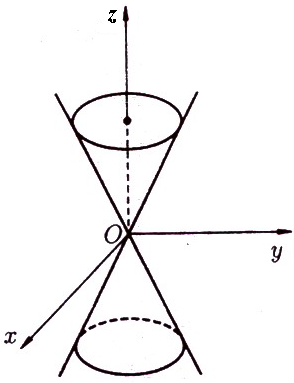
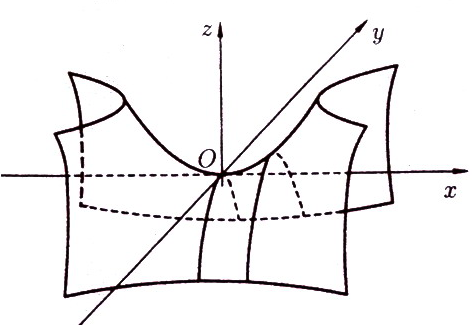
Рисунок 101 Рисунок 102
Конусом называется поверхность, составленная из прямых линий, проходящих через фиксированную точку – вершину конуса. Прямые называются образующими, а линия, которая лежит на конусе, не проходит через вершину и пересекает все образующие, называется направляющей конуса.
Конус эллиптический с вершиной в начале координат и осью (рисунок 102)
![]() (67)
(67)
Если
![]() ,
то конус круглый или круговой.
,
то конус круглый или круговой.
Пересечение конуса
горизонтальными плоскостями
являются эллипсами:
![]() ,
( при
,
( при
![]() эллипс вырождается в точку).
эллипс вырождается в точку).
Сечения конуса
вертикальными плоскостями
или
являются гиперболами:
![]() или
или
![]() при
при
![]() ;
;
или парой
пересекающихся прямых:
![]() ,
,
![]() при
.
при
.
К поверхностям второго порядка относятся цилиндры.
Цилиндры:
Поверхность, которая состоит из прямых линий, параллельных заданному направлению, называется цилиндрической поверхностью или цилиндром, а прямые линии – ее образующими. Линию, лежащую на поверхности и пересекающую все образующие, называют направляющей.
Мы ограничимся
перечислением цилиндров, направляющие
которых расположены в плоскости
![]() ,
а образующие – прямые, параллельные
оси
.
,
а образующие – прямые, параллельные
оси
.
Эллиптический
цилиндр (рисунок 103):
![]() (68)
(68)
Если
![]() ,
то цилиндр круговой
,
то цилиндр круговой
![]() .
.
Гиперболический
цилиндр (рисунок 104):
![]() (69)
(69)
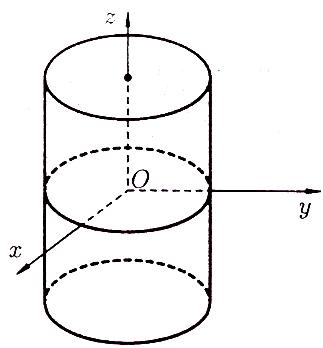
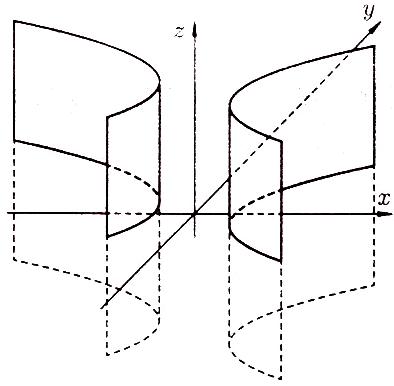
Рисунок 103 Рисунок 104
Параболический
цилиндр (рисунок 105):
![]() (70)
(70)
П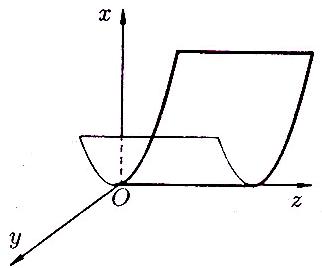 римечание.
Если в каждом из приведенных канонических
уравнений заменить
римечание.
Если в каждом из приведенных канонических
уравнений заменить
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() - фиксированные числа, то новые уравнения
представляют те же поверхности и они
занимают в системе координат
- фиксированные числа, то новые уравнения
представляют те же поверхности и они
занимают в системе координат
![]() такое же положение относительно
плоскостей
такое же положение относительно
плоскостей
![]() ,
,
![]() ,
,
![]() как поверхности, заданные канонически
относительно координатных плоскостей
Рисунок 105
как поверхности, заданные канонически
относительно координатных плоскостей
Рисунок 105
![]() ,
,
![]() ,
,
![]() .
.
Другими словами,
приведенные формулы представляют
параллельный сдвиг поверхности на
вектор
![]() .
.
