Практическое занятие № 4 Взаимное расположение прямой и плоскости
З
адача
1
Найти
точку пересечения прямой и плоскости
и
.
Решение. Рисунок 58
Для того чтобы найти точку пересечения прямой и плоскости необходимо решить систему уравнений. Сначала от канонического уравнения прямой перейдем к параметрическому уравнению
-
параметрическое уравнение прямой. Точка
лежит на прямой и на плоскости,
следовательно, ее координаты удовлетворяют
и уравнению прямой и уравнению плоскости.
Запишем систему линейных уравнений и
решим ее и найдем параметр t.
,
,
Подставив вместо параметра значения в параметрическое уравнения мы получили координаты точки.
Точка
пересечения прямой и плоскости имеет
координаты
.
Ответ.
Задача 2
Доказать,
что прямая
,
,
параллельна плоскости
.
Решение.
.
.
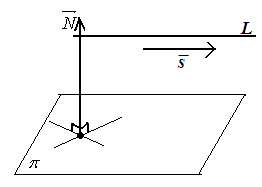Прямая параллельна плоскости , если направляющий вектор прямой перпендикулярен
Рисунок 59 нормальному вектору плоскости .
.
прямая
параллельна плоскости.
Задача
3
Найти величину угла между прямой
,
,
,
и плоскостью
.
Решение.
Угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость.
.
Угол
между прямой
и
плоскостью
:
определяется по формуле
.
Рисунок 60
.
.
,
.
Ответ.
Задача
4
При каких значениях
и
прямая
лежит в плоскости
?
Решение. Для прямой, которая задана каноническим уравнением
известен
направляющий вектор и точка принадлежащая
ей, с координатами
.
Для плоскости известен нормальный
вектор
.
Прямая
лежит в плоскости, если выполняются
Рисунок 61 два
условия: 1)
и
2)
точка
лежит в плоскости
,
т.е.
Ответ.
Задача 5 Установить взаимное расположение прямой и плоскости:
а)
и 
;
б)
и 
.
Решение.
а)
Имеем, направляющий вектор прямой задан
координатами
,
нормальный вектор плоскости задается
координатами
.
Как видно координаты направляющего
вектора
прямой и нормального вектора
плоскости не пропорциональны: прямая
не перпендикулярна плоскости
.
Найдем значение выражения
:
.
Условие параллельности прямой и плоскости не выполняется. Значит, прямая пересекает плоскость.
б)
Здесь, вектора направляющий и нормальный
заданы координатами и точка лежащая
на прямой
,
,
,проверим
равенство
.
Следовательно, данная прямая параллельна
плоскости или лежит на ней. Проверим
условия
принадлежности прямой плоскости:
.
Условия выполняются, поэтому прямая лежит в плоскости.
Домашнее задание № 4
Составить уравнение плоскости, проходящей через точку
перпендикулярно прямой
.
Ответ.
Найти координаты точки пересечения прямой
с плоскостью
.
Ответ.
Найти расстояние между прямыми
и
.
Ответ. 7
а) При каком значении
прямая
параллельна плоскости
.
б)
При каком значении
прямая
параллельна плоскости
.
в)
При каком значении
прямая
,
,
параллельна плоскости
.
Ответ.
а)
; б)
; в)
При каких значениях
и
прямая
,
,
лежит в плоскости
.
Ответ.
а) При каких значениях и плоскость
перпендикулярна к прямой
б)
При каких значениях
и
прямая
перпендикулярна к плоскости
.
в)
При каких значениях
и
прямая
,
,
перпендикулярна плоскости
.
Ответ.
а)
; б)
; в)
.
Найти проекцию точки
на плоскость
.
Ответ.
Найти точку, симметричную точке
относительно плоскости
.
Ответ.
Вычислить расстояние
от точки
до прямой
.
Ответ.
