Практическое занятие № 1 Уравнение прямой. Способы задания прямой. Взаимное расположение прямых

Задача 1 Построить и составить уравнение прямой :

а) , ; б) , ;

в) , ; г) , ;

д) , ; е) т. , ;

ж) проходящей через 2 различные точки и ;

з) проходящей через точку перпендикулярно прямой , проходящей через точки и , где , ;

и) проходящей точка параллельно прямой , проходящей через точки и , где , ;

к) проходящей через точку и направляющий вектор ;

л) проходящей через точку с нормальным вектором .

Р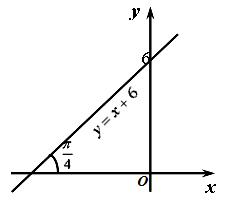 ешение. а) Так как ( - ордината точки пересечения прямой с осью ) и ( - угол, который прямая образует с положительным направлением оси ). Воспользуемся формулой уравнением прямой с угловым коэффициентом .

,

.

Ответ. Рисунок 18

б ) Так как ( - ордината точки пересечения прямой с осью ) и ( - угол, который прямая образует с положительным направлением оси ). Воспользуемся формулой уравнением прямой с угловым коэффициентом .

,

.

Ответ. Рисунок 19

в) Так как ( - расстояние, которое отсекает прямая на оси ) и , т.е. прямая перпендикулярно оси .

Ответ. Рисунок 20

г) Так как , . Воспользуемся формулой уравнением прямой с угловым коэффициентом .

.

Ответ. Рисунок 21

д) Так как , ( - угловой коэффициент прямой). Воспользуемся формулой уравнением прямой с угловым коэффициентом

.

2 3

O

Ответ. Рисунок 22

е) Так как дана точка лежащая на прямой и угловой коэффициент , воспользуемся формулой

, ,

.

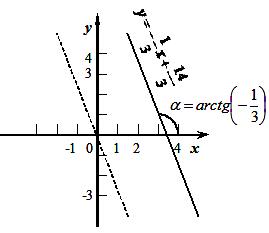Ответ. Рисунок 23

ж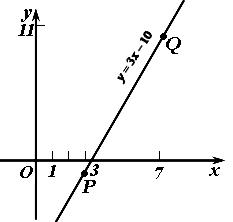 ) Уравнение прямой, проходящей через две различные точки и выглядит следующим образом:

.

Рисунок 24

.

Ответ.

з) Уравнение прямой, проходящей через т. перпендикулярно прямой , где , выглядит следующим образом:

Составим уравнение прямой :

.

.

У равнение : . Угловой коэффициент прямой : . Так как прямые перпендикулярны, то их угловые коэффициенты противоположны по знаку и обратны по значению, т.е. . Воспользуемся формулой .

Ответ. Рисунок 25

и) Уравнение прямой составили в предыдущем примере : .

Так как по условию две прямые параллельны, то их угловые коэффициенты равны, т.е. угловой коэффициент для нашей прямой будет тоже равен 2.

,

.

Ответ. Рисунок 26

к) Уравнение прямой, проходящей через точку и направляющий вектор задается уравнением: .

Ответ. Рисунок 27

л ) Общее уравнение прямой, проходящей через точку с нормальным вектором , выглядит следующим образом: . Таким образом, уравнение прямой, проходящей через т. с нормальным вектором , будет следующим:

,

.

Ответ. Рисунок 28

Задача 2 Определить взаимное расположение прямых:

а) , ; б) , ;

в) , , г) , .

Решение. а) , .

1 способ. Найдем угол между двумя прямыми, если прямые заданы через угловые коэффициенты. От общего уравнения прямой

п ерейдем к уравнению прямой через угловой коэффициент

и воспользуемся формулой

2 способ. Найдем угол между двумя прямыми, если прямые заданы в общем виде: .

, Воспользуемся формулой .

Ответ.

б) , .

1 способ. Аналогично, от общего уравнения прямой

перейдем к уравнению прямой через угловой коэффициент : . Угловые коэффициенты противоположны по знаку и обратны по значению или . Следовательно, прямые перпендикулярны, т.е. угол между ними .

2 способ. Прямые заданы в общем виде . Найдем скалярное произведение векторов и : нормальные вектора и перпендикулярны прямые пересекаются под углом .

Ответ.

в) , .

1 способ. Прямые заданы в общем виде , . Перейдем от общего уравнения прямой _{к уравнению прямой через угловой коэффициент}

_{и найдем угловые коэффициенты прямых}

Угловые коэффициенты равны, т.е.

следовательно, прямые параллельны.

2 способ. Так как прямые заданы в общем виде , то запишем координаты нормальных векторов и : . Так как координаты векторов и пропорциональны, то вектора коллинеарны .

Нормальные вектора коллинеарны, следовательно, прямые параллельны.

Ответ. Прямые параллельны

г) , .

1 способ. Перейдем от общего уравнения прямой

_{к уравнению прямой через угловой коэффициент и найдем угловые коэффициенты прямых}

, ; ,

Следовательно, прямые совпадают, так как и .

2 способ. Так как прямые заданы в общем виде , то запишем координаты нормальных векторов и : . Так как координаты векторов и пропорциональны и отношение свободных членов тоже равно , т. е. . Таким образом, справедлива формула прямые совпадают.

Ответ. Прямые совпадают

Задача 3 При каких значениях и две прямые ,

а) параллельны;

б) совпадают;

в) имеют общую точку.

Решение. Прямые на плоскости могут быть либо параллельными, т.е. ; либо совпадать ; либо пересекаться

а) ,

. ;. .

б) прямые совпадают тогда и только тогда, когда .

в) При и прямые имеют общую точку.

Ответ. а) при и прямые параллельны;

б) при и прямые совпадают;

в) при и прямые имеют общую точку

Задача 4 Привести общее уравнение прямой к нормальному виду:

а) ; б) ; в) .

Р ешение. а) Прямая задана в общем виде Приведем к нормальному виду Найдем нормирующий множитель . Так как , то . Умножим общее уравнение на нормирующий множитель .

б) ,

Так как , то : .

в) , . Так как , то : , .

Ответ. а) ; б) ; в)

Задача 5 Вычислить расстояние между прямыми:

а) , ; б) , .

Решение. а)Исследуем данные прямые как они расположены друг относительно друга , , .

Так как прямые параллельны. Найдем расстояние между параллельными прямыми. На прямой найдем точку; пусть , тогда . Точка .

По формуле , найдем расстояние от точки , т.е. до прямой , т.е. .

.

б) Исследуем расположение данных прямых и .

, ,

Используя формулу

получим Следовательно, прямые совпадают _{и расстояние между ними равно нулю ( )}.

Ответ. а) ; б)

Задача 6 При каких значениях следующие пары прямых и : а) параллельны; б) перпендикулярны: : и : ;

Решение. 1 способ. а) и .

Две прямые и параллельны ( ), если нормальные вектора и коллинеарны. , .

б) Если две прямые и перпендикулярны ( ), то нормальные вектора и ортогональны : , , .

2 способ. Запишем уравнения прямых через угловые коэффициенты.

а) , и ,

Прямые , если угловые коэффициенты прямых равны. Приравняем угловые коэффициенты прямых .

б) Используем признак перпендикулярности двух прямых, если прямые заданы в общем виде. Прямые перпендикулярны, если угловые коэффициенты прямых противоположны по знаку и обратны по значению ,

Ответ. а) 4; б)

Задача 7 Через точку пересечения прямых , проведена прямая, параллельная прямой .

Решение. Найдем точку пересечения прямых и . Решим систему линейных уравнений

Точка пересечения двух прямых . Так как прямые параллельны, то нормальные вектора коллинеарны: .

- уравнение прямой, проходящей через точку с нормальным вектором .

Ответ.

Задача 8 Найти координаты точки , симметричной точке относительно прямой .

Рисунок 29

Решение. Найдем уравнение прямой , проходящей через точку и перпендикулярной данной прямой по формуле : , .

Так как точка лежит на , то ее координаты удовлетворяют уравнению , т.е. .

Найдем расстояние от точки до прямой .

.

Найдем точку пересечения двух прямых:

.

Точка .

Найдем расстояние , которое равно :

.

Решим систему уравнений:

,

,

Ответ.

Задача 9 Определить при каком значении три прямые , , будут пересекаться в одной точке.

Решение. Для того, чтобы найти при каком значении три прямые будут пересекаться в одной точке, необходимо решить систему уравнений:

Ответ.