24. Анализ ресурсов.

Предположим, что для некоторых значений А, b и с найден оптимальный план х^*, максимизирующий суммарный доход . Достаточно естественным представляется вопрос: как будет изменяться оптимальный план х* при изменении компонент вектора ограничений b и, в частности, при каких вариациях b оптимальный план х* останется неизменным? Данная задача получила название проблемы устойчивости оптимального плана. Очевидно, что исследование устойчивости х* имеет и непосредственное практическое значение, так как в реальном производстве объемы доступных ресурсов b_i могут существенно колебаться после принятия планового решения х^* .

Когда вектор ограничений b изменяется на ∆b или, как еще говорят, получает приращение ∆b, то возникают соответствующие вариации для оптимального плана и значения целевой функции . Допустим, приращение ∆b таково, что оно не приводит к изменению оптимального базиса задачи, т. е. . Определим функцию F(b), возвращающую оптимальное значение целевой функции задачи для различных значений вектора ограничений b (1.55)

Рассмотрим отношение ее приращения к при-

ращению аргумента ∆b. Если для некоторого i устремить , то мы получим 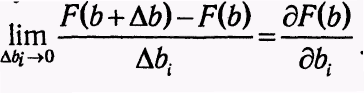(1.56)

Учитывая, что в соответствии с теоремой 1.5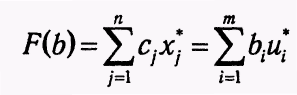 (1.57) и подставив (1.57) в (1.56), приходим к выражению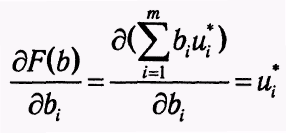 (1.58)Из формулы (1.58) вытекает экономическая интерпретация оптимальных переменных двойственной задачи. Каждый элемент u_i^* может рассматриваться как предельная (мгновенная) оценка вклада г-го ресурса в суммарный доход F при оптимальном решении х*. Грубо говоря, величина и* равна приросту дохода, возникающему при увеличении ресурса i на единицу при условии оптимального использования ресурсов.

В различных источниках компоненты оптимального плана двойственной задачи также называются двойственными оценками или теневыми ценами, а Л. В. Канторович предлагал такой термин, как объективно обусловленные оценки.

На основе теорем двойственности для пары задач ЛП в общей форме могут быть сформулированы некоторые важные (с точки зрения экономической интерпретации) следствия.

Если при использовании оптимального плана прямой задачи i-e ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей двойственной переменной равно нулю, т. е. если

В рамках рассматриваемой задачи производственного планирования это означает, что если некоторый ресурс b_i имеется в избыточном количестве (не используется полностью при реализации оптимального плана), то i-e ограничение становится несущественным и оценка такого ресурса равна 0.

Если при использовании оптимального плана двойственной задачи j-e ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей переменной прямой задачи должно быть равно нулю, т. е. если

Учитывая экономическое содержание двойственных оценок , выражение может быть интерпретировано как удельные затраты на j-й технологический процесс. Следовательно, если эти затраты превышают прибыль от реализации единицы j-го продукта, то производство j-го продукта является нерентабельным и не должно присутствовать в оптимальном производственном плане (х* = 0).