Тема 3. Приближенное интегрирование.

1. Постановка задачи. Формулы Ньютона-Котеса.

В технических задачах часто встает необходимость интегрирования. Речь идет о вычислении интеграла J= (x)dx (1). Если известна первообразная F(x), то J=F(b)-F(a) (формула Ньютона-Лейбница). Однако, если вид F(x) неизвестен (или задан таблицей) или сложен, необходимо воспользоваться численными методами. Численное вычисление интеграла называется механической квадратурой, а формулы вычисления – квадратурными. Обычный прием квадратурной формулы состоит в том, что подынтегральная функция f(x) заменяется какой-либо аппроксимирующей функцией более простого вида, например, рядом Тейлора, рядом Фурье или интерполяционным полиномом (в форме Лагранжа или Ньютона). Чаще всего эта функция заменяется интерполяционным полиномом. (x)dx= _n(x)dx+R (2). Результат будет достаточно точным, если полином L_n(x) хорошо приближает функцию f(x), т. е. если функция f(x) достаточно гладкая.

_n(x)dx= •y_idx= •y_idx= _iy_i.

Таким образом, (x)dx= _iy_i+R (3), где A_i= dx.

Интерполяционная формула с равноотстоящими узлами была рассмотрена Ньютоном, а Котес вычислил коэффициенты A_i для i от 1 до 10. Поэтому формула (3) называется формулой Ньютона-Котеса.

2. Формулы прямоугольников.

Вывод квадратурных формул можно получить из наглядных геометрических соображений. Известно, что (x)dx= (ξ_i)•Δx_i (4) при max(Δx_i)→0; ξ_iΔx_i.

Предел не зависит от способа разбиения отрезка (a; b) на промежутки Δx_i и выбора точек ξ_i из этих промежутков. Следовательно, если разбить отрезок (a, b) на достаточное число малых отрезков, то можно ожидать, что интегральная сумма будет с какой-то точностью приближать значения интеграла.

(x)dx= (ξ_i)•Δx_i+R (5).

Обычно Δx_i выбирают равными, т. е. делят отрезок (a; b) узлами a₀, a₁…a_n такими, что x_i+1-x_i=h= . Точку ξ_i можно брать справа, посередине или слева на отрезке Δx_i. ξ_i=x₀+ih – слева; ξ_i=x₀+ih+ – в центре; ξ_i=x₀+(i+1)h – справа. Полученные при этом из формулы (5) формулы называются соответственно формулами левых (J=h (x₀+ih)+R_л (6.2)), центральных (J=h (x₀+ih+ )+R_ц (6.3)) и правых (J=h (x₀+ih)+R_п (6.3)) прямоугольников. Таким образом, площадь под графиком функции заменяется площадью ступенчатой фигуры, состоящей из прямоугольников.

Остаточные члены формул прямоугольников.

Очевидно, что формулы прямоугольников – случай, когда подынтегральная функция заменяется интерполяционными полиномами Ньютона нулевого порядка.

P_n(x)=y₀+ •(x-x₀)+… При n=0 P₀=y₀.

(x)dx≈ ₀(x)dx= ₀(x)dx=(x₁-x₀)•y₀

r_л=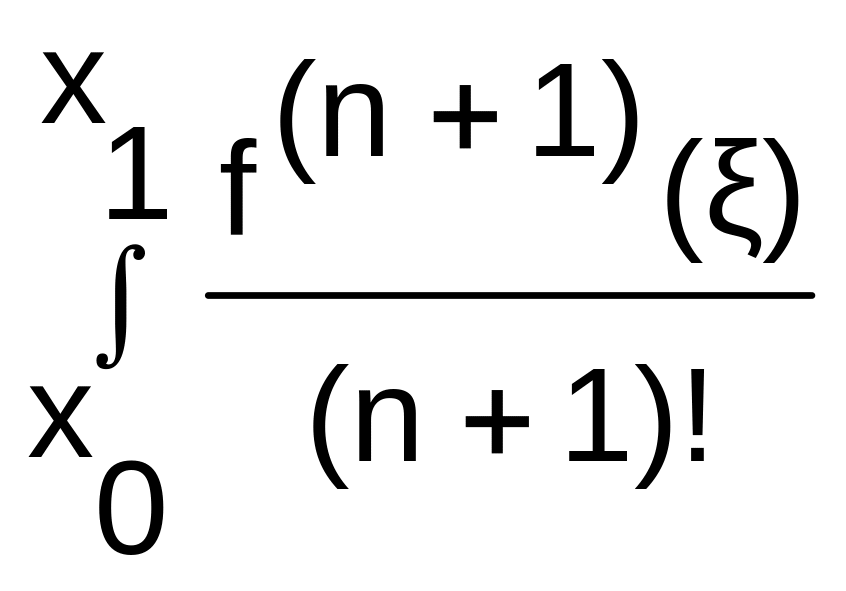 •ω(x)dx=f⁽⁰⁺¹⁾(ξ)• 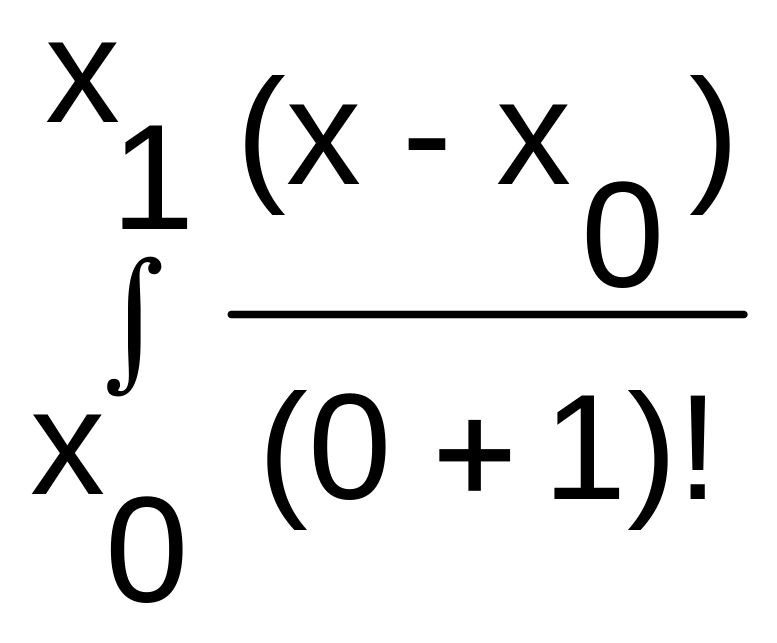dx=f'(ξ)( -x₀x = •f'(ξ)=f'(ξ)•

R_л=r_л•n= •h•f'(ξ) (7.1)

r_п=-f'(ξ)•

R_п=- •h•f'(ξ) (7.3)

r_ц=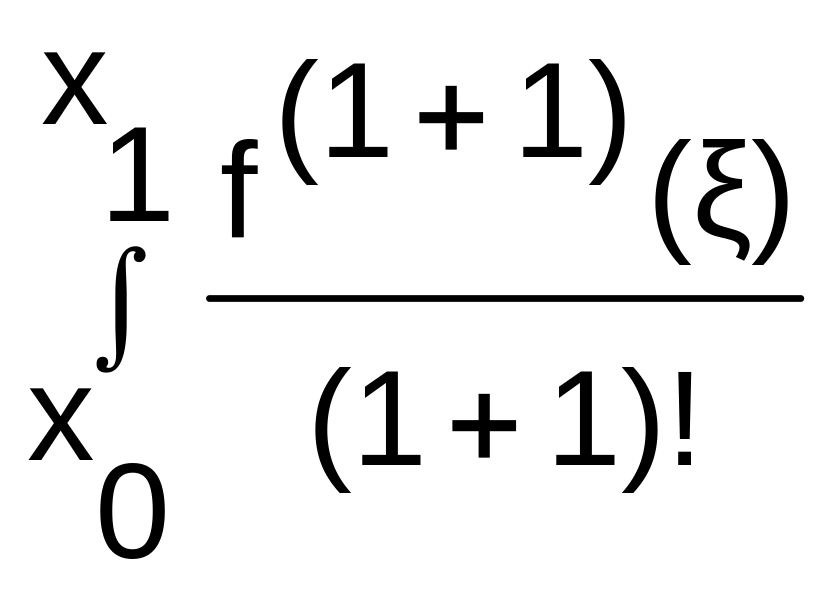 •(x-x₀)•(x-(x₀+ ))dx= = • •(t- )dt= × ×( - • )= •h³

R_ц= •h²•f''(ξ) (7.2)

Методы недостаточно хороши с точки зрения точности, требуют большого числа точек разбиения и кроме метода прямоугольников не применяются.

3. Формула трапеций и ее остаточный член.

Рассмотрим случай, когда степень интерполяционного полинома равна единице, т. е. n=1

P₁(x)=y0+ •(x-x₀)=y₀+ •(x-x₀).

(x)dx≈ ₁(x)dx=(x₁-x₀)•y₀+ •( -xx₀ =y₀h+ •( -x₀x₁- +x₀²)=y₀h+ • = =y₀h+ •h= •(y₀+y₁).

(x)dx≈ •(f(x₀)+f(x₁)) (8)

Если рассматривать n отрезков, то (x)dx≈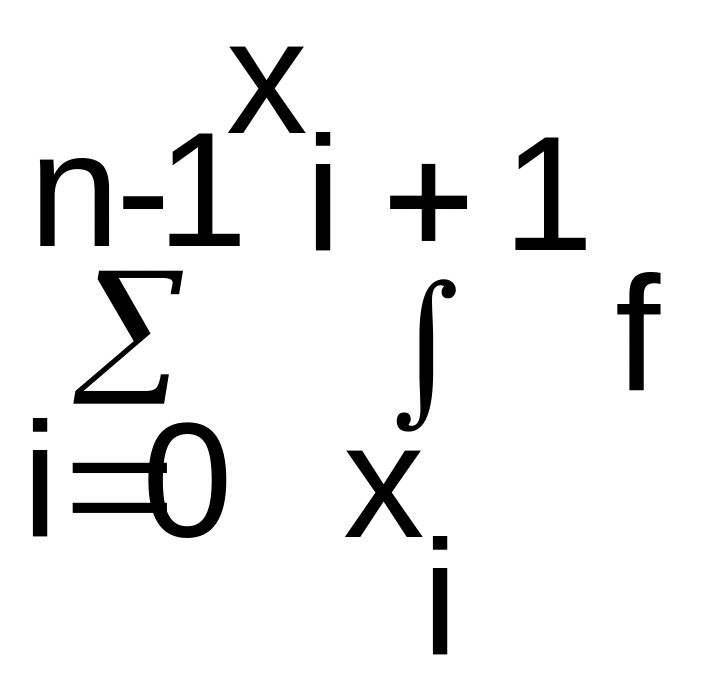 (x)dx= •(f(x_i)+f(x_i+1))= •(f(x₀)+f(x₁)+f(x₁)+f(x₂)+…+f(x_n-1)+f(x_n))= •(f(a)+f(b)+2 (x_i)) (10).

Оценка погрешности для формулы трапеций.

r_т=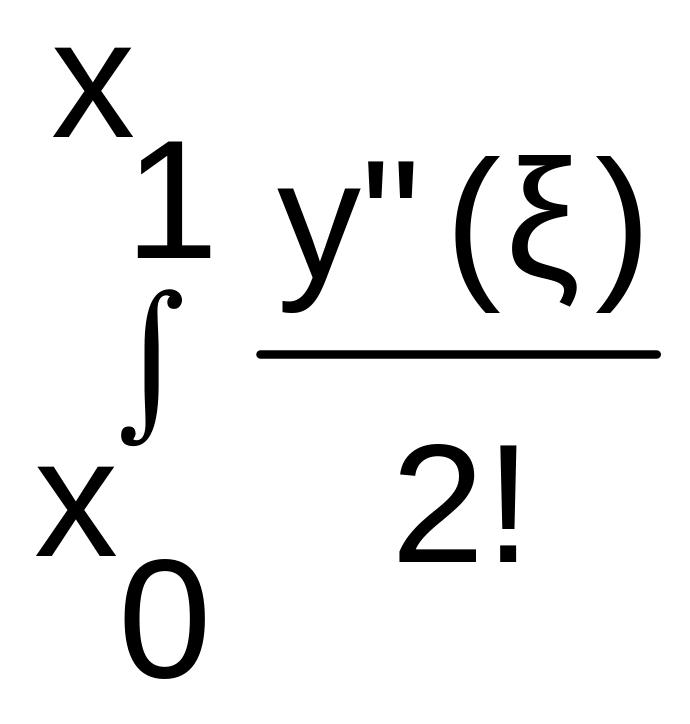 •(x-x₀)•(x-x₁)dx= = • •(t-h)dt= •( - •h)= •h³

R_т=r_т•n= •h²•f''(ξ) (11).

Очевидно, что при этом подынтегральная функция заменяется кусочно-линейной функцией.

4. Формула Симпсона и ее остаточный член.

Рассмотрим случай, когда степень интерполяционного полинома равна двум.

P₂(x)=y0+ •(x-x₀)+ •(x-x₀)•(x-x₁)=y₀+ •(x-x₀)+ •((x-x₀)²-(x-x₀)•h)

(x)dx≈ y0+ •(x-x₀)+ •((x-x₀)²-(x-x₀)•h))= = = y0+ •t+ •(t²-t•h))=2hy₀+ • + • + • •h=2hy₀+2hΔy₀+ •hΔ²y₀=

= •h•(6y₀+6y₁-6y₀+y₂-2y₁+y₀)= •h•(y₂+4y₁+y₀) (12).

Если рассматривать n отрезков, то (x)dx≈ h•(f(x₀)+f(x_n)+4 (x_i)+2 (x_i)) (13).

Остаточный член формулы (12) r_с=- •y⁽⁴⁾(ξ). Очевидно, что полиномы до третьей степени включительно интегрируются точно.

Rс=- •h⁴•f⁽⁴⁾(ξ).

5. Автоматический выбор шага в квадратурных формулах.

Т. к. в большинстве случаев задается не количество разбиений n отрезка (a; b), а погрешность ε, то вычисления проводятся по алгоритму так называемого двойного пересчета. Это означает, что интеграл считается с некоторым количеством разбиений, затем количество разбиений удваивается и снова считается интеграл. Если значения отличаются менее чем на погрешность, значит, интеграл посчитан с заданной точностью. Однако, по этому алгоритму вычисления некоторых значений функции будет производиться многократно, что нерационально. Обычно при вычислении интеграла с новым количеством отрезков использую результаты предыдущих вычислений (кроме метода центральных прямоугольников).

В теории, зависимость погрешности вычисления от количества разбиений должна асимптотически приближаться к нулю при увеличении количества разбиений. Скорость приближения зависит от метода. На практике после некоторого количества разбиений погрешность не уменьшается, а увеличивается, т. к. сказывается вычислительная погрешность.