1. Что называется матрицей?

Это таблица чисел состоящая из m строк и n столбцов.

2. Что называется размером матрицы?

Количество строк и столбцов.

3. В каком месте матрицы А = (a_ij) находятся её элементы а₃₄?

В 3 строке, 4 столбце.

4. Какая матрица называется квадратной?

Если число строк равно числу столбцов m = n.

1. Что называется порядком матрицы?

Число n или m.

2. Могут ли быть равными две квадратные матрицы, одна из которых – четвёртого порядка, а другая – пятого?

Нет т.к. их стоящие элементы на одинаковых местах не равны.

3. Какие элементы квадратной матрицы называются диагональными?

Если номер строки равен номеру столбца.

4. Какая матрица называется диагональной?

Если все недиагональные элементы равны 0.

5. Какие матрицы называются равными?

Это элементы А и В стоящие на равных местах.

6. Какая матрица называется нулевой?

Если все её элементы равны 0.

7. какая матрица называется единичной?

Если все элементы главной диагонали равны 1.

8. Какие элементы стоят на главной диагонали единичной матрицы?

1

9. Может ли единичная матрица быть прямоугольной?

Нет т.к. не все элементы главной диагонали будут равны 1.

10. Сформулировать определение операции транспонирование матриц.

Замена каждой её строки столбцом, с тем же номером.

11. Каков размер матрицы, транспонированной к матрице размера m х n

n х m

16. Какая матрица получается при транспонировании матрицы – строки?

Матрица столбец.

17. Какая матрица получается при транспонировании матрицы – столбца?

Матрица строка.

18. Сформулировать определение операции сложение матриц.

Суммой двух матриц А = (а_ij) и В = (b_ij) одинаковой размерности, называется матрица C = (c_ij) с той же размерности, каждый элемент c_ij который равен сумме элементов a_ij + b_ij стоящих на одинаковых местах в слагаемых матрицах А и В.

19. Какие матрицы можно складывать?

Одинаковой размерности.

20. Можно ли найти сумму квадратной матрицы четвёртого порядка и матрицы размера 6 х 7?

4 х 4, 6 х 7, нет т.к. они разной размерности.

21. Сформулировать определение операции умножение матрицы на число.

22. Перечислить свойства операции сложение матриц.

• А+В = В+А, для любых матриц А и В

• (А+В) + С = А+(В+С) для любых матриц А,В,С.

• Если 0 – нулевая матрица, то А+0 = 0+А = А, для любой матрицы А.

• (А+В)^т = А^т+В^т, для любых матриц А и В.

23. Перечислить свойства операции умножения матрицы на число.

1.(LB)A=L(BA)

2.(L+B)A=LA+BA

3.L(A+B)=LA+LB

4. =

24. Перечислить свойства операции умножения матриц.

1. A*(BC)=(AB)*C

2.L*(AB)=(LA)*B=A*(LB)

3.(A+B)*C=AC+BC

4. =

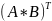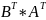
25. Какие две матрицы называются перестановочными?

Если А*В = В*А, то матрицы А и В называются перестановочными.

26. Чему равно произведение любой матрицы на единичную матрицу?

А*Е = Е*А = А существует, как А*Е так и Е*А, получим матрицу А.

27. Коммутативна ли операция умножения матриц?

Операция матриц некоммутативна, т.е. если существует произведение А*В, то В*А может вообще не существовать, из-за несовпадения размерностей.

28. Можно ли умножить матрицу 3 х 7 на матрицу 7 х 5

Да, т.к. число столбцов первой матрицы равно числу строк другой матрицы.

29. Можно ли умножить матрицу размера 4 х 6 на матрицу размера 4 х 8?

Нет, т.к. число столбцов первой матрицы несовпадает с числом строк другой матрицы.

30. Каков размер матрицы, являющейся произведением матрицы размера 12 х 9 на матрицу размера 9 х 5?

12 х 5.

31. Пусть А

32. Сформулировать признаки равенства определителя нулю.

• Определитель, содержащий две одинаковые строки, равен нулю.

• Если одна из строк определителя целиком состоит из нулей, то определитель равен нулю.

• Определитель, содержащий две пропорциональные строки, равен нулю.

• Если одна из строк определителя является линейной комбинацией его других строк, то определитель равен нулю.

33. При каких условиях определитель матрицы второго порядка равен нулю?

При всех, кроме определителя который является линейной комбинацией.

34. Перечислить преобразования определителя, не меняющие его значения.

• Определитель не изменяется при транспонировании.

• Определитель не изменяется, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

35. Сформулировать определение минора элемента определителя.

Минором элемента а_ij определителя квадратной матрицы n-го порядка, называется определитель (n – 1) – го порядка, полученный из данного вычеркиванием i – ой и j – го столбца, на пересечение которых стоит выбранный элемент.

36. Как можно получить из матрицы А = а_ij минор М₃₇?

Вычеркнуть 3 – строку, 7 – столбец.

37. Сформулировать определение алгебраического дополнения элемента определителя.

Алгебраическим дополнением определителя называется его минор взятый со знаком

(-1) ^i+j

38. Чем отличается минор М₈₅ от алгебраического дополнения А₈₅?

Отличается знаком, т.к. сумма строки и столбца, число нечётное.

39. Чем отличается Минор М₂₆ от алгебраического дополнения А₂₆?

Не чем не отличается, т.к. сумма строки и столбца чётное.

40. Сформулировать теорему о разложении определителя.

Теорема. (О разложении определителя.)

Определитель равен сумме произведений элементов любой строки (или любого столбца) определителя на их алгебраические дополнения:

,  ;       (1)

или

,  .       (2)

41. Чему равна сумма произведений элементов любой строки (столбца) определителя на их алгебраические дополнения?

Нулю.

42. Чему равна сумма произведений элементов любой строки (столбца) определителя на их алгебраические дополнения соответствующих элементов другой строки (столбца)?

43. Какая матрица называется вырожденной?

Если её определитель равен нулю.

44. Какая матрица называется невырожденной?

Если её определитель отличен от нуля.

45. Сформулировать определение обратной матрицы.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

46. Сформулировать теорему об определителе произведения матриц.

47. Как можно находить определитель произведения квадратных матриц.

48. Сформулировать теорему об обратной матрице.

Обратная матрица А^-1 существует тогда и только тогда, когда исходная матрица невырожденная

49. Сформулировать практический способ нахождения обратной матрицы.

Алгоритм нахождения обратной матрицы.

1. Вычисляем определитель матрицы. Если он равен нулю, то обратная матрица не существует.

2. Если определитель отличен от нуля, то находим алгебраические дополнения для всех элементов матрицы.

3. Строим присоединенную матрицу транспонированных алгебраических дополнений.

4. Каждый элемент полученной матрицы делим на определитель исходной.

50. Каков вид обратной матрицы?

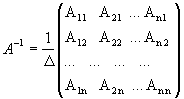
51. Какое условие должно выполняться, чтобы матрица имела себе обратную матрицу?

Она должна быть невырожденной и квадратной.

52. Имеет ли прямоугольная матрица себе обратную матрицу?

Нет

53. Имеет ли вырожденная матрица себе обратную матрицу?

Нет

54. Сколько обратных матриц может иметь данная матрица?

1

55. Сформулировать определение ступенчатой матрицы.

Ступенчатая матрица — матрица, имеющая m строк, у которой первые r диагональных элементов ненулевые, r ≤ m, а элементы, лежащие ниже диагонали и элементы последних m − r строк равны нулю:

56. Может ли ступенчатая матрица содержать нулевые строки?

Нет

57. Какова высота каждой ступеньки ступенчатой матрицы?

1 – строка.

58. Что называется шириной ступеньки ступенчатой матрицы?

Число элементов строки стоящие на ступеньке.

59. Будет ли нулевая матрица ступенчатой?

Нет, т.к. все элементы равны нулю.

60. Будет ли единичная матрица ступенчатой?

Да.

61. Какие элементарные преобразования строк вы знаете?(в тетради)

62. Сформулировать алгоритм приведения произвольной матрицы к ступенчатому виду.

63. Сформулировать определение минора порядка k матрицы.

Определитель квадратной матрицы порядка k, получаемой из матрицы А вычеркиванием каких-либо строк или столбцов.

64. Что называется рангом матрицы?

Называется наивысший порядок отличных от нулевых миноров этой матрицы.

65. Пусть минор порядка 9 некоторой матрицы отличен от нуля.

9

66. Матрица А имеет размер 5 х 7. Какое наибольшее значение может принимать ранг этой матрицы?

5

67. Чему равен ранг нулевой матрицы?

Равен 0.

68. Когда ранг матрицы равен нулю?

Если все элементы равны нулю.

69. Чему равен ранг квадратной невырожденной матрицы пятого порядка?

5

70. Изменится ли ранг матрицы при элементарных преобразованиях её строк или столбцов?

Не изменится.

71. Как найти ранг ступенчатой матрицы?

• Привести к ступенчатому виду.

• Вычислить ранг полученной ступенчатой матрицы сосчитав количество строк.

72. Сформулировать алгоритм нахождения ранга матрицы.

73. Какой минор называется базисным минором матрицы?

Любой ненулевой минор матрицы, порядок которого совпадает с рангом данной матрицы.

74.76. Какие строки матрицы называются линейно зависимыми?

Столбцы матрицы е₁, е₂, е₃ называются линейно зависимыми, если существуют такие числа к₁, к₂, к₃, не равные нулю одновременно.

75.77. Какие строки матрицы называются линейно независимыми?

Столбцы матрицы е₁, е₂…е_s называются линейно независимыми, если линейная комбинация этих столбцов равна нулю только при нулевом наборе коэффициентов.

78. Что можно сказать про строки матрицы, элементы которых входят в её базисный минор?

Они линейно независимы.

79. Что можно сказать про столбцы матрицы, элементы которых входят в её базисный минор?

Они линейно независимы.

80. Какой вид имеет система линейных алгебраических уравнений?

Система линейных уравнений с n неизвестными х₁, х₂…х_n называется система вида, где а_ij, b₁ (i = 1, m; j = 1, n) произвольные числа, называемые соответственно коэффициентами при неизвестных и собственными членами уравнений.

81. Какая матрица называется матрицей системы?

Коэффициент при неизвестных образует прямоугольную таблицу, которая называется матрицей системы.

82. Какая матрица называется расширенной матрицей системы?

Это матрица, которая получается приписыванием к ней справа столбца свободных членов.

83. Сформулировать определение решения системы линейных алгебраических уравнений.

Решением системы называется упорядоченный набор ( к₁, к₂….к_n), из которых может быть получено любое конкретное решение системы, называется её общим решением.

84. Какая система линейных алгебраических уравнений называется совместной?

Система имеющая хотя бы одно решение.

85. Какая система алгебраических уравнений называется несовместной?

Система не имеющая ни одного решения.

86. Какая система линейных алгебраических уравнений называется определённой?

Система имеющая одно решение.

87. Какая система линейных алгебраических уравнений называется неопределённой?

Система имеющая более одного решения.

88. Какая система линейных алгебраических уравнений называется однородной?

Если все свободные члены равны нулю.

89. Какая система линейных алгебраических уравнений называется неоднородной?

Если все свободные члены не равны нулю.

90. Что называется общим решением системы линейных алгебраических уравнений?

Выражение для неизвестных из которого может быть получено любое конкретное решение.

91. Что называется частным решением системы линейных алгебраических уравнений?

Любое конкретное решение системы.

92. Какие две системы линейных алгебраических уравнений называются равносильными или эквивалентными?

Системы уравнений имеющие одно и то же множество решений.

93. При каких условиях система линейных алгебраических уравнений имеет единственное решение?

Если число ступенек равно числу неизвестных последовательностей, ступенька равна 2 шага в ширину.

94. В какой системе линейных алгебраических уравнений применим метод обратной матрицы?

Число уравнений равно числу неизвестных матрица А невырожденная.

95. Сформулировать суть метода Гаусса решения линейных систем.

Суть метода Гаусса состоит в том, что с помощью некоторых операций исходную систему уравнений можно свести к более простой системе. Эта простая система имеет треугольный вид:

a11x1 +	a12x2 +	a13x3 +	...	a1NxN = b1
	a22x2 +	a23x3 +	...	a2NxN = b2
		a33x3 +	...	a3NxN = b3
...
			...	aNNxN = bN

Особенность этой системы - в строках с номером i все коэффициенты a_ij при j<i равны нулю.

96. Сформулировать теорему Крамера.

Если главный определитель системы n линейных уравнений отличен от 0 , то система совместна и имеет единственное решение.

97. К какой системе линейных алгебраических уравнений применимо правило Крамера?

К невырожденной.

98. При каких условиях система алгебраических уравнений, определяемая ступенчатой матрицей, несовместна?

Система несовместна, если последняя ступенька матрицы имеет только один шаг в ширину.

99. При каких условиях система алгебраических уравнений, определяемая ступенчатой матрицей. совместна?

 Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

100. При каких условиях система алгебраических уравнений, определяемая ступенчатой матрицей, имеет единственное решение?

Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение

101. При каких условиях система алгебраических уравнений, определяемая ступенчатой матрицей, имеет бесконечно много решений.

Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

102. Чему равно количество базисных неизвестных для системы линейных алгебраических уравнений, определяемой ступенчатой матрицей?

x₁ , x₂ , ..., x_r

103. Чему равно количество свободных неизвестных для системы линейных алгебраических уравнений, определяемой ступенчатой матрицей?

x_r+1 , x_r+2 , ..., x_n

104. Будет ли нулевым решение системы линейных алгебраических уравнений, в которой все свободные неизвестные равны нулю?

Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные  равны нулю

105. В чем состоит суть частного способа решения матричных уравнений?

106. В чем состоит суть общего способа решения матричных уравнений?

107. Сформулировать теорему Кронекера-Капелли.

Система линейных алгебраических уравнений (1) совместна тогда и только тогда, когда ранг расширенной матрицы А системы равен рангу матрицы системы А.

108. Как совместность неоднородной системы линейных алгебраических уравнений связана с рангом матрицы системы и рангом её расширенной матрицы?

109. Как количество решений совместной неоднородной системы линейных алгебраических уравнений связано с рангом её матрицы и количеством неизвестных?

110. Какая система является базисной подсистемой для данной системы линейных алгебраических уравнений?

Совместная, однородная в которой количество переменных больше её ранга.

111. Какие неизвестные системы линейных алгебраических уравнений является базисными и свободными?

• Базисные неизвестные – это неизвестные, коэффициенты при которых входят в базисный минор матрицы системы.

• Свободные неизвестные – это неизвестные, коэффициенты при которых НЕвходят в базисный минор матрицы системы.

112. Сформулировать определение фундаментальной системы решений.

Любые n – r линейно независимых решений однородной системы СЛАУ, называют её ФСР.

113. Сформулировать определение нормальной фундаментальной системы решений.

Это ФСР однородной системы СЛАУ, в которой свободные неизвестные задаются по формулам:

114. Перечислить свойства решений однородной системы линейных алгебраических уравнений.

• Любое решение однородной СЛАУ, умноженное на любое число, также является решением этой системы.

• Сумма решений однородной СЛАУ также является её решением.

115. Какова структура общего решения однородной СЛАУ?

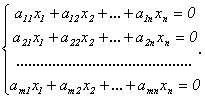
116. Перечислить свойства решений неоднородной СЛАУ.

Свойство 1. Сумма любого решения системы и любого решения соответствующей однородной системы является решением системы

Свойство 2. Разность любых двух решений неоднородной системы является решением соответствующей однородной системы

117. Какова структура общего решения неоднородной СЛАУ.

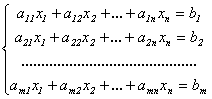
118. Сформулировать определение вектора.

Вектором называется направленный отрезок.

119. Сформулировать определение коллинеарных векторов.

Векторы называются коллинеарными. Если они лежат на одной прямой или на параллельных прямых.

120. Сформулировать определение равных векторов.

Равные, если она коллинеарна, имеют одинаковую длину и одинаковое направление.

121. Сформулировать правило сложения векторов.

Для сложения двух векторов  и  по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

122. Перечислить свойства сложения векторов.

• a + b = b + a.

• (a + b) + c = a + (b + c)

• Существует нулевой вектор такой, что а + 0 = а, для любого вектора.

• Для каждого вектора а существует противоположный ему вектор а’ такой, что а + а’ = 0.

123. Сформулировать определение разности векторов.

Разностью a – b вектора a – b называется такой вектор с, который в сумме с вектором b дает вектор а.

124. Сформулировать определение умножения вектора на число.

Произведением ненулевого вектора a на отличное от нуля число x называется такой вектор xa, для которого выполняются два условия: |x·a| = |x|·|a|; он сонаправлен с вектором a, если x > 0, и он направлен противоположно вектору a, если x < 0.

125. Перечислить свойства умножения вектора на число.

• k (a + b) = ka + kb

• (k + m) a = ka + ma

• k (ma) = (km) a

126. Сформулировать определение линейных комбинации векторов.

Линейной комбинацией векторов а₁, а₂…а_а называется выражение вида: к₁а1 + к₂а₂ +…+ k_na_n где k₁ – некоторые числа.

127. Сформулировать определение линейно зависимой системы векторов.

Система векторов A₁, A₂,...,A_n называется линейно зависимой, если существует ненулевой набор чисел λ_1,λ₂,...,λ_n, при котором линейная комбинация векторов λ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет ненулевое решение.

128. Сформулировать определение линейно независимой системы векторов.

Система векторов A₁, A₂,...,A_n называется линейно независимой, если линейная комбинация этих векторовλ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору только при нулевом наборе чисел λ_1, λ₂,...,λ_n, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет единственное нулевое решение.

129. Перечислить свойства линейно зависимых систем векторов.

Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

.

2. Если в системе векторов есть два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора  , то она линейно зависима.

4. Система из   векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

130. Сформулировать определение компланарных векторов.

Компланарны, если они лежат либо в одной плоскости, либо в параллельных плоскостях.

131. Сформулировать определение базиса.

Совокупность линейно независимых векторов n-мерного пространства называется базисом

132. Сформулировать определение координат вектора в базисе.

Числа   называются координатами вектора 

133. Перечислить свойства базиса.

равные векторы имеют одинаковые координаты,

   при умножении вектора на число его компоненты тоже умножаются на это число,

при сложении векторов складываются их соответствующие компоненты.

134. Сформулировать определение проекции вектора на ось.

Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора

135. Перечислить свойства проекции.

1. Проекции вектора на параллельные прямые (или на параллельные плоскости) равны.

2. Проекции равных векторов равны.

3. Проекция суммы векторов равна сумме их проекций.

4. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора,

5. Проекция линейной комбинации векторов равна линейной комбинации проекций.

136. Сформулировать определение декартовых координат вектора.

система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты

137. Сформулировать определение направляющих косинусов вектора

Косинусы углов, образованных вектором с осями координат, называются направляющими косинусами вектора

138. Перечислить свойства направляющих косинусов.

Направляющие косинусы пропорциональны соответствующим координатам:

139. Сформулировать определение скалярного произведения векторов.

Скалярное произведение двух векторов называется произведение их длин на cos угла между ними a*b = [a] * [b] * cosф

140. Перечислить свойства скалярного произведения.

Свойства скалярного произведения

• Свойство перестановки: a · b = b · a (от перестановки множителей скалярное произведение не меняется);

• Свойство распределения: a · (b · c) = (a · b) · c (результат не зависит от порядка умножения);

• Свойство сочетания (по отношению кскалярному множителю): (λ a) · b = λ (a · b).

• Свойство квадрата: a · a = a² = |a|² (скалярное произведения вектора самого с собой равняется квадрату его модуля);

• Если координаты векторов a={x₁, y₁, z₁} и b={x₂, y₂, z₂}, то скалярное произведение равно a · b = x₁x₂ + y₁y₂ + z₁z₂.

141. Сформулировать определение правой (левой) тройки векторов.

Тройка называется правой, если наблюдателю из их общего начала обход концов векторов a, b, c в указанном порядке кажется совершающимся по часовой стрелке. B противном случае a, b, c - левая тройка.

142. Сформулировать определение векторного произведения векторов.

Вектор с называется векторным произведением векторов a и b если, [c] = [a] * [b] * cosф, если c | a c | b.

143. Перечислить свойства векторного произведения.

1). 

2).  , т.е. векторное произведение антикоммутативно.

3).  , т.е. векторное произведение обладает распределительным свойством.

4). 

144. Сформулировать определение орта вектора.

Существуют так называемые орты - это единичные векторы, которые по направлению совпадают с осями координат. i - орт оси x, j - орт оси y, k - орт оси z.

145. Как находятся координаты произведения?

146. Сформулировать определение смешанного произведения векторов.

Смешанным произведением векторов abc называется результат скалярного умножения векторного произведения [ab] на вектор с.

147. Перечислить свойства смешанного произведения векторов.

1)Смешанное произведение равно нулю, если:

                        а) хоть один из векторов равен нулю;

                        б) два из векторов коллинеарны;

                        в) векторы компланарны.

            2)

           

148. Как находится смешанное произведение векторов с известными координатами.

149. Как выглядит уравнение прямой, проходящей через данную точку перпендикулярно данному вектору?

 А(х – х₀) + В(у – у₀) = 0 -                                                          (7.3)

уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

150. Сформулировать определение нормали прямой.

прямая, проходящая через эту точку и перпендикулярная к касательной прямой

151. Как выглядит общее уравнение прямой?

Ах + Ву + С = 0.  

152. Как выглядит каноническое уравнение прямой?

153. Сформулировать определение направляющего вектора прямой.

Направляющий вектор прямой — это любой ненулевой вектор, коллинеарный ей

154. Как выглядит уравнение прямой, проходящей через две заданные точки?

155. Как выглядит параметрические уравнения прямой?

 x = x₀ + lt,  y = y₀ + mt - параметрические уравнения прямой.

156. Сформулировать определение углового коэффициента прямой.

Угловой коэффициент прямой — коэффициент k в уравнении y = kx + b прямой на координатной плоскости, численно равен тангенсу угла между положительным направлением оси абсцисс и данной прямой линией.

157. Как выглядит уравнение прямой с угловым коэффициентом?

 у = kx + b 

158. Перечислить различные виды неполных уравнений прямой. Как располагается прямая относительно системы координат в каждом из перечисленных случаев.

1)       С = 0  - прямая Ах + Ву = 0 проходит через начало координат.

2)       В = 0  - прямая Ах + С = 0 параллельна оси Оу (так как нормаль к прямой {A,0} перпендикулярна оси Оу).

3)       А = 0  - прямая Ву + С = 0 параллельна оси Ох.

4)       В=С=0 – уравнение Ах = 0 определяет ось Оу.

5)       А=С=0 – уравнение Ву = 0 определяет ось Ох.

 

159. Как выглядит уравнение прямой в отрезках?

160. Как находится угол между прямыми?

 Если прямые L₁ и L₂ заданы общими уравнениями

А₁х + В₁у + С₁ = 0   и  А₂х + В₂у + С₂ = 0,

то угол между ними равен углу между их нормалями, то есть между векторами {A₁,B₁} и {A₂,B₂}.

161. Сформулировать условия параллельности двух прямых.

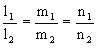
162. Сформулировать условия перпендикулярности двух прямых.

l₁ l₂ + m₁ m₂ + n₁ n₂ = 0

163. Как находится расстояние от точки до прямой?

Длина перпендикуляра, опущенного из данной точки на прямую

164. Как выглядит нормальное уравнение прямой?

165. Сформулировать определение отклонения прямой.

 Если d – расстояние от точки А до прямой L, то отклонение δ точки А от прямой L есть число +d, если точка А и начало координат лежат по разные стороны от прямой L, и число –d, если они лежат по одну сторону от L

166. Сформулировать теорему об отклонении прямой.

Теорема 7.1. Отклонение точки А(х₀,у₀) от прямой L, заданной уравнением (7.20), определяется по формуле:

            

167. Как выглядит уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору?

 A(x - x₀) + B(y - y₀) + C(z - z₀) = 0.  

168. Как выглядит общее уравнение плоскости?

169. Как выглядит неполные уравнение плоскости? Как в каждом из этих случаев располагается плоскость относительно системы координат?

Неполные уравнения плоскости.

   Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение (8.2) называют неполным.

Рассмотрим возможные виды неполных уравнений:

1)       D = 0 – плоскость Ax + By + Cz = 0 проходит через начало координат.

2)       А = 0 – плоскость By + Cz + D = 0 параллельна оси Ох.

3)       В = 0 – плоскость Ax + Cz +D = 0 параллельна оси Оу.

4)       С = 0 – плоскость Ax + By + D = 0 параллельна оси Оz.

5)       А = В = 0 – плоскость Cz + D = 0 параллельна координатной плоскости Оху 

6)       А = С = 0 – плоскость Ву + D = 0 параллельна координатной плоскости Охz.

7)       B = C = 0 – плоскость Ax + D = 0 параллельна координатной плоскости Оуz.

8)       А = D = 0 – плоскость By + Cz = 0 проходит через ось Ох.

9)       B = D = 0 – плоскость Ах + Сz = 0 проходит через ось Оу.

10)    C = D = 0 -  плоскость Ax + By = 0 проходит через ось Oz.

11)    A = B = D = 0 – уравнение Сz = 0 задает координатную плоскость Оху.

12)    A = C = D = 0 – получаем Ву = 0 – уравнение координатной плоскости Охz.

13)    B = C = D = 0 – плоскость Ах = 0 является координатной плоскостью Оуz.

170. Как выглядит уравнение плоскости в отрезках?

171. Как находится угол между плоскостями?

Если две плоскости (α₁ и α₂) заданы общими уравнениями вида:

  A₁x+B₁y+C₁z+D₁=0   и   A₂x+B₂y+C₂z+D₂=0,

то очевидно, что угол между ними равен углу между их нормалями, то есть между векторами n₁={A₁,B₁,C₁) и n₂={A₂,B₂,C₂)

172. Сформулировать условие параллельности плоскостей.

173. Сформулировать условие перпендикулярности плоскостей?

A₁A₂ + B₁B₂ + C₁C₂ = 0

174. Как выглядит уравнение плоскости, проходящей через три данные точки?

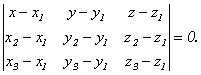
175. Как выглядит нормальное уравнение плоскости?

176. Как находится расстояние от точки до плоскости?

177. Сформулировать определение направляющего вектора прямой.

Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором

178. Как выглядит канонические уравнения прямой?

179. Как выглядит уравнение прямой, проходящей через две данные точки?

180. Как выглядит параметрические уравнения прямой?

181. Как найти угол между прямыми?

Угол между прямыми в пространстве равен углу между их направляющими векторами.  182. Как выглядит условие параллельности прямых?

183. Как выглядит условие перпендикулярности прямых?

184. Как найти угол между прямой и плоскостью?

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией на плоскость.

185. Как выглядит условие параллельности прямой и плоскости?

186. Как выглядит условие перпендикулярности прямой и плоскости?

Al + Bm + Cn = 0,   

187. Сформулировать определение линейного пространства.

ЛИНЕЙНОЕ ПРОСТРАНСТВО то  же, что векторное пространство

188. Сформулировать определение базиса линейного пространства.

 Базисом линейного пространства  называется конечная упорядоченная линейно независимая система векторов, что любой вектор пространства является линейной комбинацией этих векторов. 189. Что называется размерностью линейного пространства?

Число   называется размерностью пространства и обозначается 

190. Что называется координатами вектора в базисе?

Числа   называют координатами вектора   в базисе   и обозначают 

191. Какое пространство называется n – мерным?

Векторное пространство называется n-мерным, если в нем имеется n линейно независимых векторов, а всякие n+1 векторы линейно зависимы.

192. Сформулировать определение матрицы перехода от базиса к базису.

Матрицей перехода от базиса   к базису   является матрица, столбцы которой — координаты разложения векторов   в базисе  .

193. Записать формулу связи координат одного и того же вектора в разных базисах.

194. Сформулировать определение линейного оператора.

Пусть даны векторные пространства F и G. Функция А, сопоставляю-

щая каждому вектору из F определённый вектор из G, называется линейным

оператором

195. Сформулировать определение матрицы линейного оператора.

Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

196. Как связаны матрицы линейного оператора при переходе к новому базису?

197. Как связаны координаты образа и прообраза вектора при действии линейного оператора?

198. Сформулировать определение собственного вектора матрицы.

Собственным вектором матрицы А называется такой вектор, для которого справедливо соотношение

A·b = λ·b

199. Сформулировать определение собственных чисел матрицы.

Собственными числами матрицы   являются корни уравнения

и только они.

200. Сформулировать определение характеристического уравнения.

Характеристическое уравнение матрицы - алгебраическое уравнение вида

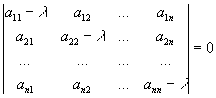
201. Сформулировать определение характеристического многочлена.

Характеристический многочлен — это многочлен, определяющий собственные значения матрицы.

202. Сформулировать алгоритм нахождения собственных чисел и собственных значений матрицы линейного оператора.

203. Сформулировать определение квадратичной формы.

Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.

204. Сформулировать определение симметрической матрицы.

Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали.

205. Перечислить свойства собственных чисел и собственных векторов симметрической матрицы.

1. Любая линейная комбинация собственных векторов   оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.

2. Собственные векторы   оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.

3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.