21''’. D-разбиение по 2 параметрам

Исследуем устойчивость систему по пар-ам К₁ и К₂. Тогда D(jω)=Re(K₁, K₂,ω)+jIm(K₁, K₂, ω)=0

{ ^{Re(K1, K2, ω)=0} _{Im(K1, K2, ω)=0}, (1) {^K1=f1(ω) _K2=f2(ω), (2) Изменяя ω от –  до + определяем границы устойчивости на плоскости К₁ К₂. Например:

Далее проводим штриховку. Правило штриховки:

1)вычисляется определитель:

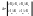
2) штриховка наносится слева, если при возрастании частоты w >0 и справа, если <0. 3) Далее строятся особые

прямые, связанные с переходом корня через мнимую ось в нач. координат (а₀=0) и через + (а_n=0) a_npⁿ+ a_n-1p^n-1+…+a₀=0 . На особые линии штриховка наносится в сторону двойной штриховки. Методика D-разбиения по двум параметрам: 1) выявление параметров по которым выполняется исследование 2) составление хар-го ур-ния, подстановка p=jω 3) формирование системы ур-ний (1) 4) решение сист. ур-ний, нахождение зависимостей (2) 5) построение областей устойчивости с учётом особенных линий 6) нанесение штриховки 7) проверка на устойчивость в одной т. области, претендующей на устойчивость Пример: D(p)=T₁T₂p³+ (T1+T2) p² +p+k=0, -j T₁T₂ω³- (T1+T2)p²+jω+k=0,

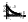{ ^{Re(k,T1, ω)=k-(T­1+T2) ω2=0} _{Im(k,T1, ω)= ω-T1T2ω3=0}, Из (2) урав.: T₁=1/T₂ω². Из (1) урав.: k=(1/T₂)+T₂ω²

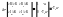
ω изм-ся (-,0)  >0; ω изм-ся (0,-)  <0

Особые линии: a₀=0  K=0; a_n=0  T₁T₂=0 T₁=0

2 2. Установившиеся режимы в сау и точность в установившемся режиме.

I все звенья статические W(p)=(b_mp^m+…+b₀)/ (a_npⁿ+…+a₀);В установившемся режиме:t p0 W(0)=b₀/a₀=k1) если система разомкнута: Y(p)=W_y(p)U_з+W_of*f; При переходе к установившемуся значению t p0 : Y_уст=k_yk_oyU_з

+k_of*f ; k_yk_oy=k_p; Y_y^уст=k_pU_з , U_з=y_y^уст/k_p Y_f^уст=

k_of*f , y_уст=k_of*f Статическое отклонение: =

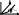 y/y_зд= k_of*f/ y_зад 2) Замкнутая система:W_зу(p)= W_у(p)*W_oy(p)/1+W_у(p)*W_oy(p)*W_д(p), W_зe(p)=1/ 1+ W_у(p)*W_oy(p)*W_д(p), W_зf(p)=W_of(p)/1+W_у(p)* W_oy(p) W_д(p), Y_уст=k_yk_oyU_з/(1+k_yk_oyk_д) при р0 , U_з=Y_зад* k_д, E_уст=1*U_з=/1+k_yk_oyk_д, K_у≥ (1/k_yk_oy) * ((U_з/E_з)-1), y_уст=W_зf(0)*f= k_of*f/1+k_yk_oyk_д= k_of*f/1+k_p, _з=y/y_з=k_of*f/((1+k_p)*y_з)=_p/1+k_p, k_y≥ (1/k_yk_oy)*((k_of*f/ y_зд*_з)-1). II. Астатическая система- это система в разомкнутом виде т.е есть интегратор не охваченной местной обратной связью. W_p(p)=M(p)/pυ*D(p), где υ - порядок астатизма,W_y(p)=k_и/p=1/T_иp, k_и[1/c], U(t)=k_и∫E(t)dt, Y(p)=W_зу(p)*U_з=(k_и*W_оу(p)/p)/(1+(k_и*W_оу(p)* W_д(p)) /p)=(( k_и*W_оу(p))/(p+k_и*W_оу(p)*W_д(p)))*U_з; y_уст= (k_yk_oy/k_дk_yk_oy)*U_з=U_з/k_д при p0, E(p)= 1*U_з/(1+(k_и/p)* W_оу*W_д)=(p/p+W_оу*W_д*k_и)*U_з, E_уст=(0/k_иk_oyk_д)*U_з=0, U_з=U₀t=∫U₀dt, E_уст=U₀/ k_иk_oyk_д

y(p)=W_зf(p)*f(p)=W_of(p)/(1+k_и/p* W_оу*W_д)=p*W_оf(p)/(p+k_и*W_оу*W_д). Y_уст 0,р0. Для линейно возрастающего сигнально управл. или

возмущения, будет существ. ошибка слежения по скорости. От нее можно избавиться если ввести еще один интегратор. Но введение интегратора не яв-ся безобидной операц. т.к увелич. колебан. приближ. к границе устойчив. в плоть до полной потери устойчивости.