19. Применение критерия Найквиста при наличии астатических и консервативных звеньев.

А статическое звено:W(p)=K_и/p, можно представить как предельный случай 1-го порядка т.е = lim_α→0K_и/(p+α)= (K_и/α)/(1/2*p+1)=K/T_p+1, α→0, K= K_и/α→∞. T=1/α. Тогда можно считать что АФХ

а статического звена начин. на вещественной полуоси в бесконеч. и по дуге бесконеч. радиуса замык. на мнимой оси. т .е рис№2. Видно что АФХ не охватывает т. (-1;j0). Замкнутая САУ будет устойчивой. Пусть разом. система содержит 2 интегратора. W_p(p)=(K_и1/p)+(K_и2/p) => W_p(jω)=(K_и1*K_и2)/jω=- K_и1*K_и2/ω². Видим(рис№3) что при любых знач. параметра K_и1 и K_и2 замкнутая САУ будет наход. на гран. уст-ти. Услов. нахожден. системы на гр. устойчивости W(jω)=-1 можно разбить {^P(ω)=-1_Q(ω)=0,

- K_и1*K_и2/ω²=-1, ω= K_и1*K_и2 . Рассмотрим 3 интегратора:

W _p(p)=K₁*K₂*K₃*K_д/p³

АФХ раз. системы охват. т(-1;j0), замкн. САУ будет не устойчива при любых знач. параметров K₁,K₂,K₃, K_д. Системы которые

б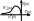 удут не устойчивы при любых знач-ях параметров элементов назыв. структ. неусточивыми.

Систему можно устойчивой если преобразовать ее. Например охватив интегратор линейной обратной связью W_э(p)=(K_и/p)/(1+(K_и*K_α/p))=

K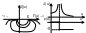 _и/(р+K_и*K_α)=(1/K_α)/((1/K_иK_α*р)+1). Консервативно колебательное звено: W(p)=K/T²p²+1= lim_ρ→0K/T²p²+2ρTp+1.

W _p(p)=K/(T₁p+1)³(T₂² p²+1), T₁>T₂.

W_p(p)=K/(T₁p+1)(T₂² p²+1).

20. Влияние запаздывания на устойчивость сау.

П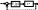 усть имеем или можем выделить в системе звено чистого запаздывания

Проанализируем влияние запаздывания

н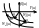 а устойчивость системы после замыкания обратной связи. Используя критерий Найквиста W_p(p)= W₁(p)e^-p. КЧХ(АФХ) W_p(jw)=A₁(w)*e^j1(w)* e^jw= A₁(w) * e^{j[1(w)-w]}. Видим, что чистое запаздывание не влияет на модуль АФХ, но увеличивает сдвиг по фазе выходного сигнала. АФХ разомкнутой системы можно построить по АФХ W₁(jw), где каждый радиус-вектор W₁(jw) для частоты w_i следует дополнительно повернуть по часовой стрелке на угол w_i.

П ри некотором значении запаздывания  система может оказаться на границе устойчивости. (рис№2). Условие попадания на границу устойчивости имеет вид:

{^A1(wкр)=1_{1(wкр)- wкр* tкр= -}, w_кр* t_кр=+1(w_кр), t_кр= (p+j1(w_кр)) /w_кр, При всех значениях t<t_кр замкнутая система будет устойчива,

а при t>t_кр- неустойчива.