
- •Предел функции в точке. Единственность предела. Ограниченность функции, имеющей предел.
- •2Бесконечно малые функции.Теорема о связи функции её предела и бесконечно малой.Свойства бмф.
- •Необходимость. Из дифференцируемости функции выводим существование производной.
- •Билет 21Первообразная функция.
- •Билет 22Способ подстановки (замены переменных неопред интеграл).
- •Билет 23 Определенный интеграл.
- •Свойства определенного интеграла.
- •25 Билет Интегрирование по частям .Определённый интеграл
Билет 23 Определенный интеграл.
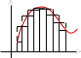
Пусть на отрезке [a, b] задана непрерывная функция f(x).
 y
y
M
m
0 a xi b x
Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a, b]
Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.
x0 < x1 < x2 < … < xn
Тогда x1 – x0 = Dx1, x2 – x1 = Dx2, … ,xn – xn-1 = Dxn;
На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции.
[x0, x1] ® m1, M1; [x1, x2] ® m2, M2; … [xn-1, xn] ® mn, Mn.
Составим суммы:
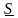 n
= m1Dx1
+ m2Dx2
+ … +mnDxn
=
n
= m1Dx1
+ m2Dx2
+ … +mnDxn
=

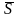 n
= M1Dx1
+ M2Dx2
+ … + MnDxn
=
n
= M1Dx1
+ M2Dx2
+ … + MnDxn
=
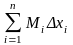
Сумма называется нижней интегральной суммой, а сумма – верхней интегральной суммой.
Т.к. mi £ Mi, то n £ n, а m(b – a) £ n £ n £ M(b – a)
Внутри каждого отрезка выберем некоторую точку e.
x0 < e1 < x1, x1 < e < x2, … , xn-1 < e < xn.
Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].
Sn
= f(e1)Dx1
+ f(e2)Dx2
+ … + f(en)Dxn
=
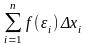
Тогда можно записать: miDxi £ f(ei)Dxi £ MiDxi
Следовательно,
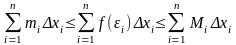

Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной. Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Свойства определенного интеграла.
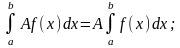
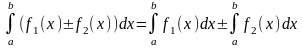
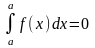
Если f(x) £ j(x) на отрезке [a, b] a < b, то
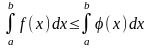
Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что
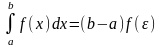
Доказательство: В соответствии со свойством 5:
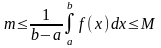
т.к. функция f(x) непрерывна на отрезке [a, b], то она принимает на этом отрезке все значения от m до М. Другими словами, существует такое число eÎ [a, b], что если
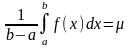 и m
= f(e),
а a
£
e
£
b,
тогда
.
Теорема доказана.
и m
= f(e),
а a
£
e
£
b,
тогда
.
Теорема доказана.
7) Для произвольных чисел a, b, c справедливо равенство:
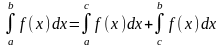
Разумеется, это равенство выполняется, если существует каждый из входящих в него интегралов.
8)
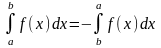
Обобщенная теорема о среднем. Если функции f(x) и j(x) непрерывны на отрезке [a, b], и функция j(х) знакопостоянна на нем, то на этом отрезке существует точка e, такая, что

Билет 24Производная определённого интеграла
Формула Ньютона – Лейбница
Пусть
в интеграле
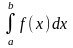 нижний предел
нижний предел
а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
Обозначим
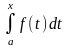 = Ф(х). Найдем производную функции Ф(х)
по переменному верхнему пределу х.
= Ф(х). Найдем производную функции Ф(х)
по переменному верхнему пределу х.

Аналогичную теорему можно доказать для случая переменного нижнего предела.
Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
Теорема: (Теорема Ньютона – Лейбница)
Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то
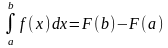
это выражение известно под названием формулы Ньютона – Лейбница.
Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция - первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то

при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:

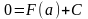

Тогда
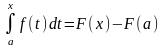 .
.
А
при х = b:

Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:
Билет 25 Замена переменной в определённом интеграле:
Теор: пусть 1) Функция ¦(t) непрерывна на [a,b]. 2) Отрезок [a,b] явл. множеством значений функции t=g(x), xÎ[a,b], причём g'(x) непрерывна на [a,b]. 3) g(a)=a; g(b)=b. Тогда òab¦(t)dt=òab¦(g(x))g'(x)dx [1] -формула замены переменной под знаком определенного интеграла. Док: пусть F(t) - некоторая первообразная функции ¦(t) на отрезке [a,b] (она существует в силу непрерывности ¦(t)). Тогда òab¦(t)dt=F(b)–F(a) [2]. Функция F(t) дифференцируема на [a,b], поэтому дифференцируема и функция F(g(x)), отрезке [a,b], причем dF(g(x))/dx=F'(g(x))g'(x)= ¦(g(x))g'(x). Стало быть по формуле Ньютона-Лейбница, òab¦(g(x))g'(x)=F(g(b))–F(g(a))= F(b)–F(a) [3]
Сравнивая формулы [2] и [3], получаем [1]. Теор. док.
Вычисление определённого интеграла по частям:
Теор: Пусть функции u(x) и v(x) имеют непрерывные производные на отрезке [a,b]. Тогда справедлива формула òabu(x)v'(x)dx=u(x)v(x)|ab–òabv(x)u'(x)dx [1]. - формула интегрирования по частям для определенного интеграла и записывают её еще в виде òabudv=uv|ab–òabvdu. Док: заметим, что функция u(x) и v(x) явл. первообразной для функции (uv)'=u'v+uv', причем
эта функция непрерывна. => òab(u'(x)v(x)+u(x)v'(x))dx= (u(x)v(x))|ab [2]. Т.к. u'(x)v(x), u(x)v'(x) - непрерывные на [a,b] функции, то определённые интегралы от этих функций сущ. и формулу [2] можно записать в форме [1]. Теор. док.
