
- •Предел функции в точке. Единственность предела. Ограниченность функции, имеющей предел.
- •2Бесконечно малые функции.Теорема о связи функции её предела и бесконечно малой.Свойства бмф.
- •Необходимость. Из дифференцируемости функции выводим существование производной.
- •Билет 21Первообразная функция.
- •Билет 22Способ подстановки (замены переменных неопред интеграл).
- •Билет 23 Определенный интеграл.
- •Свойства определенного интеграла.
- •25 Билет Интегрирование по частям .Определённый интеграл
Необходимость. Из дифференцируемости функции выводим существование производной.
Дифференциалом функции называют главную часть приращения в точке х, соответствующим приращению аргумента Dх. Дифференциал dy=ADx=f’(x)Dx или dy=f’(x)dx.
Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x0,f(x0)) при изменении x0 на величину Dx
Св-ва: 1(U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx, d(U±V)=d(U±V)
2.
(UV)`=U`V+V`U, то
(UV)`dx=V`dU+U`dV 
3.d(c)=c`dx=0*dx=0
4. d(U/V)`=(V`dU-U`dV)/V2.
БИЛЕТ 9непрерывность дифференцируемой функции
Теорема.
Если функция
f(x)
дифференцируема в точке х,
то f(x)
непрерывна в точке x.
Доказательство.
Пусть функция
f(x)
дифференцируема в точке
x,
т.е. Dy=ADx+o(x)
(Dx®0).
Тогда
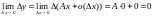 ,
т.е. функция f(x)
непрерывна в точке x.
Производная
суммы
(разности) двух
дифференцируемых функций равна сумме
(разности) производных этих функций:
,
т.е. функция f(x)
непрерывна в точке x.
Производная
суммы
(разности) двух
дифференцируемых функций равна сумме
(разности) производных этих функций:
(U±V)`=U`±V`,Производная произведения функций.
Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и (UV)`=U`V+V`U
Производная частного функций.
Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле. d(U/V)`=(V`dU-U`dV)/V2.
Производная сложной функции
Если
функция u=φ(x)
имеет производную
 в
точке х,а функция y=f(u)
имеет производную .
в
точке х,а функция y=f(u)
имеет производную .
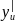 в соответствующей точке u=
φ(x),то
сложная функция y=f(φ(x))
имеет производную
в соответствующей точке u=
φ(x),то
сложная функция y=f(φ(x))
имеет производную
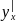 в точке х,которая находится по формуле
в точке х,которая находится по формуле
= *
Для нахождения нужно производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независемому аргументу
Билет 10 производная обратной функции
Производная
обратной функции равна обратной величине
производной данной функции
=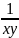
Основные
формулы:

Для сложных функций:
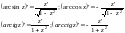
Билет 11Пусть функция y = f ( x ) дифференцируема на некотором отрезке [ a , b ]. Значения производной f'(x) зависят от х, т.е. производная f'(x) тоже представляет собой некоторую функцию от х. Дифференцируя эту функцию, мы получаем производную от производной.
О. Производная от первой производной называется производной второго порядка или второй производной. Обозначается
y''=( f'( x ))'= f''( x ). (4.5)
Физический смысл второй производной: вторая производная f''(x) равна скорости изменения скорости, т.е. ускорению движущейся точки в момент времени х.
Вторая производная также может быть функцией, определенной на некотором множестве. Если эта функция имеет производную, то эта производная называется третьей производной функции f(x) и обозначается f'''(x).
О. Если определена ( n -1) -я производная f (n -1 ) (x) и существует её производная, то она называется n-й производной функции f(x):
f ( n ) ( x ) = ( f ( n -1 ) ( x ))' . (4.6)
Все производные, начиная со второй, называются производными высших порядков.
Функцию, имеющую на данном множестве конечную производную порядка n , называют n раз дифференцируемой на данном множестве.
Дифференциал функции y = f ( x ) выражается в виде dy = f'( x ) dx . Тогда, если он является некоторой функцией от х, то справедливо следующее:
О. Дифференциал от дифференциала функции называется дифференциалом второго порядка или вторым дифференциалом:
d 2 y = f''( x ) dx 2 . (4.7)
О. Дифференциал от дифференциала n -го порядка называется дифференциалом ( n +1)-го порядка.
Билет 19Направление выпуклости. Точки перегиба. Необходимое и достаточное условия. Исследование по высшей производной.
Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках. Линия называется вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.
Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.
Необходимый признак выпуклости и вогнутости: если линия на интервале выпуклая, то ее 2я производная <=0; если линия на интервале вогнутая, то ее f``(x)>=0
Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; если f``(x)>0, то линия вогнутая.
Признаки точки перегиба: чтобы X0 была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через
Билет 20Исследование функции на экстремум с помощью производных высших порядков
Пусть в точке х = х1 f¢(x1) = 0 и f¢¢(x1) существует и непрерывна в некоторой окрестности точки х1.
Теорема. Если f¢(x1) = 0, то функция f(x) в точке х = х1 имеет максимум, если f¢¢(x1)<0 и минимум, если f¢¢(x1)>0.
Доказательство.
Пусть f¢(x1) = 0 и f¢¢(x1)<0. Т.к. функция f(x) непрерывна, то f¢¢(x1) будет отрицательной и в некоторой малой окрестности точки х1.
Т.к. f¢¢(x) = (f¢(x))¢ < 0, то f¢(x) убывает на отрезке, содержащем точку х1, но f¢(x1)=0, т.е. f¢(x) > 0 при х<x1 и f¢(x) < 0 при x>x1. Это и означает, что при переходе через точку х = х1 производная f¢(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум.
Для случая минимума функции теорема доказывается аналогично.
Сема построения графика
Найти область определения функции.
Найти область значений функции. Обычно этот пункт пропускают или заполняют после исследования на экстремумы.
Исследовать непрерывность функции, выделить особые точки (точки разрыва).
Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Найти точки пересечения с осями координат.
Найти нули функции. Найти интервалы знакопостоянства функции.
Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции.
Установить, является ли функция периодической или нет. Обычно проверяют для тригонометрических функций, для других данный пункт пропускается.
Найти первую производную. Найти точки экстремума (локального минимума и максимума) и интервалы монотонности (возрастания и убывания) функции.
Найти вторую производную. Найти точки перегиба и интервалы выпуклости-вогнутости.
Найти наклонные/горизонтальные асимптоты функции.
Исследовать поведение функции на бесконечности.
Построить график функции. Построить асимптоты.
Отметить важные точки на графике.
