9 Моделирование кривых и поверхностей в форме Безье

Представление кубических кривых в форме Безье.

Кубическая кривая в форме Безье описывается при помощи четырех точек ( P1, P2, P3, P4 ), при этом отрезки P1, P2 и P3, P4 определяют направление касательных векторов.

С математической точки зрения форма Эрмита и форма Безье описывает одну и ту же кривую. Поэтому между этими двумя формами описания сегментов можно ввести соотношение:

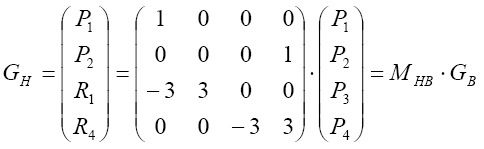
Используя выражение найдем уравнения для формы Безье:

где T - вектор степеней параметров, M_B - матрица Безье, а G_B – геометрическая матрица Безье, описывающая исходные данные:

При этом матрица Безье имеет следующий вид:

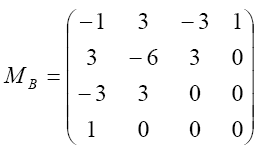
По сравнению с формой Эрмита форма Безье имеет следующие преимущества:

• сегмент кривой удобно задавать в интерактивном режиме по четырем точкам;

• четыре точки определяют четырехугольник, который может использоваться в качестве выпуклой оболочки в процедуре удаления невидимых линий и поверхностей.

Недостатком данной формы, по сравнению с формой Эрмита является то, что она не позволяет с математической точностью определить гладкость сопряжения сегментов.

Чаще всего в системах проектирования и конструирования, формы Безье и Эрмита используется совместно. При помощи формы Безье происходит интерактивный ввод кривых, а достижение требуемой гладкости обеспечивается переходом от формы Безье к форме Эрмита с последующей коррекцией величин касательных.

Формы Эрмита и Безье является наиболее простым представлением кубических кривых. Они обладают следующими общими недостатками:

• изменение координат хотя бы одной точки приводит к необходимости изменений всей кривой;

• добавление узла в кривую также приводит к необходимости пересчета всей кривой.

Модель поверхности формы Безье.

Для описания кривой линии в форме Безье было достаточно четырех точек в трехмерном пространстве. Для описания сегмента поверхности требуется 4*4=16 точек. При этом сегмент поверхности аппроксимируется многогранником, у которого только четыре угловые точки совпадают с точками самой аппроксимируемой поверхности. Остальные определяют охватывающий многогранник. Таким образом, матрица описания сегмента в форме Безье будет содержать координаты шестнадцати точек: .

Уравнение, определяющее один сегмент поверхности Безье, будет иметь бикубическую форму:

(1)

где параметры u є [0,1]; t є [0,1] , а функции

Данная кривая описывает бикубическую пространственную форму. Запишем ур-е (1) в матричном виде: r(u,t) = G_u*P*G_t

где P - матрица исходных данных, а векторы G_u и G_t имеют следующий вид:

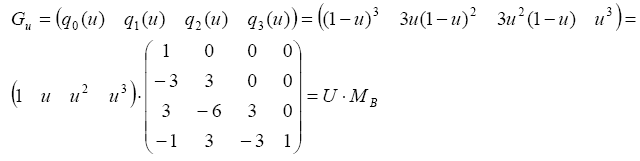
Аналогичным образом определяется последняя составляющая этого уравнения G_t :

Подставим выражения G_u и G_t, получим:

10 Моделирование кривых и поверхностей в форме Эрмита

Пусть P₁ и P₄ - концевые точки сегмента кривой, а R₁ и R₄ - касательные в них.

Н

Рис 1.

еобходимо найти коэффициент системы уравнений (1), исходя из условий (2):

x(t) = ax t3 + bx t2 + cx t + dx ; y(t) = ay t3 + by t2 + cy t + dy ; (1) z(t) = az t3 + bz t2 + cz t + dz ;

r(0) = P1 = (P1x P1y P1z ); r(1) = P4 = (P4x P4y P4z ); r′(0) = R1 = (R1x R1y R1z ); (2) r′(1) = R4 = ( R4x R4y R4z ).

Рассмотрим реш-е задачи на прим одного ур-я. Для компакт-ти представим ур-я в векторном виде:

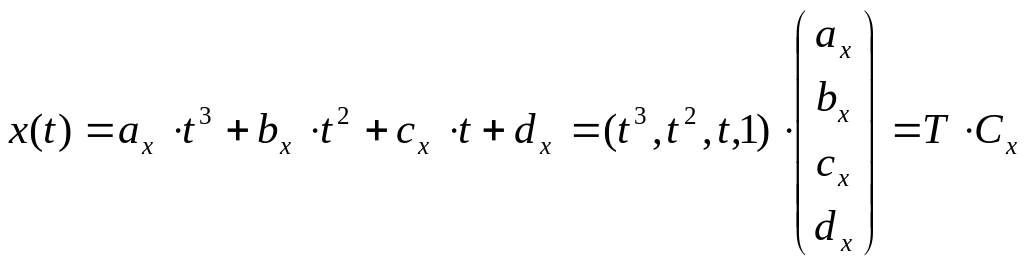(3)

где T - вектор-строка степеней параметра t, Cx - вектор-столбец коэф-тов для первого уравнения системы (1). Представим исходные данные в векторной форме:

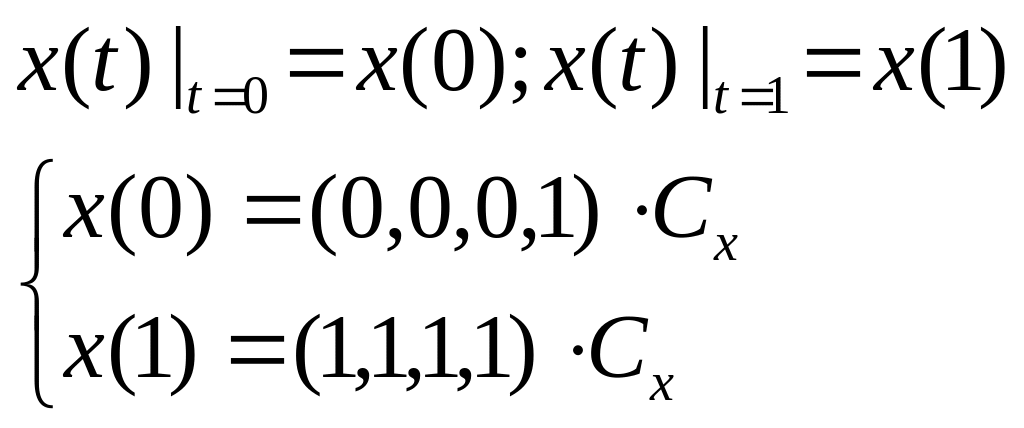(4)

Для получения значений производных продифференцируем выражение x(t):

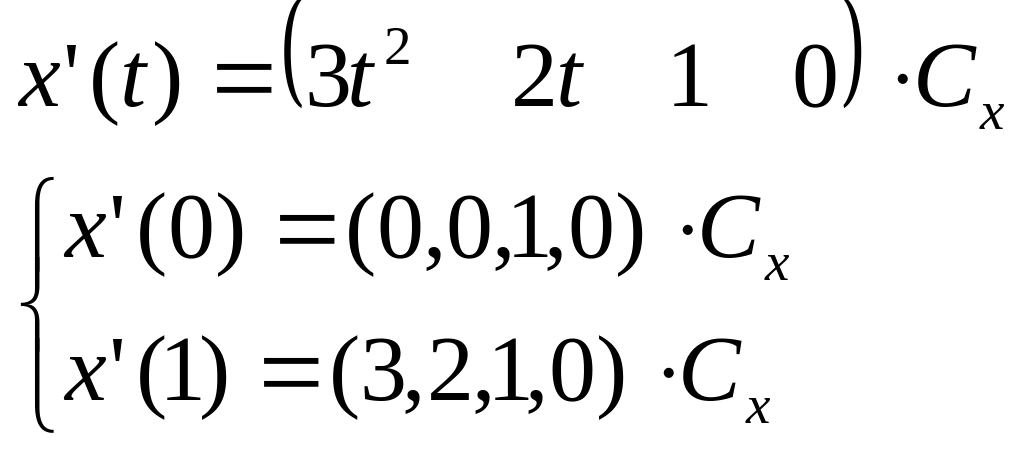(5)

Объединим отдельные векторные выражения формул (4) и (5) в единую систему уравнений, которые описываются одним матричным уравнением:

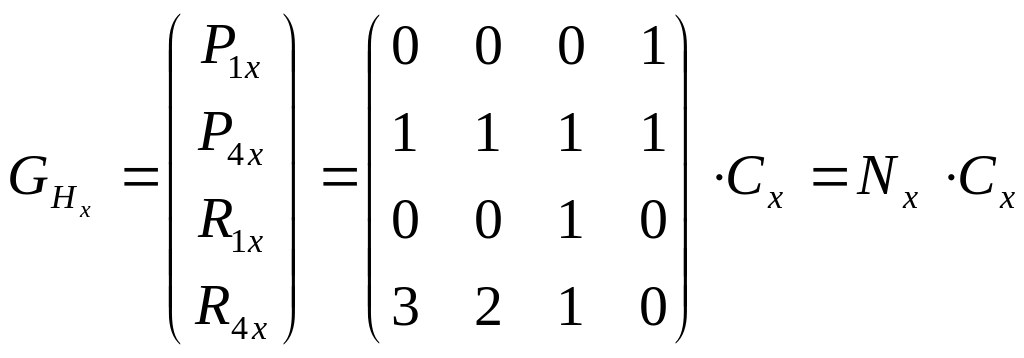(6)

где G_Hx - геометрическая матрица Эрмита, содержащая исходные данные для описания сегмента кривой линии. Решая выражение (6) относительно вектора Cx, получим следующий результат:

(7)

где – M_H = N^-1_H матрица сопряжения Эрмита, а G_H - вектор Эрмита.

Подставим (7) в (3), получим x(t) = T * M_H *G_Hx.

Аналогичным образом получим соответствующие уравнения для координат y и z, тогда 3 матричных уравнения можно записать в следующем виде:

r(t) = T * M_H *G_H.

Имея исходные данные, содержащиеся в G_H и изменяя значения параметра T от нуля до единицы можно восстановить с заданной точностью точки сегмента.

При построении гладких поверхностей необходимо следить за поведением кривой на каждом из сегментов. Ее поведение будет зависеть от величин касательных R1 и R4.

ПОВЕРХНОСТЬ ЭРМИТА

Д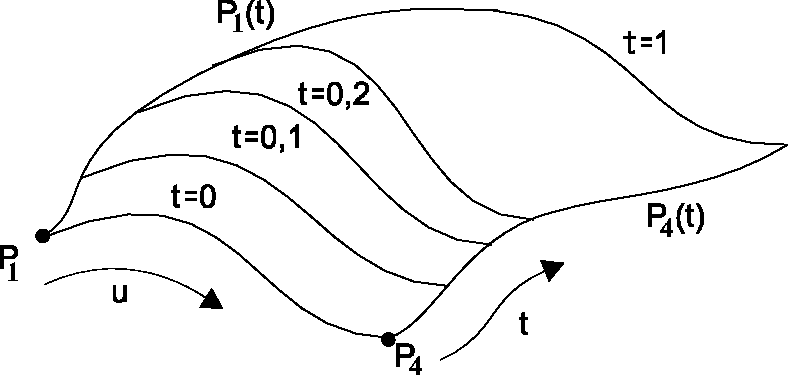 ля моделирования сегмента трехмерной поверхности в данной форме используются координаты концевых (угловых) точек сегмента и касательные векторы в них. На основании этих исходных данных определяется коэффициент бикубического многочлена – aij. Описание кривой линии в трехмерном пространстве, в форме Эрмита определяется:

Перемещая подобную кривую во времени получим:

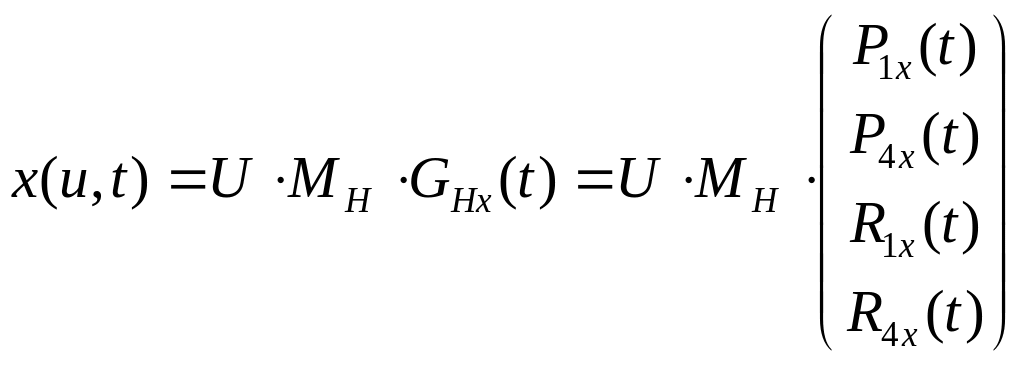(1)

Если интерполируемые линии являются прямыми, то полученная поверхность называется линейчатой. Если, кроме того, кривые P₁(t) и P₄(t) находятся в одной плоскости, то моделируемый сегмент будет плоским.

Представим четыре многочлена в виде одного вектора:

(3)

где .

Используя тождество матричной алгебры применительно к выражению (3), получим следующие значения:

(4)

где

П одставив (4) в (1), получим:

(5)

А налогичным образом получается выражение для зависимостей у(u,t) и z(u,t). Таким образом, задача конструирования поверхности в форме Эрмита заключается в определении элементов матриц