1 Аксонометрические проекции. Изометрия, диметрия, триметрия 2

2 Алгоритмы разложения в растр отрезка прямой линии и окружности 5

3 B-сплайновые модели кривых, поверхностей и их разновидности 7

4 Использование методов порталов и иерархических подсцен при создании виртуальной реальности. 9

5 Классификация цветовых моделей и форматов компьютерной графики 10

6 Колориметрия. Цветовые модели, смешение цветов и законы Гроссмана 13

7 Математическая модель и виды перспективного проецирования 15

8 Методы геометрического моделирования 17

9 Моделирование кривых и поверхностей в форме Безье 19

10 Моделирование кривых и поверхностей в форме Эрмита 21

11. Моделирование прозрачности и теней при построении реалистических изображений 23

12. Моделирование трехмерных поверхностей порциями поверхностей Кунса 25

13 Моделирование фотореалистичных изображений при помощи метода излучательности 27

14. Построение реалистических изображений методом Торренсанса-Сперроу 29

15. Построение реалистичных изображений. Формула закраски 31

16. Преобразования на плоскости и в пространстве. Система однородных координат 33

17. Развертка сплошных областей. Алгоритмы построчной развертки и заполнения с затравкой. 37

Построение В-сплайновой модели поверхности происходит на базе В-сплайновой модели кривых и полностью аналогично построению модели по форме Эрмита и Безье. Формат поверхности формы В-сплановой поверхности описывается следующим уравнениями: 41

41

19. Формирование изображений трехмерного пространства методом отсечения лучей. 42

20. Формирование изображений трехмерного пространства при помощи алгоритмов, основанных на построении BSP-деревьев 44

21. Формирование окраски методом Гуро 47

22. Формирование окраски методом Фонга 49

23. Формирование реалистических изображений методом трассировки лучей 50

24. ЦВЕТОВЫЕ МОДЕЛИ, ОРИЕНТИРОВАННЫЕ НА АППАРАТУРУ И ВОСПРИЯТИЕ ЧЕЛОВЕКОМ 52

25. Цветовые форматы и стандарты МКО 55

1 Аксонометрические проекции. Изометрия, диметрия, триметрия

Параллель проекция – аксонометр, если линии проецирования перпендик-ны плоск-ти проецир-я.

У параллель проекции центр проецир-я удален в бесконечность, и линии проециря-я параллельны.

При их построении используется аппарат аффинной геометрии. С формальной точки зрения аффинные преобразования определяются матрицей преобразований Т, в которой четвертый столбец имеет вид:

Среди аксонометрических проекций различают прямоугольную, диметрическую, изометрическую и триметрическую проекции.

Прямоугольные проекции

Ортографические проекции - частный случай ортогональных (прямоугольных) проекций, проецирование здесь - на координатные плоскости. Общий вид матрицы преобразований для получения прямоугольной (ортографической) проекции:

При этом два из трёх диаг-х элементов (а, е, i) равны единице, а третий должен быть нулевым.

В общем случае для выполнения ортогональных построений необходимо сместить плоскость проецирования параллельно одной из координатных плоскостей.

Ортогональное проецирование определяется матрицей преобразований с нулевой строкой, соответствующей той оси, перпендикулярно которой находится плоскость проецирования.

Ортогональные и ортографические проекции находят широкое применение в техническом черчении. Совокупность двух или трех ортографических проекций называется эпюром Монжа.

Диметрия и изометрия

Для построения более сложных аксонометрических проекций необходимо использовать комбинацию преобразований поворотов и проекций из бесконечности. Рассмотрим пример проецирования на плоскость Z = 0 .

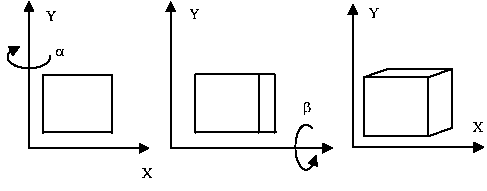
Для получения данн изобр-я необх воспользоваться пространственным преобразованием:

,

где (Ry - матрица поворота вокруг оси OY по часовой стрелке, Rx – матрица поворота вокруг оси OX против часовой стрелки (α<0, β>0)).

Диметрическая проекция

Для построения необх, чтобы масштаб по осям ОX и ОY были - 1:1, а по оси OZ - 1:2.

Рассмотрим единичные векторы e_X, e_Y и e_Z, расположенные в исходном трёхмерном пространстве. В системе однородных координат их величины будут выглядеть следующим образом:

После преобразований по уравнению получим:

При этом по определению диметрии имеем следующие соотношения:

Используя теорему Пифагора, последние равенства можно записать в виде:

Решая эту систему относительно α и β получим углы поворота β =-20.705°; α = 22.208°.

Подставим полученные значения тригонометрических функций в уравнение и получим значения элементов матрицы преобразований для построения диметрической проекции в плоскости XOY (Z = 0):

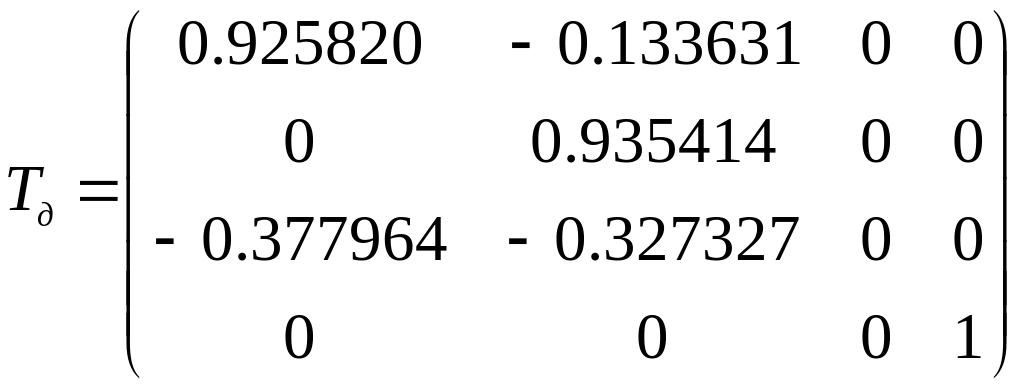
Угол, образуемый проекцией оси ОХ с горизонталью плоскости проецир-я будет опред-ся через tgφ:

Для оси OY:

Для оси OZ:

Изометрическая проекция

При построении изометрии масштаб по всем трём осям должен быть одинаковым, поэтому соотношение длин единичных векторов:

Аналогично, с использованием теоремы Пифагора, составим систему уравнений:

Решая эту систему относительно α и β получим углы поворота β =35.264°; α = 45°.

После подстановки значений тригонометрических функций вычисленных углов в уравнение получим матрицу преобразований для построения изометрии:

По аналогии с диметрией рассчитываются углы, которые составляют проекции осей координат с горизонталью плоскости проекции:

Последний вид аксонометрической проекции – триметрическая проекция - не ограничена каким-либо соотношением по координатным осям, поэтому для её построения в любом случае нужно производить самостоятельные расчёты углов поворота и матриц преобразований Т, аналогично тому, как это было сделано для диметрии и изометрии.