3.2.7 Звено чистого запаздывания

Динамическая его характеристика имеет вид: у=х*(t – τ), где τ – время чистого запаздывания. График переходного процесса:

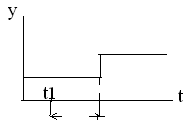
Характеристика – величина у на выходе звена = вх величине х, но через время τ. Передаточная функция имеет вид: W(р)=у(р)/х(р)=е^-р*τ

3.3 Передаточные функции аср

Отношение преобразованной по Лапласу выходной величины АСР (или элемента) к преобразованной по Лапласу входной величины АСР называется передаточной функцией АСР (элемента).

У(Р)/ Х(Р) =(b_0*P^m+ b_1*P^m-1+…+ b_m-1*P+b_m)/(a₀*Pⁿ+ a₁*P^n-1+…+ a_n-1*P+a_n) =W(P)

Знаменатель передаточной функции приравнивают к 0, и такая функция называется характеристическое уравнение АСР(или элемента).

Любая АСР состоит из отдельных звеньев, элементов, соединенных по следующим схемам:

1.последовательное соединение элементов

2. параллельное соединение

3. смешанное соединение элементов

4. соединение элементов по схеме обратной связи

Для определения передаточной функции данной АСР необходимо определить передаточные функции вышеуказанных элементов в схеме.

3.3.1 Последовательное соединение звеньев

W₁(P)

W₂(P)

W_n(P)

Х₃(Р) Х_n(P) Х_n+1(Р), У(Р)

Х ₁(Р) ……

Х(Р)

W₁(P)… W_n(P)-передаточная функция отдельных звеньев.

На входе и выходе – входные и выходные сигналы. Входные сигналы первого звена равны сигналу всей системы. Х₁(Р) = Х(Р)

Вся система обозначена как W(Р). Выходной сигнал всей системы У(Р):

Х_n+1(Р)=У(Р)

W(Р)= У(Р)/ Х(Р)

Определяющим выражением передаточной функции для каждого звена является отношение выходного сигнала к входному.

W₁(P) =X₂(P)/X₁(Р); W₂(P)=X₃(P)/X₂(Р)

W_n(P)=X_n+1(P)/X_n(Р)

Перемножим соотношения:

W₁(P)* W₂(P)* W_n(P)= X_n+1(P)/X₁(Р)= У(Р)/ Х(Р) =W(P)

Передаточная функция АСР, состоящая из n последовательно соединенных звеньев равна произведению передаточных функций звеньев.

3.3.2 Параллельное соединение звеньев

W₁(P)

У₁(Р)

Х₁(Р) W(Р)

W₂(P)

W_n(P)

Х 2(Р) У₂(Р) У(Р)

Х n(Р) У_n(Р)

Входной сигнал системы равен входному сигналу всех элементов. Х(Р) = Х₁(Р)= Х₃(Р)= Х_n(Р)

Выходные сигналы АСР равен сумме входных сигналов его элементов:

У₁(Р)= W₁(Р)* Х(Р)

У₂(Р)= W₂(Р)* Х(Р)

У_n(Р)= W_n(Р)* Х(Р)

У(Р)=У₁(Р)+ У₂(Р)+ У₃(Р)+ +У_n(Р) (3.1)

В формулу 3.1 подставим получен. ранее выходных сигналов каждого элемента У(Р)= W₁(Р)* Х(Р)+ W₂(Р)* Х(Р)+ ..+ W_n(Р)* Х(Р)

У(Р)/Х(Р)= W₁(Р)+ W₂(Р)+…+ W_n(Р)= W(Р)

Передаточная функция АСР состоящая из n параллельно соединенных звеньев равна сумме передаточных функций отдельных ее звеньев.

3.3.3 Соединение звеньев по принципу обратной связи

Схема замкнутого АСР приведена на рис.3

Х

W₁(P)

Х₊₊

(Р) Х₁ У(Р)

Х_ос(Р) W(P)

+1

W₁(P) м.б. последовательное соединение различных звеньев, параллельное и т.д.В любом замкнутом АСР сигнал с ее выхода по каналу обратной связи поступает на ее вход. Если по направлению данный сигнал обр. связи Х_ос(Р) совпадает с основным Х(Р), то такая связь называется положительной. В этом случае результирующий сигнал системы Х₁(Р) равен сумме данных сигналов, т.е Х₁(Р)= Х(Р)+ Х_ос(Р)

Положительные обратные связи применяются только в качестве внутренних обратных связей, охватывающих только

Если сигнал обратной связи Х_ос(Р) направлен противоположно основному сигналу Х(Р) то такая обратная связь называется отрицательной.(рис.4)

Х

W₁(P)

Х₊₊

(Р) Х₁ У(Р)

Х_ос(Р) W(P)

-1

Суммарный сигнал Х₁(Р) равен разности основного сигнала Х(Р) и Х_ос(Р)

Х₁(Р)= Х(Р)- Х_ос(Р)

Для вывода передаточной функции рассмотрим вариант, когда в цепь включено звено с передаточной функцией W₂(P).(рис.5)

Х

W₁(P)

Х₊₊

(Р) Х₁ У(Р)

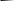
Х_ос(Р) W(P)

W₂(P)

Выходной сигнал У(Х) относительно передаточной функции W₁(P),а входной – Х₁(Р). У(Р)= W₁(Р)* Х₁(Р)

Х₁(Р)= Х(Р)- Х_ос(Р)

Х_ос(Р)= W₂(Р)*У(Р)

У(Р)= W₁(Р)[ Х(Р)- Х_ос(Р)]= W₁(Р)[ Х(Р)- W₂(Р)*У(Р)]

У(Р) + W₁(Р) *У(Р) W₂(Р)= W₁(Р)* Х(Р)

W(Р)= У(Р)/Х(Р)= W₁(Р)/1+ W₁(Р)* W₂(Р)

Для положительной обратной связи :

W(Р)= У(Р)/Х(Р)= W₁(Р)/1- W₁(Р)* W₂(Р)

Для АСР изображенном на рис.3 W₂(Р)=1, поэтому передаточная функция им.вид:

W(Р)= W₁(Р)/1– W₁(Р)

Для рис.4:

W(Р)= W₁(Р)/1+ W₁(Р)

3.4 Анализ точности АСР При определении точности АСР находят значение статической ошибки работы АСР (Δу).

Пример: определим статическую погрешность АСР, состоящей из последовательно – соединенных звеньев (безинерционного, инерционного, колебательно–затухающего), охваченных отрицательной обратной связью:

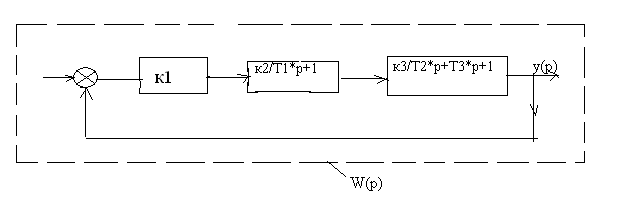
Получим придаточную функцию данного АСР:

W(р)= ,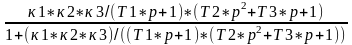

Преобразуем:

W(р)=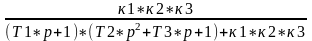 , Рассмотрим статический режим, приняв р=0 (оператор):

W(р)=у установится ≥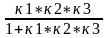 , Введем обозначения: к0=к1*к2*к3 – общ коэффициент усиления АСР, у установ-ся=к0/1+к0=1 – 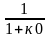, В данном случае принимаем задан значение выходной величины у=1, у задан =1. Статическая погрешность Δу определяется:

Δу=у задан – установится, Δу=1/1+к0 – статическая ошибка работы АСР. Ее можно уменьшить, увеличив…

3.5 Устойчивость АСР Чтобы АСР нормально работала она должна быть устойчивая. Устойчивость АСР – способность возвращаться к установившемуся положению (установленное значение регулируемой величины после прекращения действия возмущения которое вывело её из данного установившегося положения). Для оценки устойчивости работы АСР применяют 1) Алгебраический критерий Гурвиц и Раус.2)Частотные критерии Найквиста и Михайлова

Критерий Гурвица –основан на анализе неравенств состоящих из коэффициентов уравнения АСР. Характеристическое уравнение n-порядка

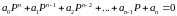
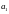
Оценка устойчивости АСР n-порядка по критерию Гурвица производится:составляется из коэффициентов характеристического уравнения Таблица Гурвица – по главной диагонали выписываются ; строка таблицы с нечетным и чётными индексами чередуются; число элементов каждой строки = n, недостающие коэффициенты заполняются нулями; отчеркивая строки и столбцы получают n определителей Гурвица. АСР n-порядка является устойчивой если все 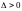( 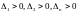) . Устойчивость АСР оценивается по 2-м условиям 1) - Необходимо положительно всех коэффициентов характеристического уравнения 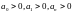2) – Достаточным является выполнение неравенств для определённого порядка АСР

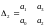
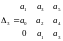
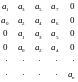
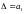
Условия получения положительного определителя Гурвица:

АСР 2-го порядка 1. 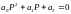Достаточное условие устойчивости АСР является положительность коэффициентов характеристического уравнения. АСР 3-го n=3 достаточное условие 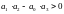. АСР 4-го n=4 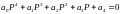достаточное условие