3 Основы теории автоматического регулирования

3.1.1Дифференциальные уравнения (обыкновенные)

у - выходная переменная АСР, х - входная, dt - динамика АСР. Для решения уравнения применяют операционное исчисление основанные на преобразовании Лапласа.

3.1.2 Передаточные функции

Преобразование Лапласа имеет следующий вид

гдн - аргумент, - изображение данного аргумента , - некоторая переменная которая называется переменная Лапласа. Свойства преобразования при начальных нулевых значениях т.е. t=0 x(t)=0

1) , , 2) , 3) , , 4) , где L-преобразование

Преобразование по Лапласу с использованием его свойств

возьмем отношение

Отношение преобразуем по Лапласу выходной величины АСР или линейно к преобразованной по Лапласу входной величины элемента называется передаточной функцией АСР или элемента. Знаменатель передаточной функции = 0, называется характеристическим уравнением АСР

3.2 Управления типовых звеньев аср

3.2.1 Назначение и классификация типовых звеньев Любая АСР состоит из элементов или звеньев объединенных в схему при этом динамическая АСР зависит из динамических характеристик звеньев и способов соединения их в звенья их в звенья образующих АСР. Поэтому для получения динамических характеристик всей АСР нужно знать характеристики всех ее элементов. Объектов регулирования, датчиков, регуляторов и др.Все элементы АСР по своим динамическим характеристикам, т.е по зависимости выходной величины можно классифицировать на следующие типовые звенья:-безинерционные (усилительные);-инерционные (аппериодическое звено 1-го порядка);-интегрирующая(астатическое звено 1-го порядка);-дифференцирующие звенья;-колебательно затухающее звено;-аппериодическое звено 2-го порядка;-звено чистого запаздывания.

3.2.2 Безинерционное звено (усилителительное) Динамическая характеристика имеет вид: y=k x (3.2.1)

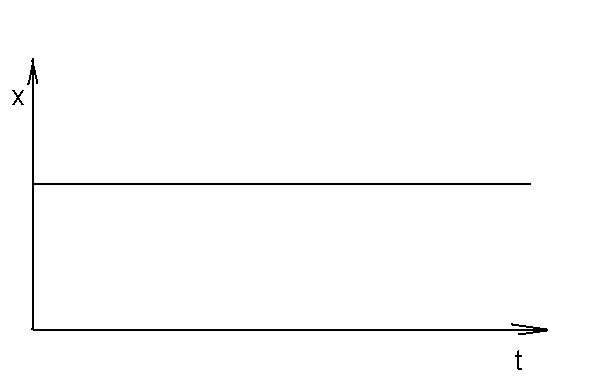
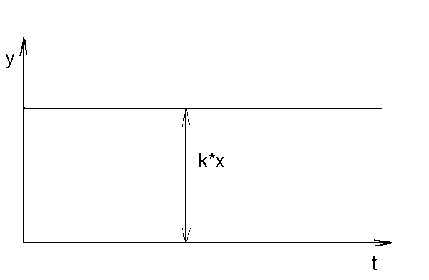
Преобразуем уравнения по Лапласу y(p)=k x(p)

W(p)= (3.2.2)

Пример данного звена- n-регулятор, все усилители,рычаги.

3.2.3 Инерционное звено Динамическая характеристика такого звена имеет вид: T (3.2.3),T - постоянное времени, к - коэффициент усиления. x-const; y= (3.2.4)

По формуле(3.2.4) построим графики переходного процесса:

; ;

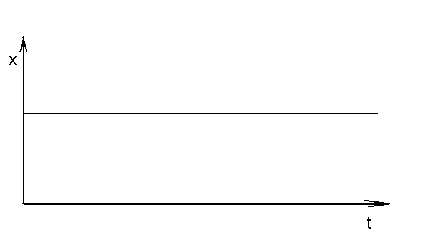
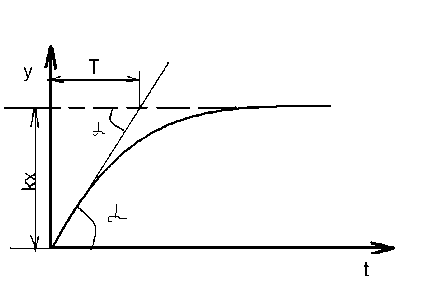
Для этого (3.2.3)преобразуем по Лапласу:

(3.2.5)

Одноемкостные статические объекты: термопары, мембрано-исполнительный механизм. Данное звено называется аппериодическим звеном 1-го порядка.

3.2.4 Интегрирующее звено Динамическая характеристика: Т*dy/dt=к*х.Преобразуем: dy/dt=к*х/Т, ,Проинтегрируем: y-y0=к/Т* , х=cоnst, y=кх/Т*t+y0.График переходного процесса:

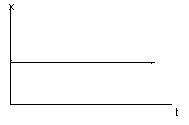
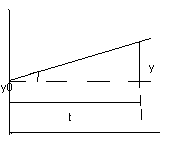
y/t=кх/Т=tgα, α=аrctgк*х/Т. Получим функцию звена, преобразуем по Лапласу: Т*р*y(р)=к*х(р), W(р)=y(р)/х(р)=к/Т*р. Данное звено называется астатическим звеном 1-го порядка (емкостные астатические объекты, интегральные регуляторы).

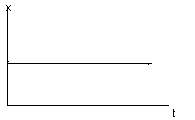
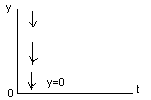
3.2.5 Дифференцирующие звенья делятся на реальные и идеальные. Динамическая характеристика идеального дифференцирующего звена имеет вид: y=к*dх/dt (При t=0, y ; при t , у=0)

Получим передаточную функцию звена: у(р)=к*р*х(р), W(р)=у(р)/х(р)=к*р.Пример:1.Электрический контур, в котором протекает ток и имеется напряжение, тогда ток в контуре будет равен: i=c*dUвых/dt,2.Трансформеры напряжения: Uвых=к*dФ/dt, Ф=к1*i1 (величина потока соз-ся в сердечнике i1). Uвых=к2*di1/dt (вых. напряжение).

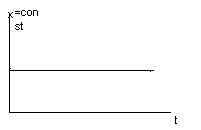
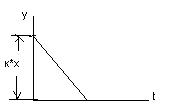
Динамическая характеристика реального дифференцирующего звена им вид: Т*dy/dt+y=k*dx/dt (при t=0, y , при t , y=k*x*e^-t/T

Получим передаточную функцию: Т*р*у(р)+у(р)=к*р*х(р), W(р)=к*р/(Т*р+1).Пример: электрический контур, содержащий емкость С и сопротивление R. Получим: R*c*Uвых/dt+Uвых= dUвых/dt – закон Киркгофа. Дифференцирующие звенья широко применяются в АСР и способствует устойчивой ее работе.

3.2.6 Колебательное затухающее звено, апериодическое звено 2-го порядка Это такое звено, у которого при скачкообразном изменении х, выходная величинана – у изменится в колебательном режиме с постоянным периодом и с амплитудой затухающего колебания по экспоненте. Динамическая характеристика имеет вид: Т0²*d²y/dt²+T*dy/dt+y=к*х. Это уравнение 2-го порядка, звено имеет 2 емкости – Т0 и Т. Для решения уравнения необходимо получить передаточную функцию и характерное уравнение для данного звена. Передаточная функция: Т0²*р0²*у(р)+Т*р*у(р)+у(р)=к*х(р)

W(р)=у(р)/х(р)=к/(Т0²*р²+Т*р+1). Характерное уравнение (когда знаменатель=0): Т0²*р²+Т*р+1=0.

Найдем корни: Р1,2=-Т/(2*Т0²)± (Т²-4Т0²/4*Т0⁴). Данные корни могут быть комплексно-сопряженные или действительно отрицательные. Если Т<2Т0, то корень дифференциала уравнения будет отрицательным и корни комплексно-сопряженные, т е: Р1,2=-α±j*ω. Коэффициент затухания α=Т/2Т0², ω= 4Т0²/Т0/4Т0⁴) – частота вынужденных колебаний выходной величины у. Решение будет иметь вид: у=у установится – с*е^-αt*sin(ω*t+ψ), где с, ω – постоянные интегрирования, которые определяются из начальных условий, т е: (dy/dt)_t=0. Параметры: у установится = к*х, с=к*х*(ω0/ω), ω0=1/Т0 – частота свободных колебаний выходной переменной, ψ=arctg(ω/α). Подставив все получим:

y=кх*[1 - ω0/ω*е^-αt*sin(ω*t+arctg ω/α)]. График переходного процессса (х=const):

Пример: двухъемкостные статические объекты, электродвигатели переменного тока (асинхронные).

Апериодическое звено 2-го порядка: Динамическая характеристика данного звена имеет вид:

Т0²*d²y/dt²+T*dy/dt+y=к*х. Характеристическое уравнение данного звена: Т0²*р²+Т*р+1=0. Соотношение постоянных времени имеет следующий вид: Т1>2Т0. Корни характеристического уравнения будут вещественными и отрицательными: Р1,2=-α±γ, α=-Т1/2Т0, γ= ((Т1²-4Т0²)/4Т0⁴). И решение исходного дифференциального уравнения имеет вид: у=к*х – с1*е^-(α+γ) – с2*е^{-( α-γ)}, где с1,с2 – постоянная интегрирования. График переходного процесса им s-вид: