
- •Линейные операции над векторами Сложение векторов
- •Вычитание векторов
- •Умножение вектора на число
- •Свойства линейных операций над векторами
- •Координаты вектора
- •Скалярное произведение
- •Векторное произведение векторов и его свойства
- •Уравнение прямой линии, проходящей через заданную точку перпендикулярно заданному направлению
- •Расстояние от точки до плоскости
Уравнение прямой линии, проходящей через заданную точку перпендикулярно заданному направлению
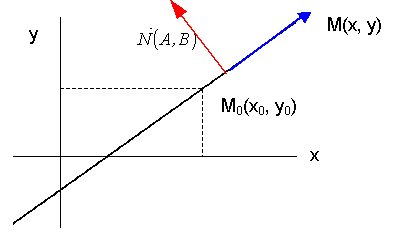
Пусть дана точка М0(x0, y0) и некоторый вектор N (A, B). Составим уравнение прямой линии, проходящей через данную точку и перпендикулярной заданному вектору. Для этого выберем произвольную точку М(x, y) на прямой. Тогда вектор
![]()
будет перпендикулярен вектору N (A, B). Записывая признак перпендикулярности векторов в координатной форме, получим A·( x - x0 ) + B·( y - y0 ) = 0. Раскрывая скобки, получим общее уравнение прямой линии на плоскости
A·x + B·y + C = 0,
где С = − А·x0 − B·y0. Из этого уравнения виден смысл коэффициентов А и В – они являются координатами вектора, перпендикулярного прямой (являются координатами нормального вектора).
Уравнение прямой, проходящей через две точки: A(x1, y1) и B(x2, y2), записывается так:
![]()
![]()
![]()
![]()
№13
Расстояние точки A(x1, y1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле
![]()
![]()
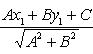
![]()
Где
![]()
![]() ,
взятый со знаком, противоположным знаку
свободного члена C.
,
взятый со знаком, противоположным знаку
свободного члена C.
№14
Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменными х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называются текущими координатами точек поверхности.
Уравнение сферы
Найдем
уравнение сферы радиуса R с центром в
точке O1(x0;y0;z0).
Согласно определению сферы расстояние
любой ее точки М(х; у; z) от центра
O1(x0;y0;z0)
равно радиусу R, т. е. O1M=
R. Но ![]() ,
где
,
где ![]() .
Следовательно,
.
Следовательно,
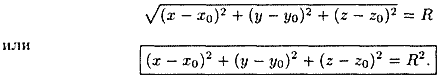
Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.
Если
центр сферы Ο1 совпадает
с началом координат, то уравнение сферы
принимает вид ![]() .
.
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
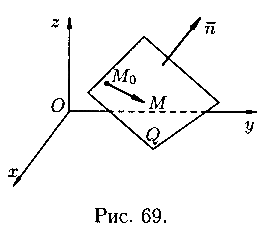
Пусть
в пространстве Oxyz плоскость Q задана
точкой ![]() и
вектором
и
вектором ![]() ,
перпендикулярным этой плоскости (см.
рис. 69). Выведем уравнение плоскости Q.
Возьмем на ней произвольную точку
,
перпендикулярным этой плоскости (см.
рис. 69). Выведем уравнение плоскости Q.
Возьмем на ней произвольную точку ![]() и
составим вектор
и
составим вектор ![]() .
При любом расположении точки Μ на
плоскости Q векторы
.
При любом расположении точки Μ на
плоскости Q векторы ![]() и
и ![]() взаимно
перпендикулярны, поэтому их скалярное
произведение равно нулю:
взаимно
перпендикулярны, поэтому их скалярное
произведение равно нулю: ![]() ,
т. е.
,
т. е.
![]()
Уравнение плоскости, проходящей через три данные точки
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M1(x1;y1;z1), М2(x2;y2;z2) и М3(х3,y3,z3), не лежащие на одной прямой.
Возьмем
на плоскости произвольную точку M(x;y;z)
и составим векторы ![]() ,
, ![]() ,
,![]() .
Эти векторы лежат на плоскости Q,
следовательно, они компланарны. Используем
условие компланарности трех векторов
(их смешанное произведение равно нулю),
получаем
.
Эти векторы лежат на плоскости Q,
следовательно, они компланарны. Используем
условие компланарности трех векторов
(их смешанное произведение равно нулю),
получаем ![]() ,
т. е.
,
т. е.
 (12.6)
(12.6)
№15
Расстояние от точки до плоскости
Предложение
11 . 1 Пусть плоскость ![]() задана
уравнением
задана
уравнением![]() и
дана точка
и
дана точка ![]() .
Тогда расстояние
.
Тогда расстояние ![]() от
точки
от
точки![]() до
плоскости
определяется
по формуле
до
плоскости
определяется
по формуле 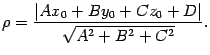 (
11 .7)
(
11 .7)
 Доказательство.
Расстояние от точки
до
плоскости
--
это, по определению, длина перпендикуляра
Доказательство.
Расстояние от точки
до
плоскости
--
это, по определению, длина перпендикуляра ![]() ,
опущенного из точки
на
плоскость
(рис. 11.9). Расстояние
от точки до плоскости.
,
опущенного из точки
на
плоскость
(рис. 11.9). Расстояние
от точки до плоскости.
Рис. 11 . 9
Вектор ![]() и
нормальный вектор n плоскости
параллельны,
то есть угол
и
нормальный вектор n плоскости
параллельны,
то есть угол ![]() между
ними равен 0 или
между
ними равен 0 или ![]() ,
если вектор n имеет направление
противоположное, указанному на рис.
11.9. Поэтому
,
если вектор n имеет направление
противоположное, указанному на рис.
11.9. Поэтому ![]() Откуда
Откуда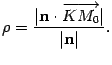 (
11 .8) Координаты точки
(
11 .8) Координаты точки ![]() ,
которые нам неизвестны, обозначим
,
которые нам неизвестны, обозначим![]() .
Тогда
.
Тогда ![]() .
Так как
.
Так как ![]() ,
то
,
то![]() .
Раскрыв скобки и перегруппировав
слагаемые, получим
.
Раскрыв скобки и перегруппировав
слагаемые, получим![]() (
11 .9) Точка
лежит
на плоскости
,
поэтому ее координаты удовлетворяют
уравнению плоскости:
(
11 .9) Точка
лежит
на плоскости
,
поэтому ее координаты удовлетворяют
уравнению плоскости:![]() .
Отсюда находим, что
.
Отсюда находим, что ![]() .
Подставив полученный результат в
формулу ( 11.9 ), получим
.
Подставив полученный результат в
формулу ( 11.9 ), получим![]() .
Так как
.
Так как ![]() ,
то из формулы ( 11.8 ) следует формула (
11.7 ).
,
то из формулы ( 11.8 ) следует формула (
11.7 ).
№16
Параметрические уравнения прямой
Замечая,
что ![]() ,
, ![]() ,
, ![]() ,
уравнение (12.11) можно записать в виде
,
уравнение (12.11) можно записать в виде
![]()
Отсюда следуют равенства:
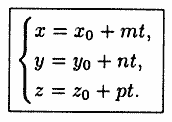 (12.12)
(12.12)
Они называются параметрическими уравнениями прямой в пространстве.
Канонические уравнения прямой
Пусть ![]() —
направляющий вектор прямой L и
—
направляющий вектор прямой L и ![]() -
точка, лежащая на этой прямой. Вектор
,
соединяющий точку М0 произвольной
точкой
прямой
L, параллелен вектору
-
точка, лежащая на этой прямой. Вектор
,
соединяющий точку М0 произвольной
точкой
прямой
L, параллелен вектору ![]() .
Поэтому координаты вектора
.
Поэтому координаты вектора ![]() и
вектора
пропорциональны:
и
вектора
пропорциональны:
 (12.13)
(12.13)
Уравнения (12.13) называются каноническими уравнениями прямой в пространстве.
Замечания:
1) Уравнения (12.13) можно было бы получить сразу из параметрических уравнений прямой (12.12), исключив параметр t. Из уравнений (12.12) находим
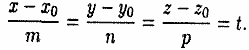
У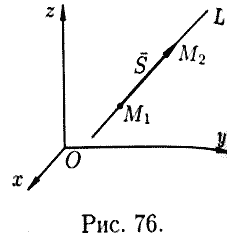 равнение
прямой в пространстве, проходящей через
две точки
равнение
прямой в пространстве, проходящей через
две точки
Пусть
прямая L проходит через точки ![]() и
и ![]() .
В качестве направляющего вектора
можно
взять вектор
.
В качестве направляющего вектора
можно
взять вектор ![]() ,
т.е.
,
т.е. ![]() (см.
рис. 76). Следовательно,
(см.
рис. 76). Следовательно, ![]() ,
, ![]() ,
,![]() Поскольку
прямая проходит через точку
,
то, согласно уравнениям (12.13), уравнения
прямой L имеют вид
Поскольку
прямая проходит через точку
,
то, согласно уравнениям (12.13), уравнения
прямой L имеют вид
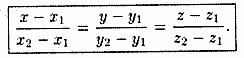 (12.14)
(12.14)
Уравнения (12.14) называются уравнениями прямой, проходящей через две данные точки.
