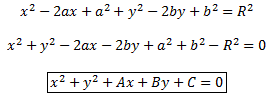Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов   и любых действительных чисел   справедливы равенства:

Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.

№4

Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).

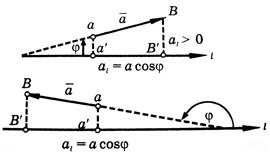
Проекция вектора   на ось   обозначается через a_l или  , а угол между осью   и вектором   будем обозначать так:  . Таким образом,

     (2)

Свойства проекций вектора на ось

№5

Суммой векторов

и

называется вектор

,

т.е. при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются.

Произведением вектора

на действительное число   называется вектор

т.е. при умножении вектора на число каждая его координата умножается на это число.

№6

Координаты вектора

Пусть вектор   имеет началом точку А( х_а, у_а) и концом точку В( х_b, y_b). Координатами вектора   будем называть числа АВ_х = х_b - х_а, АВ_у = у_b - у_а, АВ_z = z_b - z_а.

№7

 Если x₁ и y₁ - координаты точки A, а x₂ и y₂ - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении  , определяются по формулам

Если  , то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам

№8

Скалярное произведение

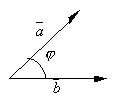      Скалярное произведение векторов    и  : 

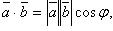
где   - угол между векторами   и  ; если   либо  , то 

     Из определения скалярного произведения следует, что   где, например,   есть величина проекции вектора   на направление вектора  .

     Скалярный квадрат вектора: 

     Свойства скалярного произведения:             

     Скалярное произведение в координатах 

  Если     то   

     Угол между векторами 

       

№9

Векторное произведение векторов и его свойства

В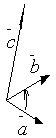 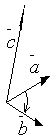ведем сначала понятие ориентации тройки векторов.

Пусть даны три некомпланарных вектора   с общим началом, перечисленных в определенном порядке: первый –  , второй –  , третий –  .

Тройка некомпланарных векторов   называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройку векторов называют левой, в этом случае если мы будем смотреть с конца вектора  , то кратчайший поворот от   к   осуществляется по часовой стрелке.

Векторным произведением векторов   и  называется новый вектор  , удовлетворяющий условиям:

1. Д 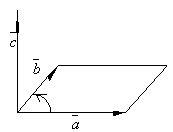лина вектора   равна площади параллелограмма, построенного на векторах   и  .

2. Вектор   перпендикулярен плоскости этого параллелограмма.

3. Он направлен так, что векторы   и   образуют правую тройку векторов.

Векторное произведение векторов   и   обозначается символом  . Если хотя бы один из сомножителей равен нулю, то векторное произведение по определению считают равным нулю

Векторное произведение обладает следующими свойствами:

1. Из определения следует, что длина векторного произведения численно равна площади параллелограмма, построенного на векторах, и, следовательно, находится по формуле:

.

Таким образом,   и  .

2. При перестановке сомножителей векторное произведение меняет свой знак  .

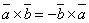Д ействительно из определения векторного произведения следует, что векторы   и   имеют одинаковые модули, расположены на одной прямой, но направлены в противоположные стороны. Поэтому, векторы   и   являются противоположными векторами и поэтому  .

3. Скалярный множитель можно выносить за знак векторного произведения, т.е. для любого числа λ и любых векторов 

.

Доказательство этого свойства непосредственно следует из определения векторного произведения. Докажем для λ > 0. В этом случае  . Тогда по определению векторного произведения

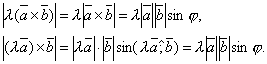
Вектор   перпендикулярен векторам   и  . Вектор   также   векторам   и  , т.к. векторы   и  ,   и   лежат в одной плоскости. Следовательно, векторы   и  коллинеарны. Очевидно, что направления их также совпадают. Т. к.  , и следовательно,  , то  .

Поэтому  .

Аналогично проводится доказательство для случая λ < 0.

4. Для любых векторов   имеет место равенство

.

Примем без доказательства.

5. Векторное произведение двух векторов равно нулевому вектору тогда и только тогда, когда один из сомножителей равен нулю или векторы коллинеарны.

Действительно, если векторы коллинеарны, то  , т.е. площадь параллелограмма, построенного на данных векторах,равна нулю.

Таким образом, для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.

В частности  .

№10

Смешанным произведением трёх векторов   называют число, равное  . Обозначается  . Здесь первые два вектора умножаются векторно и затем полученный вектор   умножается скалярно на третий вектор  . Очевидно, такое произведение есть некоторое число.

Рассмотрим свойства смешанного произведения.

1. Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е.  .

Таким образом,   и  .

Д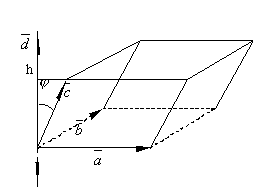 оказательство. Отложим векторы   от общего начала и построим на них параллелепипед. Обозначим   и заметим, что  . По определению скалярного произведения

. Предполагая, что  и обозначив через h высоту параллелепипеда, находим  .

Таким образом, при 

Если же  , то   и  . Следовательно,  .

Объединяя оба эти случая, получаем   или  .

Из доказательства этого свойства в частности следует, что если тройка векторов   правая, то смешанное произведение  , а если   – левая, то  .

2. Для любых векторов  ,  ,   справедливо равенство

.

Доказательство этого свойства следует из свойства 1. Действительно, легко показать, что   и  . Причём знаки "+" и "–" берутся одновременно, т.к. углы между векторами   и   и   и   одновременно острые или тупые.

3. При перестановке любых двух сомножителей смешанное произведение меняет знак.

Действительно, если рассмотрим смешанное произведение  , то, например,   или

.

4. Смешанное произведение 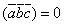  тогда и только тогда, когда один из сомножителей равен нулю или векторы   – компланарны.

 

Доказательство.

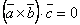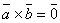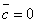1. Предположим, что  , т.е.  , тогда   или   или  .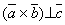

Если  , то   или   или  . Поэтому   – компланарны.

Если  , то  ,  ,   - компланарны.

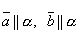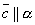2. Пусть векторы   – компланарны и α – плоскость, которой они параллельны , т. е.   и  . Тогда 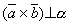 , а значит  , поэтому 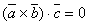  или  .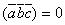

Т.о., необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Кроме того, отсюда следует, что три вектора   образуют базис в пространстве, если  .

Если векторы заданы в координатной форме  , то можно показать, что их смешанное произведение находится по формуле:

.

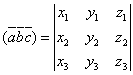Т. о., смешанное произведение  равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.

Все по векторам: http://examen.nx0.ru

http://tvsh2004.narod.ru/vekt.html

№11

Условие коллинеарности двух векторов.

Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны. Т.е. если  , то .

Доказательство:

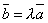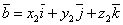1. Пусть вектор   коллинеарен  , тогда найдется λ такое, что  . Значит,   и 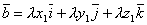 . Поскольку разложение вектора по элементам базиса 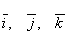  единственно, то  .

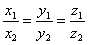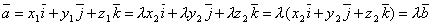2. Пусть выполняется равенство  . Обозначим коэффициент пропорциональности через λ. Тогда   и, следовательно,  , т.е.  . Теорема доказана.

Компланарность трех векторов.

Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.

Условие ортогональности векторов:

*-// Для двух векторов

№12

Уравнением линии называется уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линии и только они.

Входящие в уравнение линии переменные x и y называются текущими координатами, а буквенные постоянные - параметрами.

Окружность – множество всех точек плоскости, равноудаленных от данной точки на плоскости.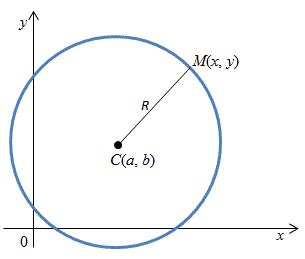

Выведем уравнение окружности.

Пусть C(a, b) – центр окружности, а R – ее радиус. Возьмем произвольную точку M(x, y) ∈  окр.

Расстояние от центра окружности до точки M находится по известной формуле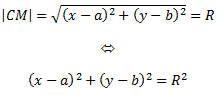

Каноническое уравнение окружности. В центре с координатами a и b и радиусом R

Если в этом уравнении раскрыть скобки и выполнить некоторые преобразования, то получим: