- •1.Основные понятия и определения автоматики. Сау- ее схема, элементы
- •2 Направления автоматизации тп пищ. Производств
- •3. Классиф-я автоматических средств управления
- •4 Методы измерений и ошибки измерения (статическая, динамическая)
- •5 Средства измерений и контроля в автоматике
- •6 Государственная система приборов (гсп) и средств автоматизации
- •7 Общие сведения о датчиках
- •8 Датчики температуры
- •9 Датчики давления и разрежения
- •10 Датчикии расхода и количества вещества
- •11. Преобразователи параметров движения
- •12. Методы и устройства измерения состава и свойств в-в
- •13 Общие сведения об усилительных устройствах в автоматике
- •14. Электромеханические и магнитные усилители
- •15 Электронные усилители (эу)
- •16 Гидравлические и пневматические усилители(гу и пу)
- •17. Общие сведения об исполнительных механизма
- •18. Гидравлические и пневматические им
- •19. Электрические им
- •20. Регулирующие органы
- •21. Ро объемного, скоростного, дроссельного типа
- •22. Математическое описание элементов и систем автоматики в статическом режиме
- •23. Динамический режим работы сар, динамические хар-ки: временные и частотные
- •24. Типовые входные воздействия и хар-ки сар- временные, частотные, передат. Ф-ция
- •25. Типовые звенья сар: пропорциональные, идеальные интегрирующее и дифференцирующее, их хар-ки
24. Типовые входные воздействия и хар-ки сар- временные, частотные, передат. Ф-ция
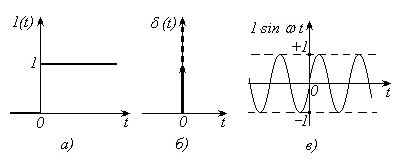
В кач-ве типовых вх. воздействий исп. простые для матем. описания функции: единичную функцию, дельта – функцию и гармоническое колебание.
Единичная
функция
(ступенчатая функция, единичный скачок),
это ф-ция вида

График этой функции приведен на рис.6.2, а.
Дельта
– функция
(
- функция)
- это импульс бесконечно мал. длительности
и бесконечно больш. амплитуды, для к-го
выполняется усл.
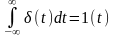 .
Очевидно, что
.
Очевидно, что
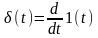 .
Аналитически записываю
.
Аналитически записываю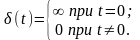
График дельта - функции приведен на рис. 6.2, б.
Гармоническое
колебание,
(рис.2, в)
это колебание вида 1sin
t
или
1cos
t,
где
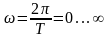 .
.
|
Рис. 6.2. Типовые входные воздействия:
|
В комплексной форме гармонич. колебание запис. в виде 1 e j t =1(cos t+j sin t).
По определению, все 3 сигнала явл-ся безразмерными. Однако если любой из них умножить на единичное знач. конкретного физ. параметра, то тогда типовой сигнал приобретает размерность.
Временные хар-ки исп. 2 временные хар-ки – переходную и импульсную.
Переходной хар-кой h(t) элемента или сис-мы назыв. ее реакцию на единичную функцию (Рис. 6.3, а). Экспериментально снятую перех. Хар-ку наз. кривой разгона. Импульсной характеристикой g(t) , наз. реакцию элемента (системы) на вх. воздействие в виде дельта – функции (Рис. 6.3, б).
|
|
Частотные хар-ки Если в кач-ве вх. воздействия исп-ся гармоническое колебание, то получ. частотные хара-ки. При усл. линейности элемента (системы), применив комплексный метод, на выходе (Pис.6.4, а) получим комплексную, или амплитудно-фазовую характеристику (АФХ), к-ю обозн. К(j). Выражение К(j) можно представить в показательной форме, как К(j)= К()e j t,
где К() – амплитудно-частотная хар-ка (АЧХ); () – фазочастотная хар-ка (ФЧХ).
|
Передаточная функция элемента(системы) наз. отнош изображения вых. велич. к изображению вх.велич.
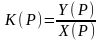 ,
где Y(P),
X(P)
– изображения по Лапласу функций
времени y(t)
и x(t).
,
где Y(P),
X(P)
– изображения по Лапласу функций
времени y(t)
и x(t).
Использ.
преобразований Лапласа лежит в основе
операцион. исчисления. Прямое преобразов.
Лапласа позволяет перейти от диф.
уравнений к алгебраическим за счет
того, что операцию дифференцирования
функций времени (оригиналов) можно
заменить умножением их изображений на
оператор р
в соотв. степени, т. е.
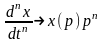 .
.
Дифф. уравнения превращаются в алгебраические, к-е легко решаются. От решений, получ. в операционной форме, с пом. обратного преобразования Лапласа (или по таблицам) находят оригиналы, напр. функцию y(t).
При известной передаточной функции системы, изображение Y(р) = К(р) X(р), т. е. легко опр-ся.
М/ду функциями времени и их изображениями сущ. предельные соотношения, к-е полезны при проверке вычислений с пом. преобразований Лапласа.
Первое
предельное соотношение: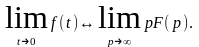 .
.
Оно позв. определить нач. знач-е функции f(t) при t = 0 непосредственно по изображению F(p).
Второе
предельное соотношение:
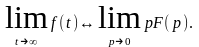
Оно дает возм-ть найти предел функции f(t) при t→ ∞ по знач. ее изображения F(p) в нач. координат, при р = 0.