Вопрос 42. Производная показательно-степенной ф-ции.

Ф-ция фида у=[u(x)]^V(x) наз-ся показательно-степенной фун-й.

Производная функции находится по правилу логарифмируемого диф-ла.

1) Логар-ем Ln y=ln*u^V ; ln y=V*ln*u. 2) Диф-м (ln y)`=(V*ln*u)`,

считая у-сложной ф-ей. 1/y*y`=V`(x)*ln*u(x)+(ln*u(x))`V(x) домножаем на *y=u^V.

y`=u^V(V`*ln*u+1/u u`*V)-производная показат-степ ф-ции.

Вопрос 43. Дифференцир-е неявной ф-ции,

и ф-ции заданной параметрически

Если функция задана уравнением у = f(х), разрешенным относи­тельно у,

то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции

в виде уравнения F(x; у) = 0, не разрешенного относительно у.

Всякую явно заданную функцию у = f(x) можно записать

как неявно заданную уравнением f(x) - у = 0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение от­носительно

у (например, y + 2x + cosy-l = 0 или 2^y-x+y=0). Если неявная функция задана

уравнением F{x;у) = 0, то для нахо­ждения производной от у по х нет

необходимости разрешать урав­нение относительно у: достаточно

продифференцировать это уравнение по х, рассматривая при этом у как функцию х,

и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

Задана параметрически: Пусть зависимость между аргументом х и

функцией у задана параметрически в виде двух уравнений:

(1). где t — вспомогательная переменная,

называемая параметром.

Найдем производную считая, что функции (1) имеют

произ­водные и что функция х = x(t) имеет обратную .

По правилу дифференцирования обратной функции: .

Функцию у=f(x), определяемую параметрическими уравнения­ми (1),

можно рассматривать как сложную функцию у = y(t), где .

По правилу дифференцирования сложной функции имеем: .

С учетом равенства (2) получаем: .

Полученная формула позволяет находить производную

от функции заданной параметрически, не находя

непосредственной зави­симости у от х.

Вопрос 44. Дифференциал функции.

Геометрический смысл.

Дифференциал функции y=f(x) в точке Хо наз-ся главное

линейное отношение аргумента ∆х часть приращения ф-ции ∆у.

Обозначим dy. dy= f `(Xo) ∆х.

Геометрический смысл = приращению ординаты касательной,

проведенной к графику ф-ции в точке Хо.

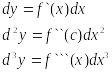
Вопрос 46. Теорема Ферма.

1) y=f(x) диф на [a,b] 2) пусть Е(наоборот)с, a<c<b f(c )

- наиб или наимен значение. Тогда f`(x)=0.

Док-во: пусть выполн-ся услов теоремы. ∆y=f(c+∆x)-f(c )<=0 наиб значение.

1) ∆y/∆x=f(c +∆x)-f(c )/∆x<=0, ∆x>0 2) y/∆x=f(c +∆x)-f(c )/∆x>=0, ∆x<0.

Раз в кажд точке то и в точке С.

E(наоборот)f `(x)=lim ∆x0 ∆y/∆x(∆x0 любым образом).

∆x+0=>1(над стрелкой)f `(c )<=0

∆x-0=>2(над стрелкой)f `(c )>=0 Эти выражения в фигур скобках =>f `(c )=0.

Теорема доказана.

Вопрос 47. Теорема Роля

теорема Ролля

если y=(x) 1)непрерывна на [a;b] 2) дифференцируема на ]a;b[ 3)f(a)=f(b)

тогда внутри [a;b] найдется хотя бы 1 точка с, такая ,что (c)=0 (a<c<b)

т.к. ф-я непрерывна на пр-ке ,то в силу т.веерштрасса на [a;b]

она достигает min и max значений ,причем min  max ,иначе ф-я яв-ся const .

допустим ,что m<M ,заметим,что ни одно из этих значений

ф-я не прнимает на концах интнорвала ибо в силу 3 усл-я теоремы m=M

допустим в (.)с (a<c<b) (с)=m т.к.

по 2 усл-ю ф-я диффер. в (.)с ,то она имеет односторонние

производные

_t=lim_{x0 x0}((x+x)-f(x))/x0 осуществ-я предельный

п ереход в нер-ве мы получили ₊(с) 0

_t=lim_{x0x0} ((x+x)-f(x))/x0 _-(с)0 по усл-ю

теоремы ф-я в любой (.) гр-ка диф-ма в т.ч. и в (.)с

₊(с)= _-(с)= (с) ,а это возможно только когда (с)=0

геометрический смысл если выполн. усл-я т. Ролля, то этозначит ,

что внутри [a;b] найдется хотябы 1 точка, касат. в которой будет || ох

если хотя бы 1 из условий теоремы не выполнено хотя бы в 1 точке,то т.

перестает быть справедливой