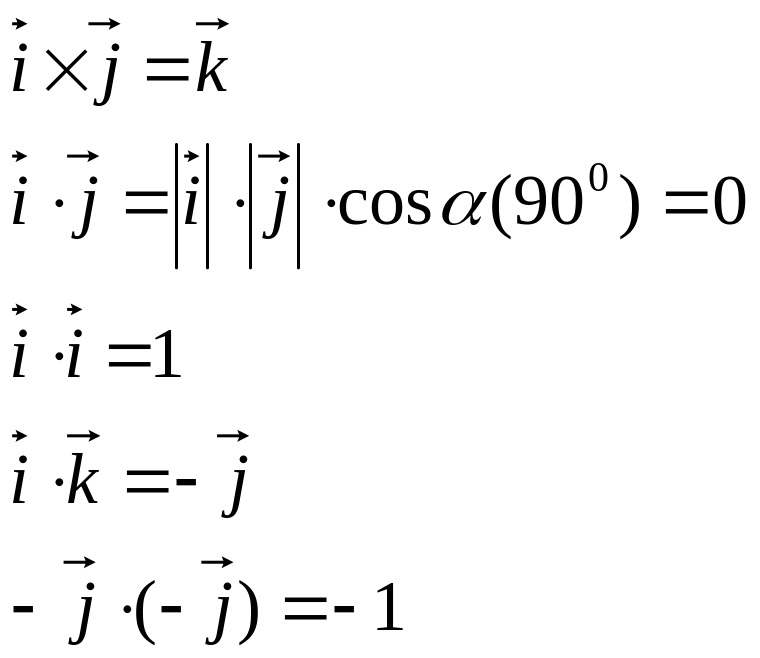- •Вопрос 12. Плоскость в пространстве.
- •13. Взаимное расположение пл-тей в пространстве.
- •Вопрос 14. Различные виды уравнений пл-ти.
- •1 Способ
- •2 Способ
- •1. Мб задана как линия пересечения 2х пл-тей
- •Вопрос 21. Эллипс.
- •Вопрос 27. Б.М.В и б.Б.В
- •Вопрос 41. Дифференцир-е обратной и сложной ф-ции.
- •Вопрос 42. Производная показательно-степенной ф-ции.
- •Вопрос 43. Дифференцир-е неявной ф-ции,
- •Вопрос 44. Дифференциал функции.
- •Вопрос 46. Теорема Ферма.
- •Вопрос 47. Теорема Роля
- •Вопрос 48. Теорема Лагранжа
- •Вопрос 49. Теорема Коши
- •Вопрос 50. Правило Лопиталя
- •Вопрос 32. Первый замечательный предел
- •Вопрос 34. Второй замечат предел
- •Вопрос 35. Сравнение бесконечно малых величин. Эквивалентные б.М.В.
- •Вопрос 37. Непрерывность ф-ции в точке и на отрезке.
- •Вопрос 31. Теоремы о переходе к пределу в неравенствах.
- •Вопрос 28. Св-ва бмв и ббв, связь между ними.
- •Вопрос 29. Теорема о связи предела ф-ции с бмв.
- •Вопрос 36. Односторонние пределы. Классификация точек разрыва.
- •Вопрос 38. Понятие производной.
- •Вопрос 24. Приведение общего ур-я кривой
- •Вопрос 23.
- •Вопрос 25. Приведение общего ур-я кривой
- •1. Поворот:
- •2. Параллел перенос.
- •Вопрос 26. Предел ф-ции.
- •Вопрос 20. Взаимное расположение прямых на плоскости.
- •Вопрос 45. Касательная и нормаль к кривой на пл-ти.
- •Вопрос 39.
- •Вопрос 40.
- •Вопрос 30.
- •Вопрос 22.
Вопрос 12. Плоскость в пространстве.
Теорема 1: В декартовых координатах
всякая пл-ть в пространстве определяется
уравнением 1 степени.
Док-во:
Р- плоскость. Mo(Xo;Yo;Zo)eP
(фиксированная точка)
N(вектор)=в
фиг скоб A;B;C![]() P(нормаль
к пл-ти)
P(нормаль
к пл-ти)
M(x;y;z)![]() P
(текущая точка)
P
(текущая точка)
Рассмотрим MoM(вектора). MoM(вектора) Р;
 -урав-е
первой степени.
-урав-е
первой степени.
Теорема 2: Всякое ур-е 1 степени относительно
декартовых координат точки в пространстве
определяет пл-ть.
Док-во: Рассмотрим Ах+Ву+Сz+D=0.
Пусть (Xo;Yo;Zo)- решение ур-ния
=> Ахо+Вуо+Сzо+D=0. => A(X-Xo)+B(Y-Yo)+C(Z-Zo)+D=0;
A(X-Xo)+B(Y-Yo)+C(Z-Zo)+D=0 ~ Ax+By+Cz+D=0
но A(X-Xo)+B(Y-Yo)+C(Z-Zo)+D=0
по Т1. определяет пл-ть проходящую
через
т.
![]()
![]() -общ
ур-е пл-ти ;
-общ
ур-е пл-ти ;
![]() -уравнение
пл-ти в отрезках ;
-уравнение
пл-ти в отрезках ;
1. D=0 =>Ax+By+Cz=0–плоскость проходящая
через начало коорд-т.2. А=О=>By+Cz+D=0 – пл.|| ОХ
3. B=0=>Ax+Cz+D=0 – пл.|| ОУ.4. С=О=>Ax+By+D-пл.|| OZ.
5.А=0;D=0=>By+Cz=0 – пл. проходящая через Ох
6. В=0;D=0=>Ax+Cz=0 – пл. проходящая через Оу.
7. С=0;D=0=>Ax+By=0 – пл. проход-ая через Оz.
8. A=B=0=>Cz+D=0 – пл.|| хОу
9. B=C=0=>Ax+D=0 – пл. || уОz. 1
0. A=C=0=>By+D=0 – пл.|| xOz. 11. A=B=D=0=>Z=0 – xOy
12. A=C=D=0=>y=0 – xOz. 13. B=C=D=>x=0 – yOz
14.
A;B;C;D![]() 0.
0.
13. Взаимное расположение пл-тей в пространстве.
Пл-ти в пространстве могут быть параллельными,
пересекающими и под прямым углом.
Пл-ти ||:

1.P1![]() P2.
Угол между
пл-ми наз двухгранный угол
P2.
Угол между
пл-ми наз двухгранный угол
который измеряется вписанном в него линейном уголом.
Этот линейный угол равен углу между
векторами нормалей этих пл-тей.
![]() или
или
![]()
2. P1 || P2
![]() Если
координаты нормали
Если
координаты нормали
пропорциональны то координаты пропорциональны.
Пусть пл-ти :
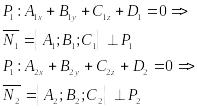
3. P1 P2
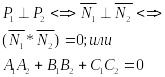
Условие пл-ти в пространстве.
Вопрос 14. Различные виды уравнений пл-ти.
1.
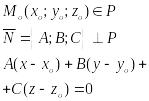
Ур-е пл-ти проходящее через т. Мо заданному вектору D.
2. М1(X1;Y1;Z1); M2(X2;Y2;Z2); M3(X3;Y3;Z3) P. M(x;y;z) P.
Рассмотрим:
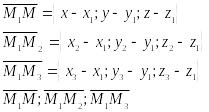
-комплонарные
вектора ![]()

Ур-е пл. проходящей через 3 заданные точки.
Замечание: Для получения ур-я пл-ти
нужно раскрыть определ. 1 строки.
3.

1 Способ

Выражает ур-е пл-ти проходящей через
заданную точку || 2м не комплонарным векторам.
2 Способ
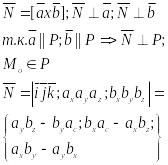
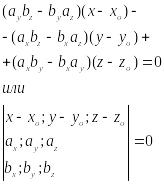
Вопрос 15. Расстояние от точки до пл-ти
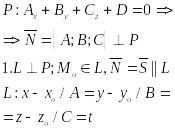
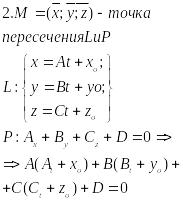
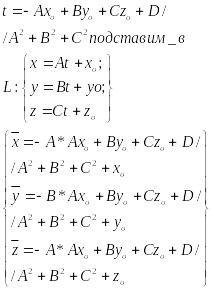

![]()
формула для нахождения расстояния от точки до пл-ти
Вопрос 16. Прямая в пространстве.
1. Мб задана как линия пересечения 2х пл-тей
![]() -Общее
ур-е прямой в пр-ве
-Общее
ур-е прямой в пр-ве
2.
![]() -направляющий
вектор прямой L
-направляющий
вектор прямой L
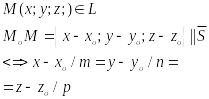
-каноническое ур-в прямой в пр-ве.
3.
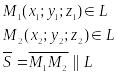
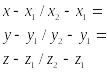
-ур-е прямой проходящей через 2 заданные точки
4.
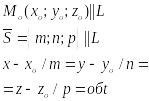


-параметрические ур-я прямой в пр-ве.
Вопрос 17. Взаимное расположение прямых в пр-ве.
Пусть
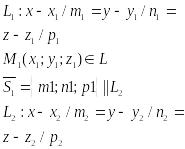

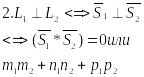
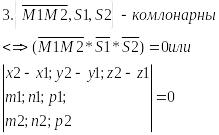
-условие пересечения 2х прямых
![]()
Если cos φ>0 то это острый угол, cos φ<0 то это тупой угол
![]()
Вопрос 18. Взаимное расположение
прямой и пл-ти в пространстве
![]()
Углом между L и P наз-ся угол между этой
прямой и ее проекцией на эту пл-ть.
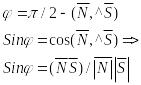
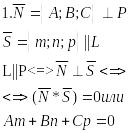
-условие параллельн.
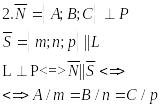
-условие перпендикулярности
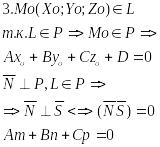
![]()
- условие L э P.
Вопрос 19. Прямая на плоскости
к![]() анонический
вид:
анонический
вид:
![]()
параметрический вид:
![]()
через две заданные точки:
с![]() угловым коэффициентом:
угловым коэффициентом:
Прямые перпендикулярны, если cos=1
Прямые параллельны, если k1=k2
Угол между прямыми:
![]()
Расстояние от точки до прямой:
![]()
Р![]() асстояние
от точки до плоскости:
асстояние
от точки до плоскости:
Плоскости параллельны:
![]()
Плоскости совпадают:
![]()
Плоскости перпендикулярны:
![]()
Направляющие косинусы вектора:
![]()
![]()
![]()
свойство:
![]()