16 .Сила давления ж на криволинейную стенку цилиндрич-й формы.

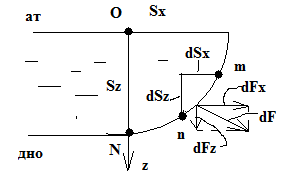
Сила давления ж на стенку явл-ся результатом взаимод-я жид-х частиц и смоченной пов-ти стенки. По з-ну равенства действия противодействия жид-ти на стенку гидростат-му давлению в ж на смоченной пов-ти стенки и направлена в противоположную сторону. Цилиндр-я стенка – это крив-я стенка, протяженная в одном направлении. 2Рис-ка. Будем рассматр-ть цилинд-ую стенку открытого сосуда. В этом случае стенка испытывает только избыточное давление от веса вышележащих слоев ж. р_изб=ρgz, z – глубина точки под СП. Атмосф-ое давление на внеш пов-ть стенки уравновеш-ся этим же давлением, к-е по з-ну Паскаля передается по свободной поверхности на смоченную пов-ть стенки. Начнем с опред-я силы давления на элементар-ю площадку dS. Принимая избыт-е давление в т. А в кч-ве среднего по элементар-й площадке dS находим: dF=р_{изб А}*dS=ρgz*dS, dF={dF_x,dF_z}, dF_x=dFcosα=ρgzdScosα=ρgzdS_z, dF_z=dFsinα=ρgzdSsinα=ρgzdS_x, Горизонтальную составляющую силу давления ж на стенку F_x найдем проссумировав по вертик-й проекции z по S_z: F_x= x=ρg ρgh_cS_z=p_{изб с}S_z, где S_z- площадь вертик-й проекции смоченной пов-ти стенки, h_с- расстояние от свободной пов-ти до центра тяжести площади S_z. F_x-гориз-я составляющая силы давления ж на стенку. F_x=р_{изб с}S_z (гориз-я) Гориз-я составляющая силы давления ж на стенку = сила давления на ее вертик-ю проекцию. Линия ее действия лежит ниже центра тяжести площади S_z. Вертик-я составляющая силы давления ж на стенку F_z представляет собой сумму всех элем-ых вертик-х составляющих dF_z, взятую по площади s_x, т.е по гориз-й пов-ти смоченной пов-ти. F_z= _z=ρg _x=ρg√, где √-объем ж, ограниченный смоченной пов-ю крив стенки, ее вертик-ой и гориз-ой проекциями. Жид-ть, заключенная в объеме √ наз-ся телом давления. Сила давления F_z= весу тела давления : F_z=ρg√=γ√ (вертик-я). Линия действия силы F_z проходит через центр тяжести объема √. Различают реальное тело давления и фиктивное тело давления. Если ж наход-ся над стенкой, то вертик-я составляющая силы давления F_z направлена сверху вниз, а тело давления опред-ся действительным объемом ж над стенкой и наз-ся реальным или положительным. Пример реального тела давления рис. Если ж наход-ся под стенкой, то вертик-я составляющая F_z направлена снизу вверх, а тело давления в этом случае соответствует фиктивному объему ж над стенкой и наз-ся фиктивным или отриц-ым. Пример. Рис. После нахождения составляющих F_x, F_z нужно путем геом-го суммирования найти равнодействующую силу

давления на крив стенку. F= , а также угол наклона этого вектора в гориз-й плоск-ти: α=arctg . Линия действия силы F проходит через точку пересечения линий действия составляющих F_x и F_z под углом α к гориз-ой плоск-ти. Рис.

17 .З-н Архимеда.

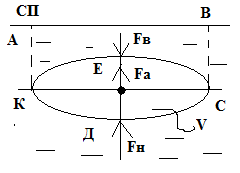
Рассмотрим однородное тело произвольной формы, полностью погруженное в жидкость. Пусть объем этого тела √_т. У однородного тела геометр-й центр и центр тяжести совпадают ГЦ=ЦТ. Рис. Поверхность тела разобьем на 2 части: верхнюю КЕС и нижнюю КДС. Будем рассматривать их как крив-е стенки, к-е испытывают давление от вышележащих слоев жид-ти. Гориз-е составляющие сил, действующие на эти пов-ти уравновешив-ся. Надо определить вертик-ю силу, к-е действуют на тело. Для этого воспольз-ся понятием тела давления. Для верх поверх-ти тело давления АВСЕКА, объемом √_В, явл-ся положит-ым. Вертик-я составляющая силы проходит через центр тяжести направлена сверху вниз. F_В=ρg√_В. Для нижн пов-ти тело давления АВСВКА, объемом √_н, явл-ся фиктивным или отриц-ым, вертик-я сила = F_н=ρп√_н=ρg(√_т+√_В) сила направлена снизу вверх.

F_н>F_В, F_A=F_н-F_В=ρgV_т, где F_А- сила Архимеда, она приложена в центре тяжести тела и точка приложения этой силы наз-ся центром водоизмещения.

На тело, погруженное в покоящуюся ж действует выталкивающая сила, направ-я вертик-но вверх и равная весу ж, вытесненной телом – з-н Архимеда. Тело имеет вес: 3случая: 1. F_A=G, тело плавает, наход-ся в равновесии, 2. F_A<G тело тонет, 3. F_A>G тело всплывает