Тема 5. Индексы

Пример 29

Имеются данные по одному из магазинов (таблица 29.1).

Таблица 29.1 – Объем реализации тканей по магазину

Вид ткани	Реализовано, тыс. м		Цена за 1 м, ден. ед.
	базисный период ( )	отчетный период ( )	базисный период ( )	отчетный период ( )
Хлопчатобумажные	15,0	13,8	2,8	3,1
Льняные	9,5	10,0	6,0	7,8

Определить:

1 Индивидуальные индексы физического объема, цен.

2 Сводные индексы объема реализации, цен и товарооборота.

3 Абсолютное изменение товарооборота общее и в результате изменения цен и физического объема реализованных товаров.

Сделать выводы.

Решение

1 Рассчитаем индивидуальные индексы физического объема и цен.

Индивидуальный индекс физического объема ( ) равен

.

или 92%, т. е. объем реализации хлопчатобумажной ткани в отчетном периоде снизился по сравнению с базисным на 8% (92 – 100).

или 105%, т. е. объем реализации льняной ткани в отчетном периоде увеличился по сравнению с базисным на 5% (105 – 100).

Индивидуальный индекс цен ( ) объема равен

.

или 111%, т. е. цена за 1 метр хлопчатобумажной ткани увеличилась в отчетном периоде на 11% (111 – 100).

или 130%, т. е. цена за 1 метр льняной ткани увеличилась в отчетном периоде на 30% (130 – 100).

2 Рассчитаем сводные индексы физического объема, цен и товарооборота.

Сводный индекс физического объема равен

или 99,6%.

Сводный индекс цен равен

или 122,4%.

Сводный индекс товарооборота равен

или 122%

или

или 122%.

3 Абсолютное изменение товарооборота ( ) составит

тыс. руб.

Абсолютное изменение товарооборота ( ) в результате изменения цен составит

тыс. руб.

Абсолютное изменение товарооборота ( ) в результате изменения физического объема реализованных товаров составит

тыс. руб.

Следовательно, товарооборот в отчетном периоде по сравнению с базисным вырос на 22% или на 22,78 тыс. руб. Это произошло за счет влияния двух факторов:

- за счет роста цен товарооборот вырос на 22,4% или на 22,14 тыс. руб.;

- за счет изменения объема реализованных товаров товарооборот снизился на 0,4% или на 0,36 тыс. руб.

Пример 30

Имеются данные о продаже товаров в торговых предприятиях района (таблица 30.1).

Таблица 30.1 – Объем товарооборота торговых предприятий района

Товар	Товарооборот, тыс. руб.		Изменение средних цен во II квартале по сравнению с I кварталом, %
	I квартал	II квартал
Обувь	60	80	+12
Трикотаж	24	30	+5
Изделия из кожи	32	45	+2

Определить:

1) изменение цен на проданные товары (индекс цен);

2) общий индекс товарооборота;

3) общий индекс физического товарооборота.

Решение

1 Общий индекс цен вычислим в форме среднего гармонического индекса

,

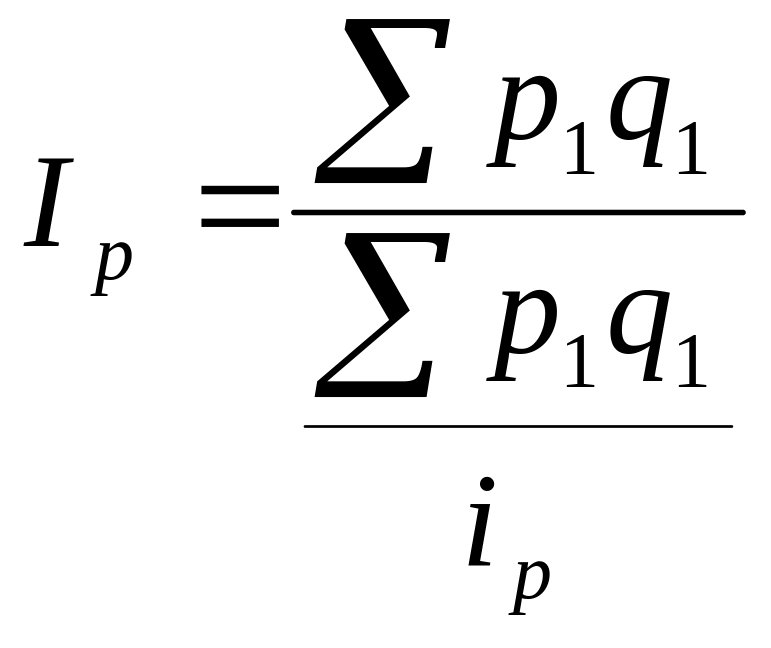где – индивидуальный индекс цен.

Определим индивидуальные индексы цен:

обувь 100 + 12 = 112%

трикотаж 100 + 5 = 105%

изделия из кожи 100 + 2 = 102%

Таким образом: 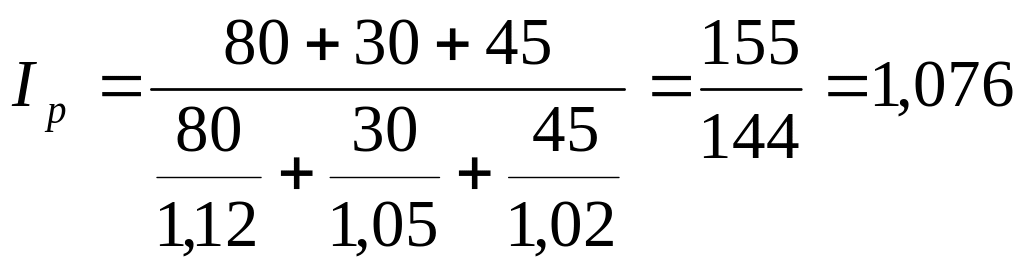или 107,6%, т. е. цены в среднем выросли на 7,6%.

Сумма перерасхода, полученная населением от повышения цен, составит

155 – 144 = + 11 тыс. руб.

2 Общий индекс товарооборота составит

или 133,6%, т. е. товарооборот во II квартале вырос по сравнению с I кварталом на 33,6%, а в денежном выражении – на 39 тыс. руб. (155 – 116).

3 Общий индекс физического объема товарооборота составит

или 124,1%, т. е. количество проданных товаров выросло на 24,1%, что составляет 28 тыс. руб.

Между вычисленными индексами существует взаимосвязь:

тыс. руб.

Пример 31

Имеются данные по одной из кондитерских фабрик (таблица 31.1).

Таблица 31.1 – Затраты на производство продукции кондитерской фабрики

Вид продукции	Общие затраты на производство продукции, тыс. ден. ед.		Индивидуальный индекс физического объема продукции
	базисный период	отчетный период
Карамель	25,0	27,0	1,05
Шоколадные конфеты	54,0	55,0	1,12

Определить абсолютное изменение затрат на производство продукции за счет изменения физического объема и себестоимости произведенной продукции.

Решение

Абсолютное изменение затрат на производство за счет изменения физического объема продукции ( ) найдем как разницу между числителем и знаменателем индекса физического объема

.

Из формулы выразим , тогда

или 109,8%,

тыс. ден. ед.

Абсолютное изменение затрат на производство за счет изменения себестоимости ( ) найдем как разницу между числителем и знаменателем сводного индекса себестоимости

или 94,5%,

тыс. ден. ед.

Следовательно, за счет роста объема произведенной продукции на 9,8% затраты на производство продукции выросли на 7,73 тыс. ден. ед., однако снижение цен на 5,5% способствовало снижению затрат на 4,73 тыс. ден. ед.

Пример 32

Имеются данные о производстве продукции и затратах времени на ее производство (таблица 32.1).

Таблица 32.1 – Объем производства продукции за базисный и отчетный год и затраты времени на ее производство

Вид продукции	Базисный год		Отчетный год
	произведено, тыс. ц ( )	затрачено тыс. чел./дн. ( )	произведено, тыс. ц ( )	затрачено тыс. чел./дн. ( )
Лук	45	7,3	48	7,5
Морковь	30	7,6	32	7,7

Определить индекс производительности труда.

Решение

Индекс производительности труда рассчитывается по формуле

,

где – индекс трудоемкости;

, – трудоемкость соответственно в базисном и отчетном году.

Трудоемкость рассчитывается по формуле

,

где – затраты рабочего времени;

– объем производства продукции.

Трудоемкость за отчетный период равна

чел.-дн./ц; чел.-дн./ц.

Трудоемкость за базисный период равна

чел.-дн./ц; чел.-дн./ц.

Таким образом

или 104,4%, т. е. производительность труда в отчетном периоде по сравнению с базисным увеличилась на 4,4%.

Пример 33

Динамика себестоимости и объема продукции характеризуется данными, представленными в таблице 33.1.

Таблица 33.1 – Объем произведенной продукции по заводам за базисный и отчетный периоды

Завод	Выработано продукции, тыс. ед.		Себестоимость единицы продукции, тыс. руб.
	базисный период ( )	отчетный период ( )	базисный период ( )	отчетный период ( )
Завод №1	7,0	7,4	150	180
Завод №2	6,8	7,0	140	150

Определить:

1) индекс себестоимости переменного состава;

2) индекс себестоимости постоянного состава;

3) индекс изменения структуры.

Решение

1 Индекс себестоимости переменного состава (индекс среднего уровня) рассчитывается по формуле

.

Индекс показывает, как изменилось среднее значение показателя за счет двух факторов (изменения самой себестоимости на отдельном заводе и изменений в структуре выработанной продукции).

или 116%.

2 Индекс себестоимости постоянного (фиксированного) состава рассчитывается по формуле

.

Индекс показывает, как изменилось среднее значение показателя за счет изменения первого фактора (себестоимости).

или 114%.

3 Индекс структурных сдвигов рассчитывается по формуле

.

Индекс показывает, как изменилось среднее значение показателя за счет изменения второго фактора (объема произведенной продукции).

или 102%.

Между этими индексами существует связь:

Следовательно, среднее значение себестоимости по двум заводам в отчетном периоде по сравнению с базисным увеличилось на 16%. За счет изменения себестоимости единицы продукции по отдельным заводам среднее значение себестоимости по двум заводам увеличилось на 14%. За счет изменений в структуре объема выработанной продукции среднее значение себестоимости увеличилось на 2%.

Пример 34

Расходы консолидированного бюджета Республики Беларусь на социально-культурные мероприятия представлены в таблице 34.1.

Таблица 34.1 – Расходы консолидированного бюджета Республики Беларусь на социально-культурные мероприятия

Виды расходов	Фактически действовавшая цена, млрд руб.		Объем расходов, млн руб.
	город А	город Б	город А	город Б
Здравоохранение	2964	3528	32,5	17,8
Образование	4060	4788	44,6	24,1
Физическая культура, спорт, культура и СМИ	695	919	7,6	4,6

Рассчитать территориальный индекс цен на эти виды расходов в городе А по сравнению с городом Б.

Решение

Территориальный индекс цен, в котором в качестве базы сравнений принимаются данные по городу А ( ), будет иметь вид

,

где , – фактически действующие цены в городе А и Б;

– количество расходов в городе А и Б.

Суммируем объем расходов в разных городах по каждому виду:

;

;

.

Рассчитаем территориальный индекс цен:

или 84,3%.

Таким образом, цены на расходы в городе А ниже на 15,7% по сравнению с ценами в городе Б.