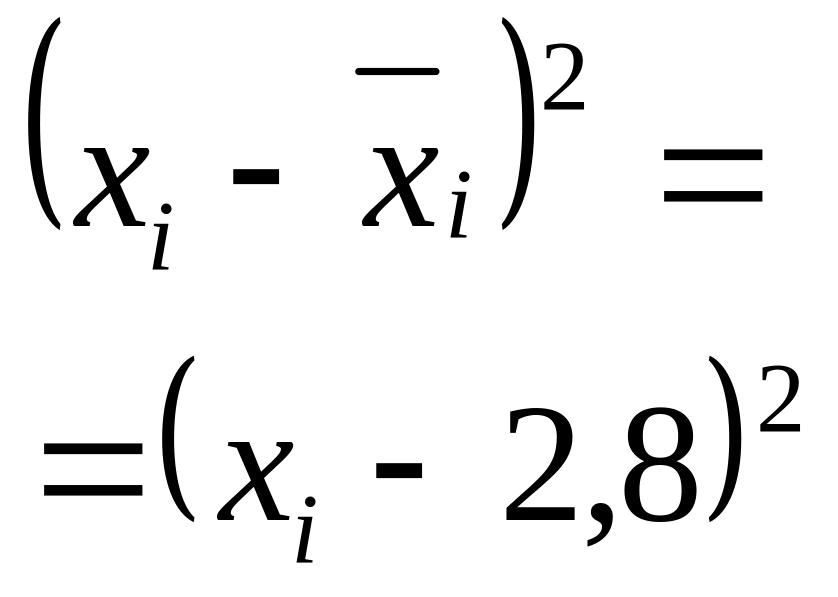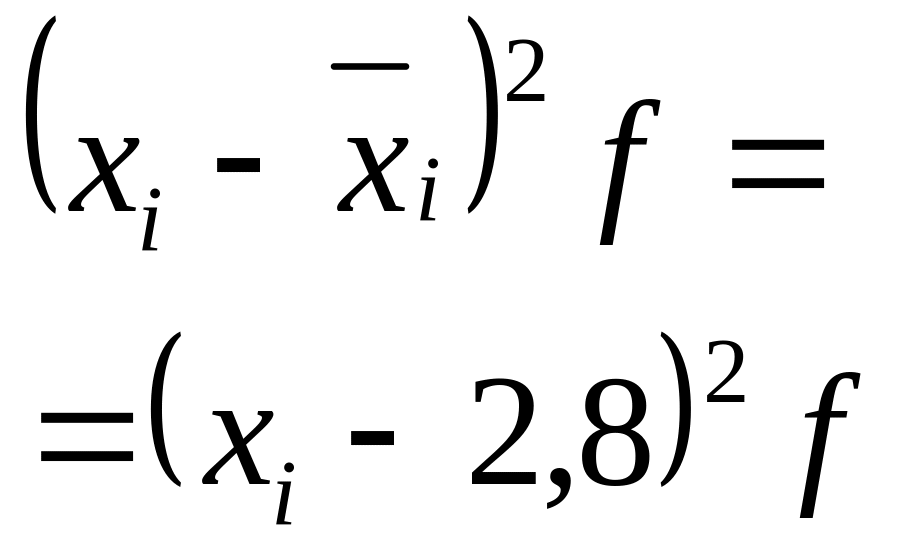- •Статистика
- •Часть I Теория статистики
- •Тема 1. Сводка и группировка статистических материалов
- •Тема 2. Абсолютные и относительные статистические
- •Тема 3. Средние величины
- •Тема 4. Показатели вариации
- •Тема 5. Индексы
- •Тема 6. Статистическое изучение динамики
- •Тема 7. Выборочное наблюдение
- •Тема 8. Статистическое изучение взаимосвязи
- •Статистика
- •Часть I Теория статистики
- •212027, Могилев, пр-т Шмидта, 3.
- •Рецензия
- •Министерство образования Республики Беларусь
- •Кафедра бухгалтерского учета, анализа и аудита выписка из протокола
Тема 4. Показатели вариации
Пример 21
Имеются данные о распределении рабочих по тарифным разрядам (таблица 21.1).
Таблица 21.1 – Распределение рабочих по тарифным разрядам
Тарифный разряд |
2 |
3 |
4 |
5 |
6 |
Число рабочих |
1 |
2 |
6 |
8 |
3 |
Определить: а) дисперсию; б) среднее квадратическое отклонение; в) коэффициент вариации.
Решение
Дисперсия
(![]() ),
или средний квадрат отклонений для
рядов распределения, исчисляется по
формуле
),
или средний квадрат отклонений для
рядов распределения, исчисляется по
формуле
![]() ,
,
т. е. является средней арифметической квадратов отклонений каждого значения признака от общей средней.
Корень квадратный из дисперсии называется средним квадратическим отклонением:
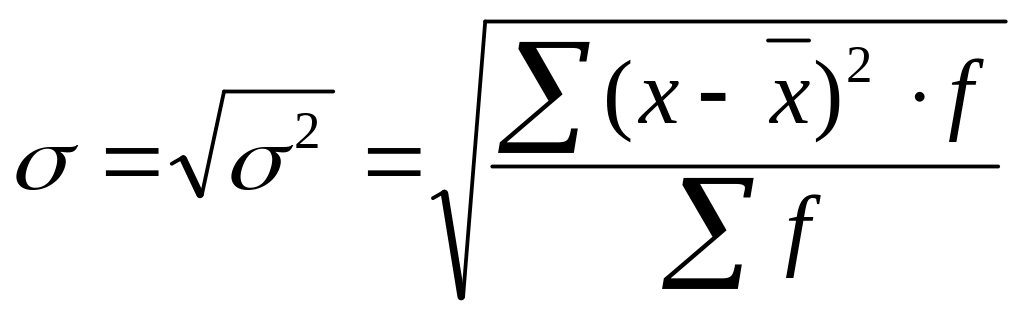 .
.
Выражается он в единицах измерения изучаемого признака.
Коэффициент вариации – относительный показатель колеблемости, равный процентному отношению среднего квадратического отклонения к средней арифметической:
![]() .
.
Как величина относительная, выраженная в процентах, коэффициент вариации применяется для сравнения степени вариации различных признаков.
Как видно из формул, для расчета показателей вариации необходимо предварительно определить среднюю величину. Исчислим указанные выше показатели вариации, представив необходимые расчеты в таблице 21.2.
Таблица 21.2 – Расчет показателей вариации
Тарифный разряд, |
Число рабочих, чел., |
|
|
|
|
2 |
1 |
2 |
- 2,5 |
- 2,5 |
6,25 |
3 |
2 |
6 |
- 1,5 |
- 3,0 |
4,50 |
4 |
6 |
24 |
- 0,5 |
3,0 |
1,50 |
5 |
8 |
40 |
0,5 |
4,0 |
2,00 |
6 |
3 |
18 |
1,5 |
4,5 |
6,75 |
Итого |
20 |
90 |
- |
- |
21,00 |
Определим показатели:
![]() разряда.
разряда.
![]() .
.
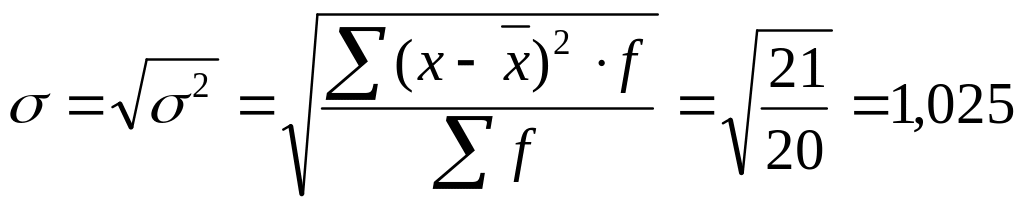 разряда.
разряда.
![]() .
.
Так
как
![]() <
40%, то совокупность достаточно однародна
и средняя характеристика достаточна
надежна.
<
40%, то совокупность достаточно однародна
и средняя характеристика достаточна
надежна.
Пример 22
По данным условия предыдущего примера исчислить дисперсию по формуле
![]() .
.
Решение
Все расчеты представим в таблице 22.1.
Таблица 22.1 – Расчет дисперсии
Тарифный разряд, |
Число рабочих, чел., |
|
|
|
2 |
1 |
2 |
4 |
4 |
3 |
2 |
6 |
9 |
18 |
4 |
6 |
24 |
16 |
96 |
5 |
8 |
40 |
25 |
200 |
6 |
3 |
18 |
36 |
108 |
Итого |
20 |
90 |
- |
426 |
Дисперсия равна

![]() .
.
Среднее квадратическое отклонение:
![]() разряда.
разряда.
Пример 23
Имеются данные о распределении работников организации обслуживания населения по размеру средней месячной заработной платы (таблица 23.1).
Таблица 23.1 – Распределение работников организации обслуживания населения по размеру средней месячной заработной платы
Группы работников по размеру заработной платы, руб. |
Численность работников, чел. |
До 100 |
2 |
100-120 |
12 |
120-140 |
15 |
140-160 |
64 |
160-180 |
55 |
180-200 |
32 |
Свыше 200 |
20 |
Итого |
200 |
Определить дисперсию заработной платы по способу моментов.
Решение
Способ моментов основан на математических свойствах дисперсии, применение которых значительно упрощает технику ее вычисления, а для рядов распределения с равными интервала приводит к формуле
![]() ,
,
где – длина интервала;
 – момент
первого порядка;
– момент
первого порядка;
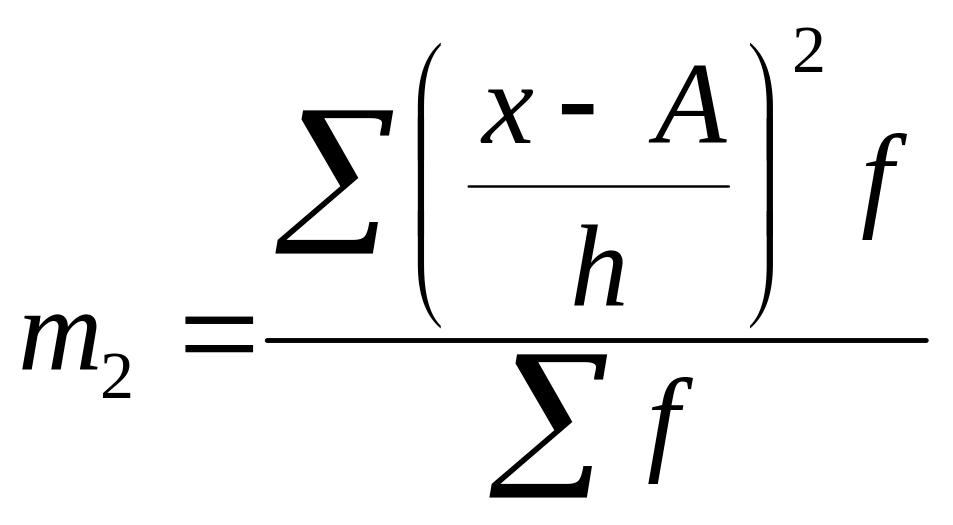 – момент
второго порядка;
– момент
второго порядка;
– ложный ноль.
Определим дисперсию по формуле, представив необходимые расчеты в таблице 23.2.
Таблица 23.2 – Расчет дисперсии способом моментов
Группы работников по размеру заработной платы, руб., |
Число работников, чел., |
Середина интервала, |
|
|
|
До 100 |
2 |
90 |
-3 |
-6 |
18 |
100-120 |
12 |
110 |
-2 |
-24 |
48 |
120-140 |
15 |
130 |
-1 |
-15 |
15 |
140-160 |
64 |
150 |
0 |
0 |
0 |
160-180 |
55 |
170 |
1 |
55 |
55 |
180-200 |
32 |
190 |
2 |
64 |
128 |
Свыше 200 |
20 |
210 |
3 |
60 |
180 |
Итого |
200 |
- |
- |
134 |
444 |
Исчислим моменты первого и второго порядка:
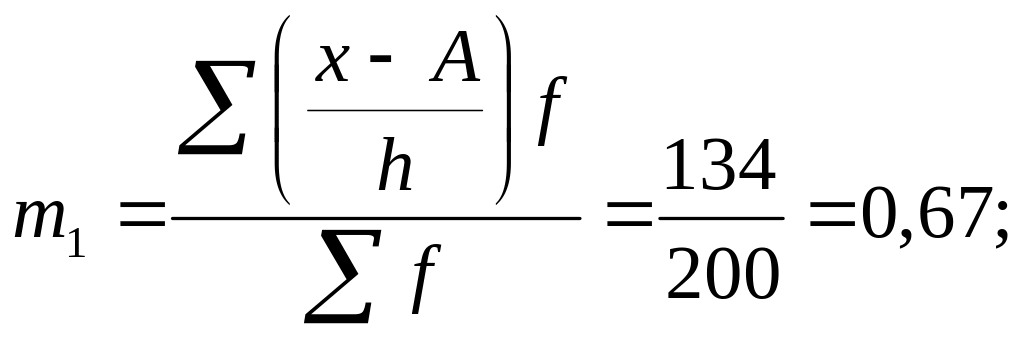
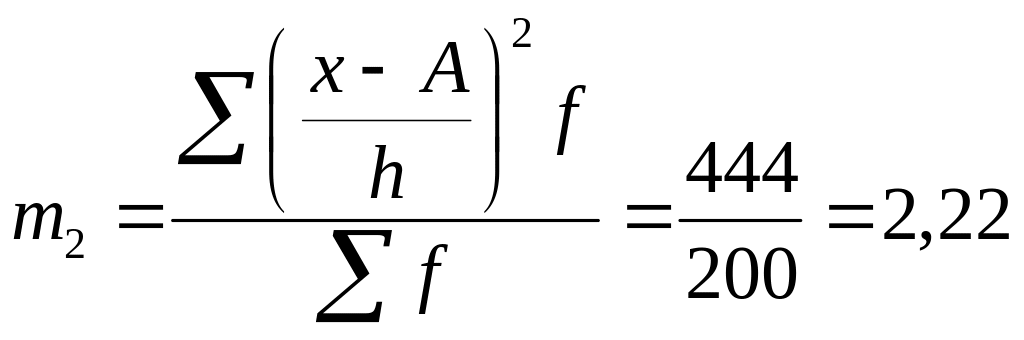 .
.
Затем вычислим средний квадрат отклонений (дисперсию):
![]() .
.
Пример 24
Удельный вес основных рабочих в трех цехах предприятия составил: 80, 75 и 90% общей численности рабочих. Определить дисперсию и среднее квадратическое отклонение доли основных рабочих по предприятию в целом, если численность всех рабочих трех цехов составила соответственно 100, 200 и 150 человек.
Решение
Рабочие предприятия подразделяются на две группы: основные и ремонтно-вспомогательные рабочие.
Общая численность основных рабочих по предприятию в целом составит:
![]() человек.
человек.
Доля основных рабочих по предприятию
![]() .
.
Дисперсия альтернативного признака составит
![]() ,
,
где
![]() – доля единиц, обладающих данным
признаком (доля основных рабочих);
– доля единиц, обладающих данным
признаком (доля основных рабочих);
![]() – доля
единиц, не обладающих данным признаком
(доля ремонтно-вспомогательных рабочих).
– доля
единиц, не обладающих данным признаком
(доля ремонтно-вспомогательных рабочих).
Поскольку
![]() ,
следовательно,
,
следовательно,
![]() и формула дисперсии имеет вид
и формула дисперсии имеет вид
![]() .
.
Среднее квадратическое отклонение доли основных рабочих по предприятию в целом:
![]() .
.
Пример 25
Для изучения взаимосвязи между стажем работы и производительностью труда (часовой выработкой) произведена группировка рабочих, приведенная в таблице 25.1.
Таблица 25.1 – Группировка рабочих по стажу работы с указанием среднечасовой выработки продукции на одного рабочего
Группа, № |
Группы рабочих по стажу, лет |
Число рабочих, чел. |
Среднечасовая выработка продукции одного рабочего, шт. |
I |
До 3 |
5 |
2; 2; 3; 3; 4 |
II |
3 – 5 |
15 |
2; 2; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 4; 4; |
Определить:
1) среднюю часовую выработку продукции по каждой группе рабочих и по двум группам вместе;
2) дисперсию по каждой группе рабочих (групповые дисперсии) и среднюю из групповых дисперсий;
3) дисперсию групповых средних от общей средней (межгрупповую дисперсию);
4) общую дисперсию по правилу вложения дисперсий;
5) коэффициент детерминации;
6) эмпирическое корреляционное отношение.
Решение
1 Определим среднюю выработку по каждой группе рабочих и по двум группам:
![]() шт.;
шт.;
![]() шт.;
шт.;
![]() шт.
или
шт.
или
![]() шт.
шт.
2 Исчислим дисперсии по каждой группе рабочих по формуле:
![]() .
.
Предварительно строим по каждой группе рабочих ряды распределения по выработке (таблицы 25.2 и 25.3). Затем исчислим групповые дисперсии.
Таблица 25.2 – Ряд распределения первой группы рабочих по выработке
Выработка, шт., |
Число рабочих, чел., |
|
|
|
2 |
2 |
- 0,8 |
0,64 |
1,28 |
3 |
2 |
0,2 |
0,04 |
0,08 |
4 |
1 |
1,2 |
1,44 |
1,44 |
Итого |
5 |
- |
- |
2,80 |
Дисперсия
для первой группы
![]() .
.
Таблица 25.3 – Ряд распределения второй группы рабочих по выработке
Выработка, шт., |
Число рабочих, чел., |
|
|
|
2 |
2 |
- 1,4 |
1,96 |
3,92 |
3 |
5 |
- 0,4 |
0,16 |
0,80 |
4 |
8 |
0,6 |
0,36 |
2,88 |
Итого |
15 |
- |
- |
7,60 |
Дисперсия
для второй группы
![]() .
.
Исчислим среднюю из групповых (частных) дисперсий по формуле
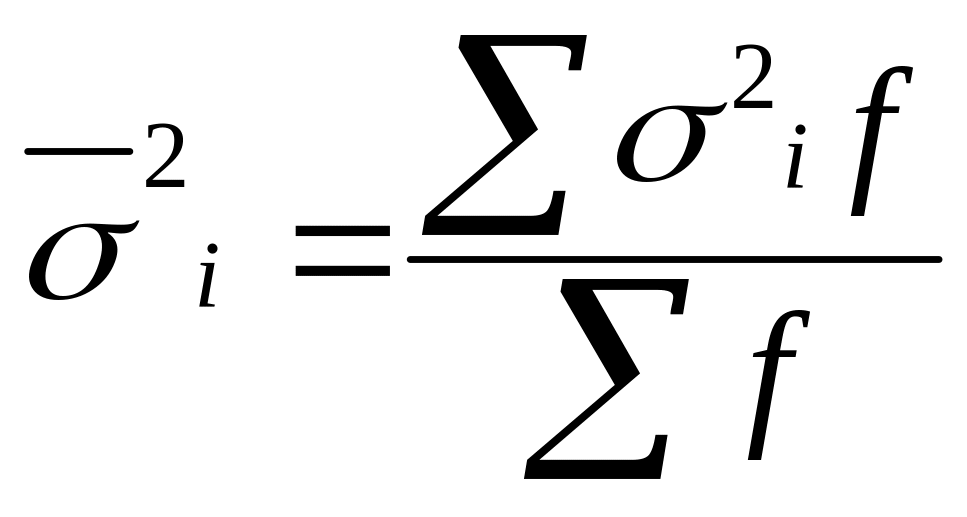 ;
;
![]() .
.
3 Межгрупповая дисперсия
![]() ;
;
![]() .
.
4 Определим общую дисперсию по правилу сложения дисперсий
![]() ;
;
![]() .
.
5 Определяем коэффициент детерминации
![]() или
11,5%.
или
11,5%.
Коэффициент детерминации показывает, что вариация среднечасовой выработки рабочих обусловлена вариацией стажа лишь на 11,5%.
6 Исчислим эмпирическое корреляционное отношение
![]() .
.
Оно показывает, что для данной группы рабочих связь между производственным стажем и среднечасовой выработкой незначительная.
Пример 26
Имеются данные о времени простоя автомобиля под разгрузкой (таблица 26.1).
Таблица 26.1 – Время простоя автомобиля под разгрузкой
№ пункта разгрузки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Число грузчиков |
3 |
4 |
4 |
3 |
3 |
4 |
4 |
4 |
3 |
4 |
Время простоя, мин. |
12 |
10 |
8 |
15 |
19 |
12 |
8 |
10 |
18 |
8 |
Проверить закон сложения дисперсий.
Решение
В данной задаче варьирующим признаком является время простоя автомобиля под разгрузкой. Общая дисперсия времени простоя под разгрузкой определяется по формуле
![]() .
.
Для расчета общей дисперсии составляется дискретный ряд распределения, промежуточные расчеты представим в таблице 26.2.
Таблица 26.2 – Вспомогательная таблица для расчета общей дисперсии
Время простоя под разгрузкой, мин, |
Число выполненных разгрузок, |
|
|
|
|
8 |
3 |
24 |
- 4 |
16 |
48 |
10 |
2 |
20 |
- 2 |
4 |
8 |
12 |
2 |
24 |
0 |
0 |
0 |
15 |
1 |
15 |
3 |
9 |
9 |
18 |
1 |
18 |
6 |
36 |
36 |
19 |
1 |
19 |
7 |
49 |
49 |
Итого |
10 |
120 |
- |
- |
150 |
![]() мин
– среднее время простоя.
мин
– среднее время простоя.
![]() – общая
дисперсия.
– общая
дисперсия.
Величина этой дисперсии характеризует вариацию времени простоя под разгрузкой под влиянием всех условий.
Различия в величине изучаемого признака прежде всего возникают под влиянием числа грузчиков, принимающих участие в процессе разгрузки. В связи с этим в совокупности выделяются две однородные группы по числу грузчиков: в первую группу включаются наблюдения при числе грузчиков 3; во вторую группу попадают наблюдения при числе грузчиков 4. Для каждой из выделенных групп определяется внутригрупповая дисперсия, возникающая под влиянием неучтенных факторов. Для их расчета использованы вспомогательные таблицы 26.3 и 26.4.
Таблица 26.3 – Расчет внутригрупповой дисперсии по первой группе (число грузчиков, участвующих в разгрузке, – 3)
Время простоя под разгрузкой, мин, |
Число выполненных разгрузок, |
|
|
|
12 |
1 |
12 |
- 4 |
16 |
15 |
1 |
15 |
- 1 |
1 |
18 |
1 |
18 |
2 |
4 |
19 |
1 |
19 |
3 |
9 |
Итого |
4 |
64 |
- |
30 |
![]() мин.;
мин.;
![]() .
.
Таблица 26.4 – Расчет внутригрупповой дисперсии по второй группе (число грузчиков, участвующих в разгрузке, – 4)
Время простоя под разгрузкой, мин, |
Число выполненных разгрузок, |
|
|
|
8 |
3 |
24 |
- 1,33 |
5,31 |
10 |
2 |
20 |
0,67 |
0,90 |
12 |
1 |
12 |
2,67 |
7,13 |
Итого |
6 |
56 |
- |
13,37 |
![]() мин.;
мин.;
![]() .
.
Средняя из групповых дисперсий

Межгрупповая дисперсия, отражающая различия в величине признака под влиянием фактора, положенного в основу группировки, определяется по формуле
![]()
Общая
дисперсия (![]() )
равна сумме средней внутригрупповой
дисперсии и межгрупповой дисперсии
)
равна сумме средней внутригрупповой
дисперсии и межгрупповой дисперсии
![]() ,
,
что и соответствует полученной ранее величине.
Пример 27
Имеются данные о результатах обследования рабочих предприятия по размеру месячной заработной платы (таблица 27.1).
Таблица 27.1 – Информация о численности рабочих по возрасту и размере заработной платы
Группы рабочих по возрасту, лет |
Число рабочих |
Дисперсия заработной платы |
До 20 |
100 |
300 |
20-30 |
120 |
400 |
30 и старше |
150 |
500 |
Общая дисперсия заработной платы в обследованной совокупности рабочих составила 450.
Определить, в какой степени вариация заработной платы рабочих предприятия зависит от возраста.
Решение
Средняя внутригрупповая дисперсия характеризует случайную вариацию под влиянием неучтенных факторов
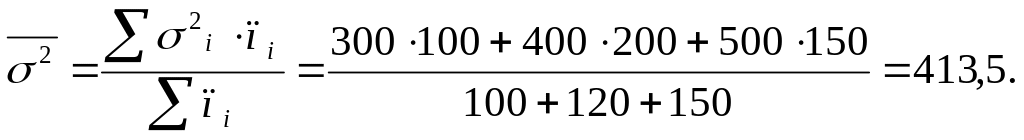
Межгрупповая дисперсия отражает систематическую вариацию под влиянием фактора, положенного в основу группировки (возраста рабочих).
Межгрупповая дисперсия определяется по правилу сложения дисперсий
![]()
Отсюда соотношение дисперсий
![]() или
8,0%.
или
8,0%.
Полученный результат показывает, что возраст на варьирование заработной платы рабочих предприятия не оказывает существенного влияния.
Пример 28
Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250. Найти среднюю величину.
Решение
Для нахождения средней величины воспользуемся формулой
![]() ,
,
где
![]() – средняя арифметическая из квадратов
индивидуальных значений признака;
– средняя арифметическая из квадратов
индивидуальных значений признака;
![]() – квадрат
среднего значения признака.
– квадрат
среднего значения признака.
Тогда
![]() .
.
Средняя величина признака
![]() .
.