Тема 3. Средние величины
Пример 15
Данные о заработной плате бригады рабочих приведены в таблице 15.1.
Таблица 15.1 – Заработная плата бригады рабочих по отдельным профессиям за месяц
Шлифовщик |
Слесарь |
Токарь |
|||
заработная плата, ден. ед. |
число рабочих, чел. |
заработная плата, ден. ед. |
число рабочих, чел. |
заработная плата, ден. ед. |
число рабочих, чел. |
200 |
1 |
220 |
2 |
230 |
3 |
210 |
1 |
236 |
2 |
242 |
5 |
217 |
1 |
240 |
2 |
255 |
2 |
Итого |
3 |
- |
6 |
- |
10 |
Определить среднюю заработную плату рабочих по каждой профессии и в целом по бригаде.
Решение
Число рабочих известно. Исчислим фонд заработной платы шлифовщиков путем суммирования заработка каждого рабочего. В данном случае веса (частоты) равны единице. Следовательно, расчет средней заработной платы рабочих производится по формуле средней арифметической простой:
ден.
ед.,
где
– варианта (значение признака);
– количество вариант.
Если веса (частоты) в рядах распределения равны между собой, как это имеет место в бригаде слесарей, расчет средней производится по формуле средней арифметической простой. Следовательно, средняя заработная плата слесарей будет равна:
ден.
ед.
Если частоты имеют различные количественные значения, как в группе токарей, то средняя заработная плата определяется по формуле средней арифметической взвешенной:
ден.
ед.
где – варианта (значение признака);
– частота,
с которой варианта встречается в
совокупности.
В этом примере фонд заработной платы равен сумме произведений заработной платы каждого рабочего на их число.
Средняя заработная плата бригады рабочих в целом может быть определена двумя способами:
а) отношением фонда заработной платы рабочих по группам профессий к общей численности рабочих этих групп:
ден.
ед.
б) как средняя арифметическая взвешенная из групповых средних:
ден.
ед.
Пример 16
По данным обследования получены данные о распределении студентов-заочников по возрасту (таблица 16.1).
Таблица 16.1 – Распределение студентов-заочников по возрасту
Группа, № п/п |
Группы студентов по возрасту, лет, |
Число студентов, чел., |
Удельный вес студентов в группе |
|
в
%,
|
в
коэффициентах,
|
|||
1 |
2 |
3 |
4 |
5 |
1 |
20-25 |
200 |
10 |
0,10 |
2 |
25-30 |
900 |
45 |
0,45 |
3 |
30-35 |
800 |
40 |
0,40 |
4 |
35-40 |
100 |
5 |
0,05 |
Итого |
2000 |
100 |
1,00 |
|
Определить средний возраст студентов-заочников, используя в качестве веса:
1) число студентов;
2) удельный вес студентов в группе.
Решение
Среднее
значение признака по данным вариационного
ряда распределения определяется по
средней арифметической взвешенной:
.
Чтобы
применить эту формулу, надо значения
признака в интервале (варианты) выразить
одним числом, т. е. дискретной величиной,
за которую принимается середина интервала
каждой группы. Так, варианта первой
группы
и т. д. по остальным группам. Расчеты
удобнее располагать в таблице 16.2.
Таблица 16.2 – Распределение студентов-заочников по возрасту
Группы студентов по возрасту, лет, |
Число студентов, чел., |
Середина интервала, |
|
|
|
25-25 |
200 |
22,5 |
4500 |
225 |
2,25 |
25-30 |
900 |
27,5 |
24750 |
1237,5 |
12,375 |
30-35 |
800 |
32,5 |
26000 |
1300 |
13,00 |
35-40 |
100 |
37,5 |
3750 |
187,5 |
1,875 |
Итого |
2000 |
- |
59000 |
2950,0 |
29,5 |
Таким
образом,
года.
Аналогично производятся расчеты, если в качестве весов (частот) взяты относительные величины, которые могут быть выражены в процентах или коэффициентах. Следовательно, средний возраст студентов-заочников, исчисленный по относительным величинам, будет равен:
а) если весами являются проценты:
года;
б) если весами являются коэффициенты:
года.
Получен тот же результат.
В рядах распределения с открытыми интервалами величина интервала условно принимается равной интервалу соседних групп. Если, например, первая группа студентов имеет возраст до 25 лет, а четвертая – свыше 35 лет, то интервал первой группы приравнивается к интервалу следующей за ней второй группы, а четвертой – величине интервала предшествующей третьей группы. Дальнейший расчет аналогичен изложенному выше.
Пример 17
Распределение промышленных предприятий отрасли по численности работающих приведено в таблице 17.1.
Таблица 17.1 – Распределение промышленных предприятий отрасли по численности работающих
Группы предприятий по числу работающих, чел. |
Число предприятий |
До 5000 |
20 |
5000-6000 |
40 |
6000-7000 |
80 |
7000-8000 |
50 |
Свыше 8000 |
10 |
Итого |
200 |
Определить среднюю численность работающих на предприятиях отрасли, применяя способ моментов.
Решение
1
Перейдем от интервального ряда к
дискретному, приняв в качестве варианты
середину интервала, т. е. полусумму
верхней и нижней границы интервала,
например,
и т. д.
Так
как ряд имеет открытые интервалы, то
недостающие границы надо определить
условно, при этом принято считать, что
первый интервал имеет такую же длину
как последующий, а последующий – как
предыдущий. Так как длины всех интервалов
равны 1000, то для первого интервала
недостающая граница равна 4000 (5000 – 1000)
и середина
.
Для последнего интервала недостающая
граница равна 9000 (8000 + 1000), а середина
интервала –
.
Так как мы имеем ряд с равными интервалами, то можно было найти середину только первого интервала, а каждая последующая середина будет отличаться от предыдущей на длину интервала (на 1000).
Расчеты сведем в таблицу 17.2.
Таблица 17.2 – Расчетная таблица
Группы предприятий по числу работающих, чел., |
Число предприятий, |
Середина интервала, |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
До 5000 |
20 |
4500 |
- 2 |
10 |
- 20 |
5000-6000 |
40 |
5500 |
- 1 |
20 |
- 20 |
6000-7000 |
80 |
6500 |
0 |
40 |
0 |
7000-8000 |
50 |
7500 |
1 |
25 |
25 |
Свыше 8000 |
10 |
8500 |
2 |
5 |
10 |
Итого |
200 |
- |
- |
100 |
- 5 |
,
%
2
Определим так называемый «ложный ноль»
– это варианта стоящая в середине
вариационного ряда и имеющая наибольшую
частоту. Для нашего примера такой
вариантой будет
,
т. к. ей соответствует частота
.
3 Определим условные варианты по формуле:
,
где – ложный ноль;
– длина
интервала.
Результаты вычисления приведены в гр. 4 таблицы 17.2.
4 Так как частоты большие числа, переведем их в проценты по формуле:
.
Для
нашего примера
(см. гр. 5 таблицы 17.2).
5
Вычислим
(гр. 6 таблицы 17.2).
6 Определим момент первого порядка по формуле:
.
7 Определим среднее значение признака, применяя способ моментов:
чел.
Вывод: Средняя численность работающих на предприятиях отрасли составляет 6450 чел.
Пример 18
Средняя выработка продукции на одного рабочего за смену в двух цехах завода, вырабатывающих однородную продукцию, характеризуется данными, представленными в таблице 18.1.
Таблица 18.1 – Выработка продукции по цехам завода
Бригада, № |
Цех №1 |
Бригада, № |
Цех №2 |
||
дневная выработка продукции, шт., |
число рабочих, чел., |
дневная выработка продукции, шт., |
объем
произведенной продукции, шт.,
|
||
I |
20 |
8 |
IV |
38 |
418 |
II |
30 |
11 |
V |
36 |
432 |
III |
35 |
16 |
VI |
20 |
140 |
Определить среднедневную выработку продукции рабочих:
а) по первому цеху; б) по второму цеху.
Решение
Основой расчета является экономическое содержание показателя:
Среднедневная
выработка рабочего =
.
По первому цеху расчет произведем по средней арифметической взвешенной, т. к. неизвестен числитель отношения:
шт.
По второму цеху – по средней гармонической взвешенной, т. к. неизвестен знаменатель отношения:
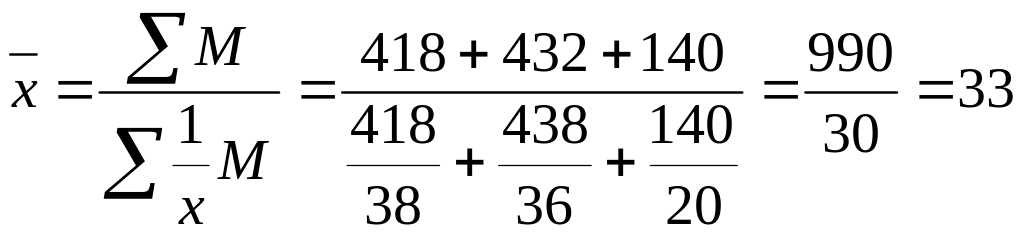шт.
Пример 19
Имеются данные о распределении рабочих по тарифному разряду (таблица 19.1).
Таблица 19.1 – Распределение рабочих по тарифному разряду
Тарифный разряд, |
Число рабочих, в % к итогу, |
Сумма накопленных частот,
|
1 |
1 |
1 |
2 |
3 |
4 |
3 |
10 |
14 |
4 |
49 |
63 |
5 |
28 |
|
6 |
9 |
|
Итого |
100 |
|
Определить моду и медиану.
Решение
В
дискретных рядах модой (
)
является варианта с наибольшей частотой.
В примере наибольшее число рабочих
имеют четвертый разряд (49%). Следовательно,
мода равна четвертому разряду. Для
вычисления медианы (
)
надо определить сумму накопленных
частот ряда, составляющую половину
общей суммы частот. Общая сумма частот
для данного примера равна 100, а половина
– 50. Чтобы найти накопленную частоту,
надо к каждой частоте прибавить предыдущую
сумму. В графе 3 накопленная сумма частот
составляет 63. Варианта
,
соответствующая этой сумме, т. е.
четвертому разряду, есть медиана.
Вывод:
Наибольшее число рабочих имеют тарифный
разряд равный 4 (т.к.
).
Половина рабочих имеет тарифный разряд
менее 4, а вторая половина – более 4 (т.к.
).
Пример 20
Имеются данные о распределении рабочих по затратам времени на обработку одной детали (таблица 20.1).
Таблица 20.1 – Распределение рабочих по затратам времени на обработку одной детали
Затраты времени на одну деталь, мин., |
Число рабочих, чел., |
Сумма накопленных частот, |
4,5-5,5 |
8 |
8 |
5,5-6,5 |
18 |
26 |
6,5-7,5 |
23 |
49 |
7,5-8,5 |
30 |
79 |
8,5-9,5 |
12 |
|
9,5-10,5 |
6 |
|
10,5-11,5 |
3 |
|
Итого |
100 |
|
Определить моду и медиану.
Решение
В интервальных рядах распределения с равными интервалами мода ( ) и медиана ( ) определяются по формулам:
,
где
– начальное значение модального
интервала;
– длина
модального интервала;
– частота
модального интервала;
– частота
интервала, предшествующего модальному;
– частота
интервала, следующего за модальным.
Следовательно,
мин, т. е. наибольшее число рабочих
затрачивает на обработку одной детали
около 8 мин.
,
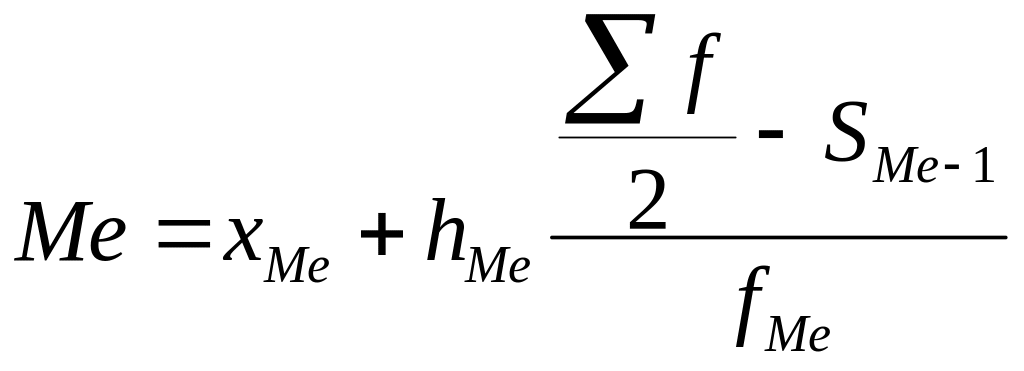где
– начальное значение медианного
интервала;
– длина
медианного интервала;
– сумма
частот ряда;
– сумма
накопленных частот интервала,
предшествующего медианному;
– частота
медианного интервала.
Следовательно,
мин, т. е. одна половина рабочих затрачивает
на обработку детали до 7,53 мин, другая –
свыше 7,53 мин.