Министерство образования Республики Беларусь
Учреждение образования
«Могилевский государственный университет
продовольствия»
Кафедра бухгалтерского учета, анализа и аудита
Статистика
Часть I Теория статистики
Методические указания к решению задач
для студентов экономических специальностей
Могилев 2010
УДК 311.1
Рассмотрены и рекомендованы к изданию на заседании кафедры бухгалтерского учета, анализа и аудита
Протокол № 4 от 19.11.2009 г.
УМС по специальностям 1 – 25 01 08 и 1 – 25 01 04
Протокол № 3 от 19.11.2009 г.
Составители:
старший преподаватель О.Д. Малышева,
ассистент О.Г. Барсукова,
ассистент О.К. Шкинёва
Рецензент
к.э.н., доцент Т.И. Сушко
УДК 311.1
© УО «Могилевский государственный университет продовольствия», 2010
Тема 1. Сводка и группировка статистических материалов
Пример 1
Имеются данные о рабочих-сдельщиках за месяц (таблица 1.1).
Таблица 1.1 – Данные о стаже работы рабочих-сдельщиков и выработке продукции за месяц
№ п/п |
Стаж работы, лет |
Выработка рабочего, ден.ед. |
№ п/п |
Стаж работы, лет |
Выработка рабочего, ден.ед. |
1 |
1,0 |
200 |
16 |
10,5 |
276 |
2 |
1,0 |
202 |
17 |
1,0 |
234 |
3 |
3,0 |
205 |
18 |
9,0 |
270 |
4 |
6,5 |
290 |
19 |
9,0 |
264 |
5 |
9,2 |
298 |
20 |
6,5 |
252 |
6 |
4,4 |
250 |
21 |
5,0 |
241 |
7 |
6,9 |
280 |
22 |
6,0 |
256 |
8 |
2,5 |
230 |
23 |
10,1 |
262 |
9 |
2,7 |
223 |
24 |
5,5 |
245 |
10 |
16,0 |
310 |
25 |
2,5 |
240 |
11 |
13,2 |
284 |
26 |
5,0 |
244 |
12 |
14,0 |
320 |
27 |
5,3 |
252 |
13 |
11,0 |
295 |
28 |
7,5 |
253 |
14 |
12,0 |
279 |
29 |
7,0 |
252 |
15 |
4,5 |
222 |
30 |
8,0 |
262 |
Для изучения зависимости между стажем работы и месячной выработкой рабочих произвести группировку рабочих по стажу, образовав 5 групп с равными интервалами. Каждую группу охарактеризовать: числом рабочих; средним стажем работы; месячной выработкой продукции – всего и в среднем на одного рабочего.
Результаты представить в таблице и сделать выводы.
Решение
Применяя метод группировок для взаимосвязи, необходимо, прежде всего, определить факторный признак, оказывающий влияние на взаимосвязанные с ним признаки. Таким признаком в нашем примере является стаж работы, который должен быть положен в основание группировки. По условию требуется выделить пять групп рабочих по стажу с равными интервалами.
Если интервалы равны, то величина интервала группировочного признака (стажа работы) определяем по формуле
,
где
,
– максимальное и минимальное значение
признака;
– число
образуемых групп.
Для
нашего примера величина интервала
равна:
года.
Следовательно, первая группа рабочих имеет стаж 1-4 года, вторая – 4-7 и т.д. Для построения и оформления результатов группировки составим рабочую таблицу 1.2.
Таблица 1.2 – Группировка рабочих по стажу работы
Группы рабочих по стажу, лет |
Номер рабочего |
Стаж, лет |
Месячная выработка, ден. ед. |
|
1 |
1-4 |
1 2 3 8 9 17 25 |
1,0 1,0 3,0 2,5 2,7 1,0 2,5 |
200 202 205 230 223 234 240 |
|
Итого |
7 |
13,7 |
1 534 |
2 |
4-7 |
6 4 15 20 21 22 24 26 27 7 |
4,4 6,5 4,5 6,5 5,0 6,0 5,5 5,0 5,3 6,9 |
250 290 222 252 241 256 245 244 252 280 |
|
Итого |
10 |
55,6 |
2 532 |
3 |
7-10 |
5 18 19 28 29 30 |
9,2 9,0 9,0 7,5 7,0 8,0 |
298 270 264 253 252 262 |
|
Итого |
6 |
49,7 |
1 599 |
4 |
10-13 |
13 14 16 23 |
11,0 12,0 10,5 10,1 |
295 279 276 262 |
|
Итого |
4 |
43,6 |
1 112 |
5 |
13-16 |
10 11 12 |
16,0 13,2 14,0 |
310 284 320 |
|
Итого |
3 |
43,2 |
914 |
|
Всего |
30 |
206 |
7 691 |
Групповые показатели рабочей таблицы и исчисленные на их основе средние показатели занесем в сводную аналитическую таблицу 1.3.
Таблица 1.3 – Сводная таблица группировки рабочих по стажу работы
Группы рабочих по стажу, лет |
Число рабочих, чел. |
Стаж, лет |
Месячная выработка, ден. ед. |
|||
всего |
в среднем по группе |
всего |
на одного работника |
|||
1 |
2 |
3 |
4=3/2 |
5 |
6=5/2 |
|
1 |
1-4 |
7 |
13,7 |
1,96 |
1534 |
219,1 |
2 |
4-7 |
10 |
55,6 |
5,56 |
2532 |
253,2 |
3 |
7-10 |
6 |
49,7 |
8,28 |
1599 |
266,5 |
4 |
10-13 |
4 |
43,6 |
10,9 |
1112 |
278,0 |
5 |
13-16 |
3 |
43,2 |
14,4 |
914 |
304,7 |
|
Итого |
30 |
205,8 |
6,86 |
7691 |
256,4 |
Сравнивая графы 5 и 7 таблицы 1.3, видно, что с увеличением стажа рабочих растет месячная выработка продукции. Следовательно, между изучаемыми признаками (показателями) имеется прямая зависимость.
Для полноты анализа сравним результативные показатели по каждой группе с показателями первой группы и представим результаты в таблице 1.4.
Таблица 1.4 – Зависимость выработки продукции от стажа рабочих
Группы рабочих по стажу, лет |
Число рабочих, чел. |
Месячная выработка продукции на одного рабочего, ден. ед. |
Прирост месячной выработки продукции на одного рабочего к 1 группе |
||
абсолютный, ден. ед. |
относительный, % |
||||
1 |
2 |
3 |
4 |
5 |
|
1 |
1-4 |
7 |
219,1 |
- |
- |
2 |
4-7 |
10 |
253,2 |
34,1 |
15,6 |
3 |
7-10 |
6 |
266,5 |
47,4 |
21,6 |
4 |
10-13 |
4 |
278,0 |
58,9 |
26,9 |
5 |
13-16 |
3 |
304,7 |
85,6 |
39,1 |
|
Итого |
30 |
- |
- |
- |
Данные таблицы 1.4 показывают тенденцию роста выработки продукции от стажа работы. С ростом стажа постепенно увеличивается прирост продукции. Рабочие пятой группы, наиболее квалифицированные и опытные произвели продукции на 85,6 ден. ед. или на 39,1% больше по сравнению с рабочими первой группы. Следовательно, подтверждается вывод, сделанный ранее, что между изучаемыми признаками имеется прямая связь.
Пример 2
Имеются следующие данные (таблица 2.1).
Таблица 2.1 – Распределение рабочих двух предприятий по проценту выполнения норм выработки
Предприятие №1 |
Предприятие №2 |
||
группа рабочих по проценту выполнения норм выработки, % |
количество рабочих, % к итогу |
группа рабочих по проценту выполнения норм выработки, % |
количество рабочих, % к итогу |
До 95 |
3 |
До 100 |
5 |
95-100 |
5 |
100-110 |
25 |
100-110 |
45 |
110-125 |
40 |
110-120 |
25 |
125-150 |
20 |
120-130 |
10 |
150 и выше |
10 |
130-140 |
6 |
|
|
140-150 |
4 |
|
|
150-160 |
2 |
|
|
Итого |
100 |
|
100 |
Произвести вторичную группировку рабочих предприятия №1, приняв за основу группировку рабочих предприятия №2.
Решение
Приведенные данные не дают возможности сравнивать распределение рабочих двух предприятий по степени выполнения норм выработки, так как данные сгруппированы по-разному. Поэтому необходимо эти ряды распределения привести к сопоставимому виду. За основу сравнения лучше взять распределение рабочих по предприятию №2 и перегруппировать рабочих предприятия №1, образовав такое же количество групп и с такими же интервалами, как и на предприятии №2.
Существует 2 способа образования новых групп:
1) Объединение (укрупнение) первоначальных интервалов. Применяется, когда границы старых и новых интервалов совпадают.
2) Способ долевой перегруппировки. Применяется, когда в ходе перегруппировки необходимо определить какая доля единиц совокупности перейдет из старых групп в новые.
В нашем примере в первую группу (до 100%) войдут две группы рабочих предприятия №1, сумма частот которых равна 8% (3 + 5).
Численность второй группы совпадает с третьей группой предприятия №1, поэтому в нее войдут 45%.
Численность
третьей группы составляет 110-125%, в нее
войдет полностью частота, равная 25%,
четвертой группы (110-120%) предприятия №1
и половина пятой группы
,
которая равна
.
Таким образом, частота третьей группы
(110-125%) составит 25 + 5 = 30%.
В четвертую группу (125-150%) войдут оставшиеся 5 + 6 + 4 = 15, в пятую группу (150 и выше) – 2%.
В результате проведенной группировки получены следующие сопоставимые данные (таблица 2.2).
Таблица 2.2 – Вторичная группировка рабочих по проценту выполнения норм выработки
Группа рабочих по проценту выполнения норм выработки, % |
Количество рабочих, % к итогу |
|
предприятий №1 |
предприятия №2 |
|
До 100 |
8 (3 + 5) |
5 |
100-110 |
45 |
25 |
110-125 |
30
(25 +
|
40 |
125-150 |
15 ( + 6 + 4) |
20 |
150 и выше |
2 |
10 |
Итого |
100 |
100 |
)
Полученная группировка показала, что на предприятии №2 значительно выше процент выполнения норм выработки рабочими.
Пример 3
Имеются следующие данные о тарифных разрядах 50 рабочих одного из цехов завода (таблица 3.1).
Таблица 3.1 – Данные о тарифных разрядах рабочих
3 |
5 |
6 |
3 |
2 |
4 |
3 |
5 |
5 |
6 |
4 |
3 |
2 |
3 |
4 |
5 |
4 |
2 |
4 |
6 |
5 |
3 |
4 |
5 |
4 |
3 |
3 |
6 |
2 |
3 |
4 |
6 |
3 |
4 |
4 |
5 |
4 |
5 |
3 |
4 |
2 |
6 |
3 |
4 |
5 |
3 |
4 |
4 |
5 |
4 |
Построить дискретный вариационный ряд по тарифному разряду и изобразить его графически.
Решение
1 Чтобы показать распределение рабочих по тарифному разряду, построим вариационный ряд, для чего выпишем все значения признака (тарифного разряда) в порядке возрастания по одному разу и подсчитаем число рабочих в каждой группе (таблица 3.2).
Таблица 3.2 – Группировка рабочих по тарифному разряду
Тарифный разряд (варианта
|
Численность рабочих (частота
|
2 |
5 |
3 |
13 |
4 |
16 |
5 |
10 |
6 |
6 |
Всего |
50 |
)
)
Это дискретный вариационный ряд, у которого вариантами являются значения тарифного разряда, а частотами – число рабочих.
2 Чтобы изобразить дискретный вариационный ряд графически, построим полигон частот (рисунок 3.1). Для этого используем прямоугольную систему координат, по оси абсцисс которой отложим значения тарифного разряда, а по оси ординат – число рабочих.
Рисунок 3.1 – Полигон распределения 50 рабочих
по тарифному разряду
Пример 4
Имеются данные о стоимости основных фондов у 50 предприятий (таблица 4.1).
Таблица 4.1 – Стоимость основных фондов 50 предприятий
(млн руб.)
9,4 |
8,0 |
6,3 |
10,0 |
15,0 |
8,2 |
7,3 |
9,2 |
5,8 |
8,7 |
5,2 |
13,2 |
8,1 |
7,5 |
11,8 |
14,6 |
8,5 |
7,8 |
10,5 |
6,0 |
5,1 |
6,8 |
8,3 |
7,7 |
7,9 |
9,0 |
10,1 |
8,0 |
12,0 |
14,0 |
8,2 |
9,8 |
13,5 |
12,4 |
5,5 |
7,9 |
9,2 |
10,8 |
12,1 |
12,4 |
12,9 |
12,6 |
6,7 |
9,7 |
8,3 |
10,8 |
15,0 |
7,0 |
13,0 |
9,5 |
Построить интервальный вариационный ряд по стоимости основных фондов, образовав 5 групп с равными интервалами по принципу «включительно», и изобразить его графически.
Решение
1 Чтобы показать распределение предприятий по стоимости основных фондов, сначала решим вопрос о величине интервала в группе, определив ее по формуле
млн
руб.,
где , – максимальное и минимальное значение признака;
– число образуемых групп.
Выделим теперь группы с интервалом 2 млн руб. и подсчитаем число предприятий в каждой группе (таблица 4.2).
Таблица 4.2 – Группировка предприятий по стоимости основных фондов
Стоимость основных фондов, млн руб. |
Число предприятий (частота) |
Накопленная (кумулятивная) частота F |
5-7 |
9 |
9 |
7-9 |
16 |
25 |
9-11 |
11 |
36 |
11-13 |
8 |
44 |
13-15 |
6 |
50 |
Всего |
50 |
- |
Это интервальный вариационный ряд с равными интервалами. При такой записи непрерывного признака, когда одна и та же величина встречается дважды (как верхняя граница одного интервала и как нижняя граница другого интервала), единица, обладающая этим значением, относится либо к той группе, где эта величина выступает в роли верхней границы (принцип «включительно»), либо – нижней границы (принцип «исключительно»). Так, в нашем примере предприятие со стоимостью основных фондов 9 млн руб. по принципу «включительно» отнесено ко второй группе, а не к третьей.
П
р и м е ч а н и е. Если вопрос о количестве
выделяемых групп, а следовательно, и о
величине интервала вызывает сомнение,
то рекомендуется использовать формулу
Стерджесса, предусматривающую выделение
оптимального числа групп (
)
при заданной численности совокупности
(
).
В
рассматриваемом примере это составило
бы
,
т.е. можно было выделить семь групп
предприятий (6,644 = 7) с равными интервалами
1,5 млн руб.
2 Чтобы изобразить данный ряд графически, построим гистограмму частот (рисунок 4.1). Для этого на оси абсцисс отложим величины интервалов, а по оси ординат – число предприятий (так как интервалы равны).
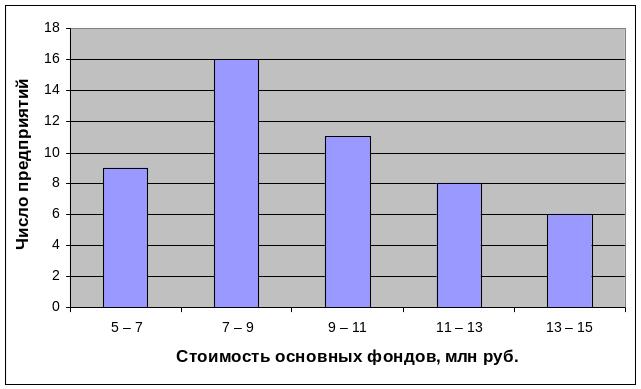
Рисунок 4.1 – Гистограмма распределения 50 предприятий
по стоимости основных фондов
Пример 5
Имеются следующие данные об успеваемости 20 студентов группы по статистике (таблица 5.1).
Таблица 5.1 – Данные об успеваемости студентов
5 |
4 |
4 |
4 |
3 |
2 |
5 |
3 |
4 |
4 |
4 |
3 |
2 |
5 |
2 |
3 |
3 |
2 |
3 |
3 |
Построить ряд распределения студентов по уровню успеваемости, выделив две группы студентов: неуспевающие (2 балла) и успевающие (3 балла и выше).
Решение
В основу группировки положен качественный признак, следовательно, количество групп определено числом разновидностей этого признака, а именно, таких групп будет две. Выпишем эти группы и подсчитаем число студентов в каждой группе (таблица 5.2).
Таблица 5.2 – Группировка студентов группы по уровню успеваемости
Группы студентов по уровню успеваемости |
Число студентов |
Неуспевающие |
4 |
Успевающие |
16 |
Итого |
20 |
Полученный ряд распределения является атрибутивным, так как построен по качественному признаку.