2.2. Канонические уравнения и схема автомата
Данные представления автоматов, в отличие от рассмотренных выше, дают представление о физической структуре автоматов.
1. Канонические уравнения.
Определение. В том случае, если функции выходов F
305
и переходов G автомата Мили задают в аналитической форме, то полная система уравнений называется канони-ческими уравнениями автомата. Для инициального автомата Мили они имеют вид:
z
m
(t
i
)
= F(x
n
(t
i
),
q k
(t
i-1
));
q k (t i ) = G(x n (t i ), q k (t i-1 ));
q k (t0 ) =q k0 .
П ример 1. Зададим при помощи канонических урав-нений инициальный автомат Мили, имеющий один дво-ичный вход x, один двоичный выход z и одно возможное двоичное состояние q:
z = x q(t i-1 );
q(ti ) = x & q(t i-1 );
q(t0 ) = 0.
Пример 2. Найти таблицу состояний для инициально-го автомата Мили, заданного в Примере 1 каноническими уравнениями.
Решение. Входными переменными таблицы принимаем ве-личины x(ti-1) и q(ti-1 ), выходными – z(ti) и q (ti). Для упро-щения вида таблицы обозначаем: x(ti-1) = х и z(t i ) = z.
В двух крайних левых столбцах, соответствующих x и q(ti-1), перечисляем в лексикографическом порядке все воз-можные их значения истинности. В крайних правых столб-цах, соответствующих z и q (t i-1 ) – значения функций и & (по каноническим уравнениям).
В итоге после добавления начального состояния полу-чаем следующую таблицу состояний:
-
x
q(ti-1)
z
q(t i )
0
0
0
0
0
1
1
0
1
0
1
0
1
1
1
1
q(t0 ) = 0.
306
Граф переходов автомата с цифровыми обозначения-ми множеств Q, Х, Z наиболее просто строить по двоичной таблице состояний.
Пример 3. Построить граф переходов инициального автомата Мили, заданного таблицей состояний в Примере 2.
Решение. Поскольку внутренних состояний два: q=0 и q=1, то отмечаем две вершины. Дуги, выходящие из вершины q=
0 со значениями x=0 и x=1 возвращаются в неё же со зна-чениями z=0 и z=1. Дуги, выходящие из вершины q=1 со значениями x=0 и x=1 возвращаются в вершины q=0 и q=1 со значениями z=1 (Рис.5.13).
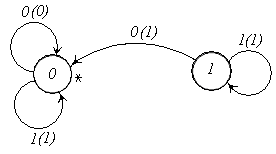
Рис.5.13
2.Схема автомата.
Определение. Схемой автомата Мили называется изо-бражение его физической структуры, осуществляющей пре-образование логической информации в соответствии с кано-
ническими уравнениями. Для запоминания внутренних со-стояний используется элемент “задержка”, имеющий один вход и один выход. Его назначение заключается не в изменении информации, подаваемой на вход, а во времен-ном сдвиге её на один такт назад: при подаче на вход в мо-
менты времени t0 , t1 ,…, tn значений q(t0 ) ,q (t1 ),…, q( tn ) он в последующие моменты времени t1 , t2 ,…, tn+1 будет выдавать эти же значения:
З( ti) = q( ti-1 ) .
307
Построение схемы производят по каноническим урав-нениям, поскольку она указывает их физическую реали-зацию.
Пример 4. Построить схему инициального автомата Мили, заданного в Примере 1 каноническими уравнениями.
Решение. Схема имеет вид, аналогичный обычной функ-циональной схеме с той разницей, что выход q(ti ) соединен со входом q(ti-1) элементом “задержка” (Рис.5.14).
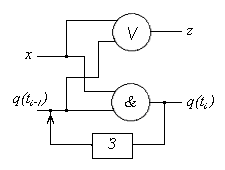
Рис.5.14
Канонические уравнения и схема автомата указывают структуру автомата, выполняющего требуемые преобразо-вания. Поскольку канонические уравнения и структура автомата по заданной таблице состояний может быть задана неоднозначно, то для определенности решения задачи необ-ходимо накладывать на искомую структуру дополнитель-ные требования.
Задачи.
1-6. Закодировать множества Q, Х, Z в двоичной системе и построить двоичные таблицы состояний для автоматов из Задач 1-6 п.1.1.
7-10. Закодировать множества Q, Х, Z в двоичной системе и построить двоичные таблицы состояний для автоматов из Задач I.1-4 п.1.4.
308
11. Построить канонические уравнения и схему автомата с одним двоичным входом, одним двоичным внутренним со-стоянием и двумя двоичными выходами, описывающими сумму входа с внутренним состоянием. Состояние инвер-тируется при входе, равном 0, и сохраняется при входе 1.