1.3. Реакция, эквивалентность и сокращение автоматов

Наряду с непосредственным заданием автоматов при помощи графа переходов и таблицы состояний их можно уподобить “черному ящику”, который перерабатывает вход-ную информацию в выходную. Рассмотрим более подробно два эти вида информации и особенности её автоматной об-работки.

Пусть задан некоторый автомат Мили А, у которого известны: множество возможных входов Х = (Х₁,Х₂,…,Х_N) и множество возможных выходов Z = (Z₁,Z₂,…,Z_M).

Определение. Входным словомХ длины k автомата Мили назовём упорядоченную последовательность элемен-тов из множества возможных входов Х, поступающих на вход автомата в моменты времени t₁ , t₂, …, t_k. Множество всех таких слов обозначим через Х^k. Множество всех вход-ных слов конечной длины обозначим через . По аналогии множество всех возможных выходных слов конечной длины обозначим через .

Многие свойства автоматов наиболее просто иллюст-рируются на автономных автоматах, у которых множество

286

входов Х состоит из одного элемента а (Х = 1) и, соот-ветственно, все множества Х^k имеют один элемент - а^k. На Рис.5.3 дан граф переходов автономного автомата с входом Х = (а), с P внутренними состояниями Q = (Q₁, Q₂, …, Q_P) и множеством возможных выходов Z = (y,z).

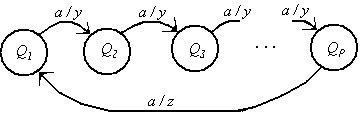
Рис.5.3

Очевидно, конечный результат работы автомата А за-висит не только от того, какое словоХ подано на его вход, но и от начального состояния автомата Q(t₀).

Определение. Выходным словомZ(Х,Q(t₀)), соответ-ствующим входному словуХ длины k и начальному состоя-нию автомата Q(t₀), называется последовательность эле-ментов из множества возможных выходов Z, поступившая

на выход автомата в моменты времени t₁ , t₂, …, t_k.

Зависимость Z(Х,Q(t₀)) задает автоматное отображе-ние из множества возможных входов в множество всех возможных выходных слов . Его основные свойства сле-дующие.

1. Свойство сохранения длины. ВходноеХ и выходное сло-ваZ =Z(Х,Q(t₀)) имеют одинаковую длину по количеству элементов множеств Х и Z. При этом один элемент в данных множествах может кодироваться несколькими символами, поэтому с точки зрения кодирующих символов входное и выходное слова могут иметь различную длину .

287

2. Отсутствие предвосхищения. Символы выходного слова Z, выдаваемые в моменты времени t₁, t₂, …, t_k, зависят только от начального состояния Q(t₀) и символов входного словаХ в моменты t₁, t₂, …, t_k. Зависимость от символовХ входного слова, вводимых в последующие моменты t_k+1, t_k+2, …, отсутствует.

Пример 1. Построить выходное словоZ =Z(Х, Q(t₀)), соответствующее входному словуХ = (Х(t₁), Х(t₂), Х(t₃), Х(t₄))= abab и начальному состоянию Q₂, для ав-томата, граф переходов которого дан на Рис. 5.4.

Рис.5.4

Решение. Поочередно рассматривая моменты времени, по-лучим:

1. t₁ : Q(t₁)= Q₁, Z(t₁)= x,

2. t₂ : Q(t₂)= Q₁, Z(t₂)= z,

3. t₃ : Q(t₃)= Q₂, Z(t₃)= z,

4. t₄ : Q(t₄)= Q₃, Z(t₄)= y.

Записывая подряд значения Z(t₁) - Z(t₄), получаем ответ:

Z(abab, Q₂)=xzzy.

288

Определение. Автоматное отображение из множест-ва возможных входов в множество всех возможных вы-ходных слов , получаемое при использовании автомата А с начальным состоянием Q_i = Q(t₀)  Q, называется реакци-

ей состояния Q_i и обозначается А(Q_i, ). Объединение ре-акций всех состояний Q_i  Q автомата называется реакцией автомата и обозначается А( ). Если в качестве множества входных слов взять все слова Х^k длины k, то получаемые множества всех выходных слов назовем, соответственно, для фиксированного состояния и всего автомата реакциями глубины k и будем обозначать через А(Q_i, Х^k) и А (Х^k) .

На практике реакции глубины k состояний Q_i автомата А можно представить в виде таблицы, у которой слева перечислены все входные слова из множества слова Х^k, а справа в соответствующих колонках – искомые реакции А(Q_i, Х^k) глубины k для всех внутренних состояний автомата Q_i. Для краткости данную таблицу будем называть таблицей реакций состояний автомата глубины k .

Пример 2. Построить для автомата, заданного графом переходов (Рис.5.4), таблицу реакций состояний глубины 2.

Решение. В левом столбце перечислим все возможные вход-ные слова длины 2, справа приведем реакции глубины 2 состояний автомата Q₁, Q₂, Q₃. В итоге получим следующую таблицу:

X2={Х(t1) Х(t2)}	Z 2 = {Z(t1) Z(t2)}
	Q1	Q2	Q3
Aa	zx	xz	xz
Ba	zz	yz	yz
Ab	zy	xz	xz
Bb	zz	yy	yy

289

Рассмотрим, каким образом информация о реакциях состояний автомата может быть использована для оптими-зации его структуры.

Определение. Допустим, автоматы А и А имеют оди-наковые множества возможных входов Х и Х и множества возможных выходов Z и Z. Внутренние состояния Q_i и Q_j автоматов А и А называют эквивалентными, если их реак-ции А(Q_i, ) и А(Q_j, ) совпадают. Автоматы А и А назы-вают эквивалентными, если их реакции А( ) и А( ) сов-падают. По аналогии с реакциями состояния и автоматы, у которых совпадают реакции глубины k, будем называть k- эквивалентными.

Замечание 1 . Введенные определения эквивалентных состояний верны и в том случае, когда А = А, т.е. рассмат-риваются различные состояния одного автомата.

Замечание 2 . Введенные определения эквивалентных и k- эквивалентных состояний и автоматов можно рассмат-ривать как бинарные отношения на соответствующих мно-жествах внутренних состояний и множествах автоматов. Несложно проверить, что они удовлетворяют всем аксио-мам отношения эквивалентности: рефлексивности, симмет-ричности и транзитивности. Отношения эквивалентности и k- эквивалентности разбивают множество всех внутренних состояний Q любых автоматов с одинаковыми множествами Х и Z на непересекающиеся классы эквивалентности.

Обозначим разбиение множества всех внутренних со-стояний Q автомата А на классы k - эквивалентности через {Q}^k =Q^k,1,…, Q^k,s . По определению эквивалентности

1)Q^k,1 … Q^k,s = {Q}^k,

2)Q^k,i {Q}^k,Q^k,j {Q}^k, ij  Q^k,i Q^k,j = .

Очевидно, если множество классов эквивалентности Q¹ , …, Q^s содержит некоторый класс Q^р (1рs) , в котором более одного состояния - Q^р =( Q_р1, Q_р2 ,… ), то все состоя-

290

ния в Q^р могут быть заменены одним, имеющим одина-ковую реакцию с ними. Новый полученный автомат будет эквивалентен прежнему, но его структура упростится за счет уменьшения числа внутренних состояний.

Определение. Автомат А называют сокращенным, ес-ли все пары его внутренних состояний не являются экви-валентными.

У сокращенного автомата полностью проведена опи-санная выше процедура замены классов эквивалентных со-стояний одним представителем.