40. Подпространства в векторных пространствах. Простейшие свойства и примеры.

П одпространством линейного пространства V над полем F=(R) называют такое подмножество , которое обладает свойствами:

Другими словами, векторным подпространством пространства V над полем F=(R) называют подмножество U из V , замкнутое относительно действий «сложения» и «умножения» на скаляр, определённых в V.

41. Система образующих или порождающее семейство векторов. Простейшие свойства. Примеры.

42. Линейная комбинация векторов, Линейная зависимость и линейная независимость векторов. Определения и простейшие свойства. Примеры.

Линейной комбинацией векторов называют вектор

при некоторых коэффициентах

С овокупность векторов называется линейно зависимой (ЛЗС), если найдутся числа , не равные нулю одновременно, такие, что выполняется равенство:

В противном случае совокупность называется линейно независимой (ЛНС).

Пример:

Покажем, что система многочленов

линейно независима.

Действительно,

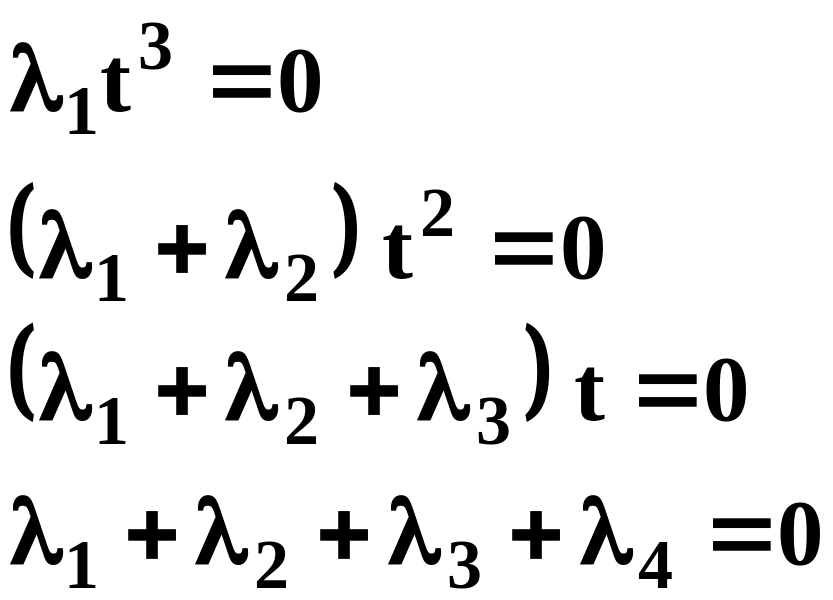
П окажем, что система столбцов

линейно зависима.

Д ействительно,

Очевидно, что полученная СЛУ имеет нетривиальные решения

Н апример,

43. Базис и размерность векторного пространства. Три эквивалентных определения базиса. Свойства и примеры.

П усть - произвольное множество векторов линейного пространства V над полем F=(R). Упорядоченная система векторов

называется базисом в Q, если:

а )

б ) система линейно независима;

в ) для любого найдутся такие числа , что

В этом случае числа называются координатами вектора x в базисе

Все базисы пространства V над полем R имеют одинаковое число векторов, которое называется размерностью векторного пространства V и обозначается

Примеры базисов пространства:

1 .

2.

44. Координаты вектора в фиксированном базисе. Изменение координат вектора при замене базиса. Примеры.

45. n – мерное пространство . Простейшие свойства и примеры подпространств в

46. Векторное пространство матриц фиксированного размера с вещественными коэффициентами . Базис и размерность данного пространства. Примеры подпространств.

47. Сумма и пересечение подпространств. Формула для размерности подпространств, их суммы и пересечения. Примеры.

48. Прямая сумма подпространств. Примеры.

49. Геометрия в n – мерном пространстве Длина вектора, угол между векторами, ортогональность векторов. Ортонормированный базис.

Длина вектора, угол между векторами:

Ортонормированным базисом называется базис, состоящий из попарно ортогональных векторов, каждый из которых имеет длину, равную единице.

50. Ортогональные матрицы и их простейшие свойства. Примеры.

51. Ортогональное дополнение к подпространству в . Свойства и примеры.

Ортогональным дополнением подпространства U из Rⁿ называется подпространство, состоящее из векторов, ортогональных любому вектору из U.

Свойства ортогонального дополнения:

52. Разложение пространства в прямую сумму подпространства и его ортогонального дополнения. Расстояние от вектора до подпространства. Угол между вектором и подпространством. Примеры.

53. Алгоритм нахождения базиса в подпространстве, порождённом конечной системой векторов в n – мерном пространстве

1. Столбцы, порождающие подпространство, записать в матрицу.

2. Элементарными преобразованиями над столбцами привести эту матрицу к «ступенчатому» виду.

3. Ненулевые столбцы данной «ступенчатой» матрицы и будут составлять базис исходного подпространства, а ранг матрицы будет равен размерности этого подпространства.

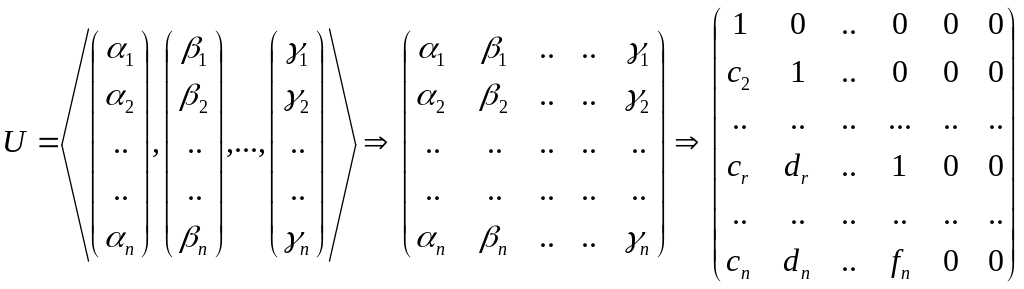
54. Ранг матрицы, как размерность линейной оболочки столбцов. Свойства, примеры.

55. Определение и простейшие свойства вещественных квадратичных форм. Примеры.

56. Матричная запись квадратичной формы. Преобразование матрицы квадратичной формы при линейной замене переменных. Примеры.

М атричной записью квадратичной формы называется следующее выражение:

57. Теорема Лагранжа о приведении квадратичной формы к диагональному виду. Примеры.

Любую вещественную квадратичную форму невырожденным линейным преобразованием переменных можно привести к диагональному виду, т.е. когда преобразованная квадратичная форма будет состоять только из квадратов новых переменных с некоторыми коэффициентами.

Примеры:

58. Теорема об ортогональном приведении квадратичной формы к диагональному виду. Примеры.

Любую вещественную квадратичную форму можно привести к диагональному виду при помощи линейного преобразования переменных с ортогональной матрицей.

Пример:

59. Определение и простейшие свойства положительно определённых квадратичных форм. Примеры.

Квадратичная форма называется положительно определенной, если все ее значения при вещественных значениях переменных, не равных одновременно нулю, положительны.

Т еорема. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы после приведения ее к диагональному виду все коэффициенты при квадратах новых переменных были положительны.

60. К ритерий Сильвестра для положительно определенных квадратичных форм. Примеры.

Закон инерции вещественных квадратичных форм. Примеры¹.

61. Задача о паре форм. Примеры.

62. Примеры использования пакета «Математика-5.*» при решении задач линейной алгебры.

1 Факультатив.