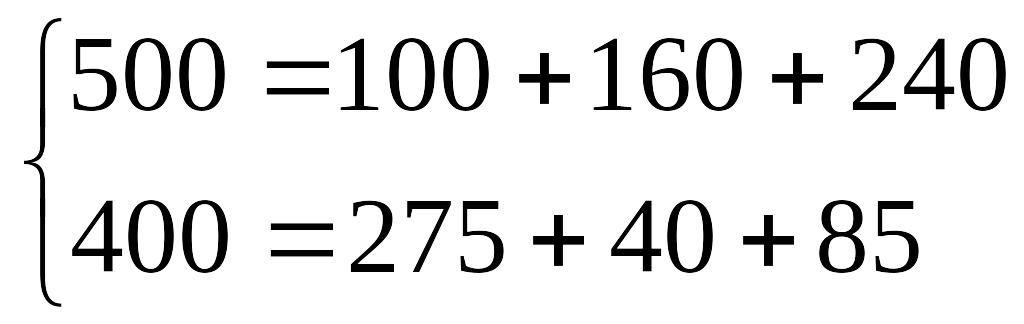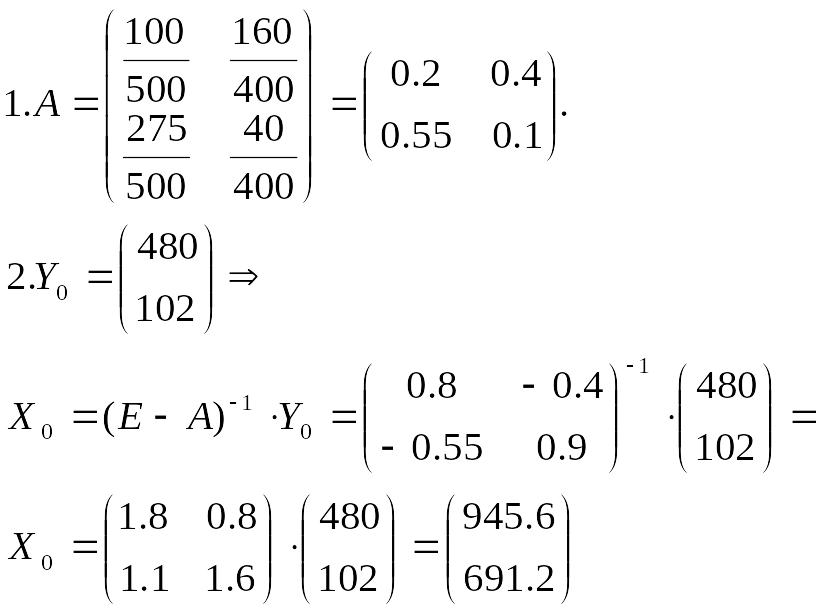24. Обратная матрица. Теорема о существовании и единственности обратной матрицы. Свойства обратной матрицы. Примеры.

Квадратная матрица А называется обратимой – если найдётся квадратная матрица В, что выполняются равенства:

А* В = В * А = Е

В этом случае матрица В называется обратной к матрице А и обозначается

В = А^-1

Теорема

Для того чтобы для матрицы А существовала обратная, необходимо и достаточно, чтобы определитель матрицы был отличен от нуля, т.е. чтобы А была невырожденной. При этом

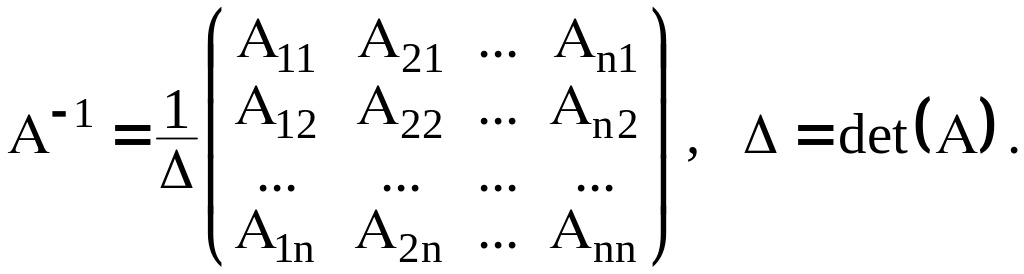
Свойства:

Е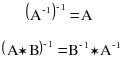 сли квадратные матрицы А и В обратимы, то справедливы следующие соотношения:

25. Определитель Вандермонда. Определение и простейшие свойства. Примеры.

Матричный вид данных равенств:

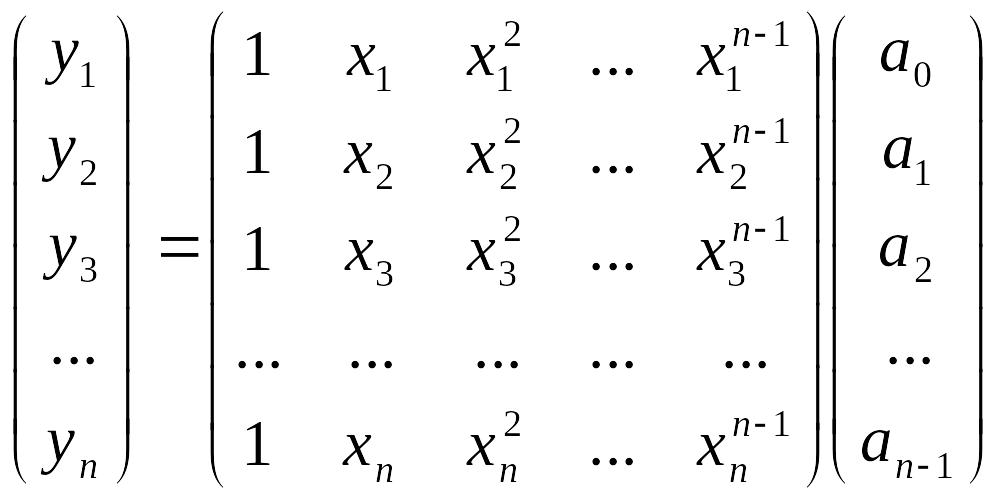
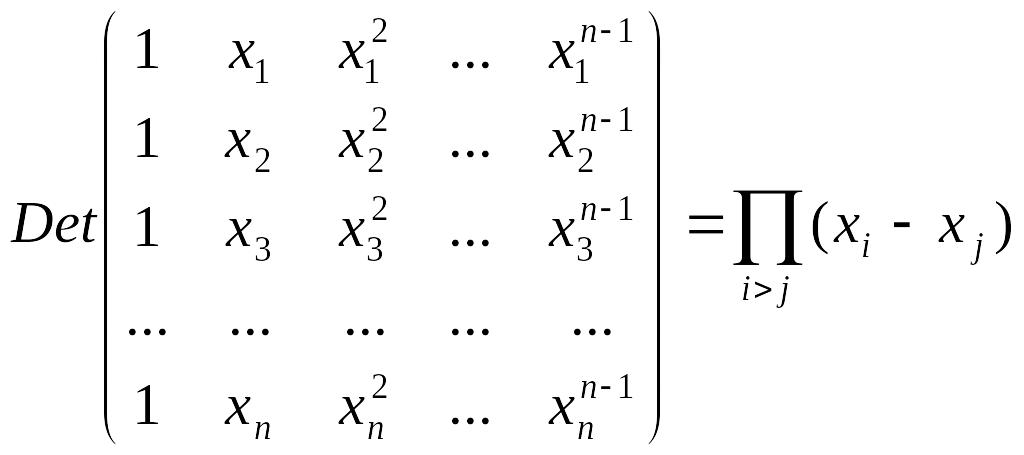
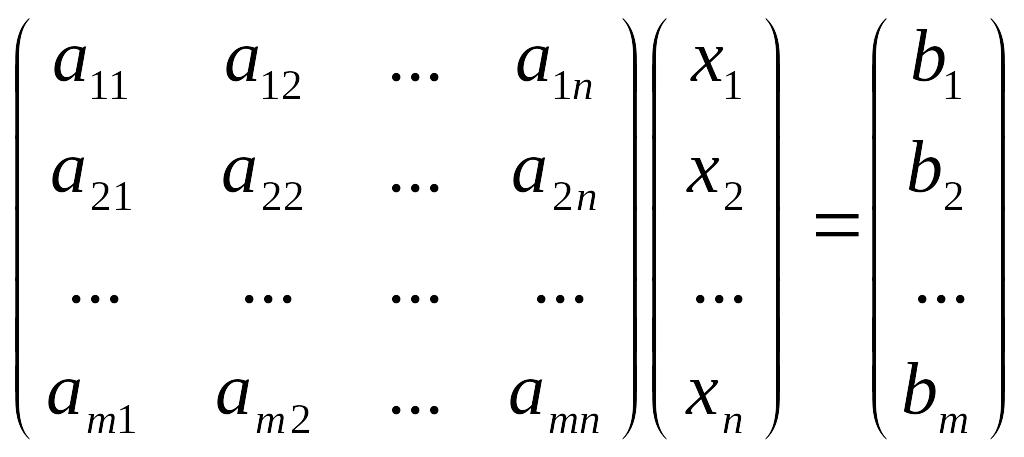
26. Определение системы линейных уравнений. Решение слу. Равносильность. Совместимость. Матричная запись слу. Простейшие свойства и примеры.

П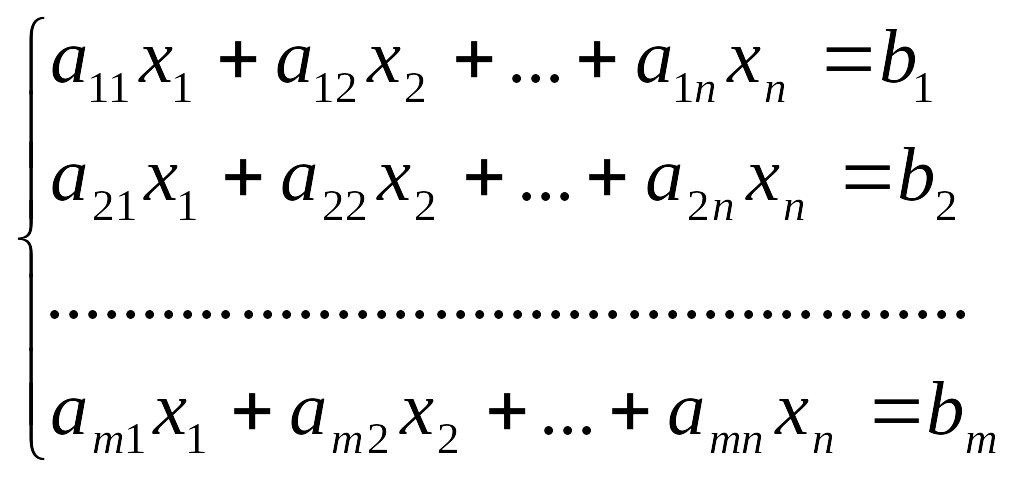 од системой линейных уравнений (СЛУ) мы будем понимать следующую запись:

г де - «неизвестные» системы,

- коэффициенты системы, m – число уравнений, n - число неизвестных

Р ешением (одним) СЛУ называется последовательность чисел

удовлетворяющая всем уравнениям системы, т.е. обращающая их в верные числовые равенства:

Возможно не надо, но всё же. Матрица коэффициентов системы, столбец свободных членов системы, столбец неизвестных (переменных) системы:

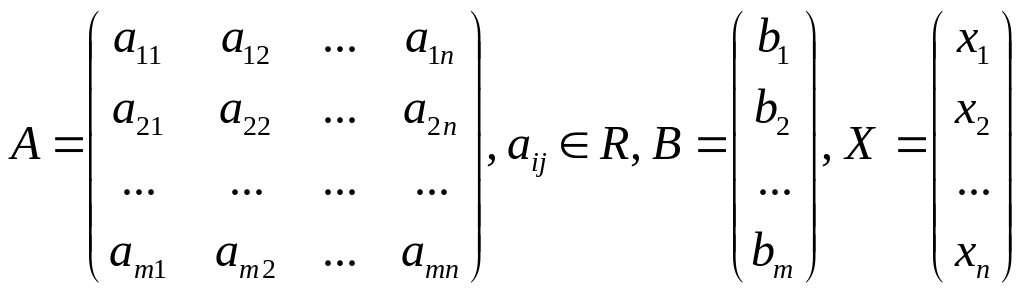
Матричная запись слу

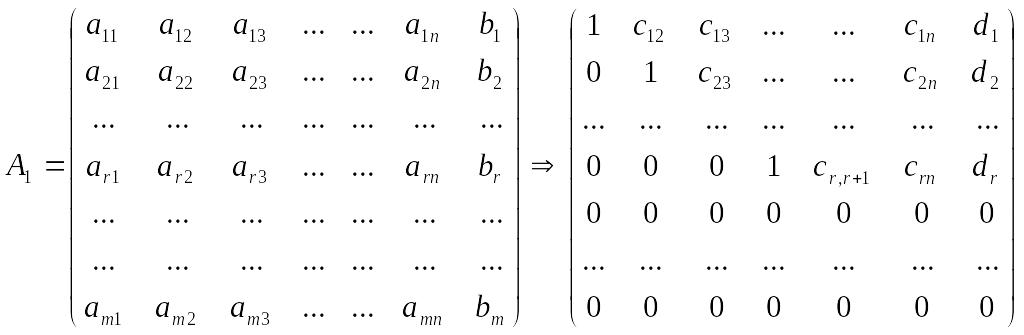
27. Метод Гаусса решения систем линейных уравнений. Примеры.

Метод Гаусса заключается в приведении расширенной матрицы данной СЛУ элементарными преобразованиями над строками, к некоторому специальному виду (почти трапециевидному) - прямой ход схемы Гаусса, и нахождению затем множества решения системы с полученной расширенной матрицей (эта система равносильна исходной) - обратный ход схемы Гаусса.

28. Теорема Кронекера-Капелли. Примеры.

Система линейных уравнений совместна (т.е. имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы коэффициентов равен рангу расширенной матрицы системы, т.е.

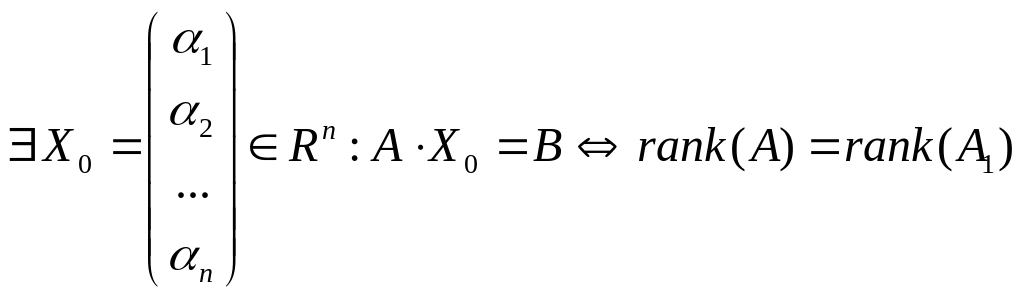
На «языке» векторных пространств:

СЛУ совместна тогда и только тогда, когда подпространство порождённое столбцами матрицы коэффициентов совпадает с подпространством, порождённым столбцами расширенной матрицы системы, т.е.

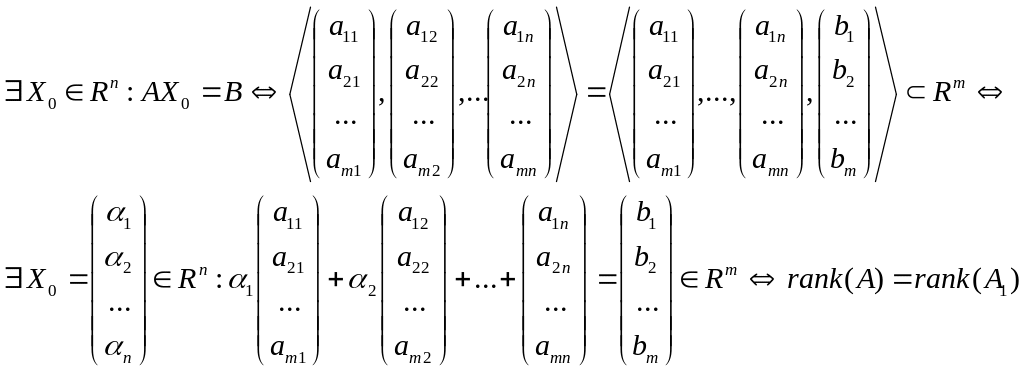
29. Теорема о числе решений системы линейных уравнений. Примеры.

Пусть дана совместная СЛУ от n неизвестных с матрицей коэффициентов ранга r . Тогда:

1. если r = n , то система имеет единственное решение;

2. если r < n , то система имеет бесконечно много решений, причем (n – r) неизвестным можно присвоить произвольные значения, а остальные r неизвестных выражаются через них единственным образом.

30. Однородные системы линейных уравнений. Примеры.

Пример:

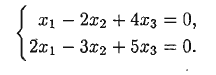
31. Структура множества решений СЛУ и соответствующей ОСЛУ с одинаковой матрицей коэффициентов. Примеры и геометрическая интерпретация.

32. Обратная матрица. Определение и простейшие свойства. Способ нахождения обратной матрицы как решение матричной задачи. Примеры.

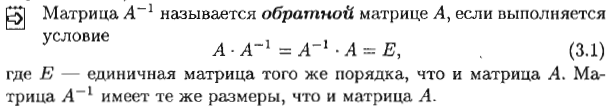
Свойства:

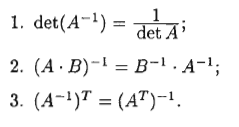
Способ нахождения обратной матрицы

33. Модель Леонтьева многоотраслевой экономики (модель межотраслевого баланса). Матрица прямых затрат. Матичная запись уравнения межотраслевого баланса. Примеры.

Р ассматривается n отраслей, каждая из которых производит свою продукцию.

Пусть - общий (валовый) объем продукции i-й о трасли;

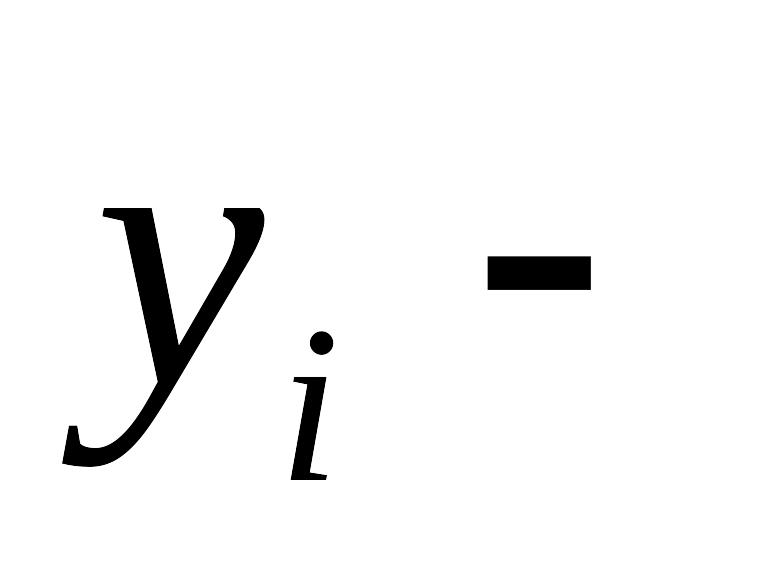объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства;

объем конечного продукта i-й отрасли для непроизводственного потребления.

Уравнение межотраслевого баланса:

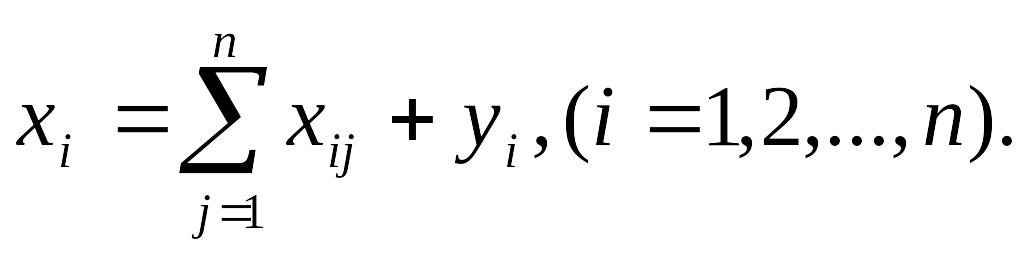
Рассматриваем стоимостной межотраслевой баланс. Определим матрицу коэффициентов прямых затрат:

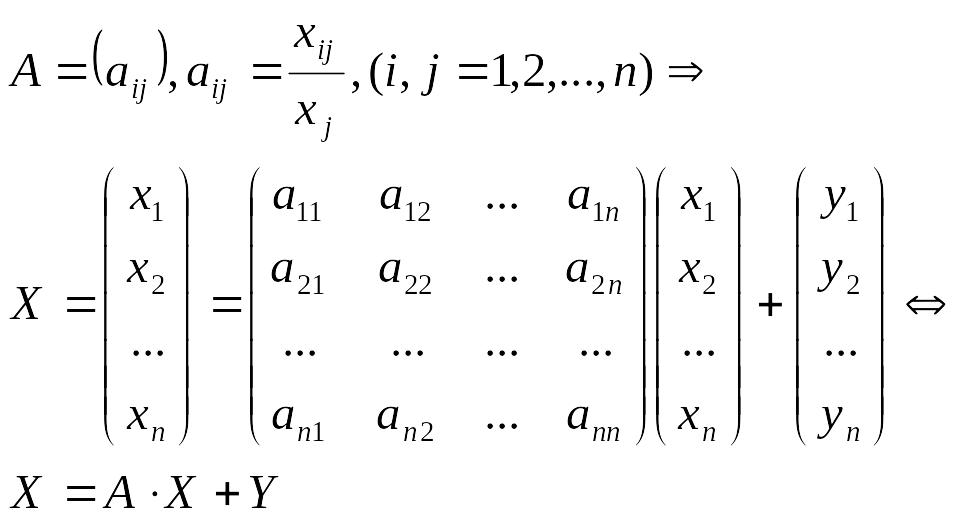
Пример

Дано уравнение межотраслевого баланса.

Найти:

1. Матрицу А - прямых затрат.

2. Вектор валового выпуска, если конечный продукт 1-й отрасли должен увеличиться вдвое, а 2-й – на 20%?

РЕШЕНИЕ: