13. Свойства определителя: Поведение определителя матрицы при элементарных преобразованиях строчек матрицы. Примеры.

Матрица определителя приводится элементарными преобразованиями над строками (или столбцами) к верхнетреугольному виду. Вычисляется определитель полученной матрицы с учетом сделанных преобразований.

Поведение определителя матрицы:

• При умножении строки на любое число отличное от 0, определитель умножается на это число.

• При прибавлении к одной строке другой умноженной на любое число определитель не изменяется.

• При перестановки строк местами определитель меняет знак на противоположный.

14. Определитель верхнетреугольной матрицы. Примеры.

Определитель верхнетреугольной матрицы равен произведению элементов главной диагонали.

П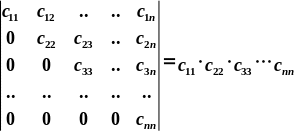 ример:

15. Алгебраические дополнения элемента матрицы. Разложение определителя по строке. Свойство ортогональности алгебраического дополнения. Примеры.

Алгебраическим дополнением элемента называется следующий определитель n-го порядка

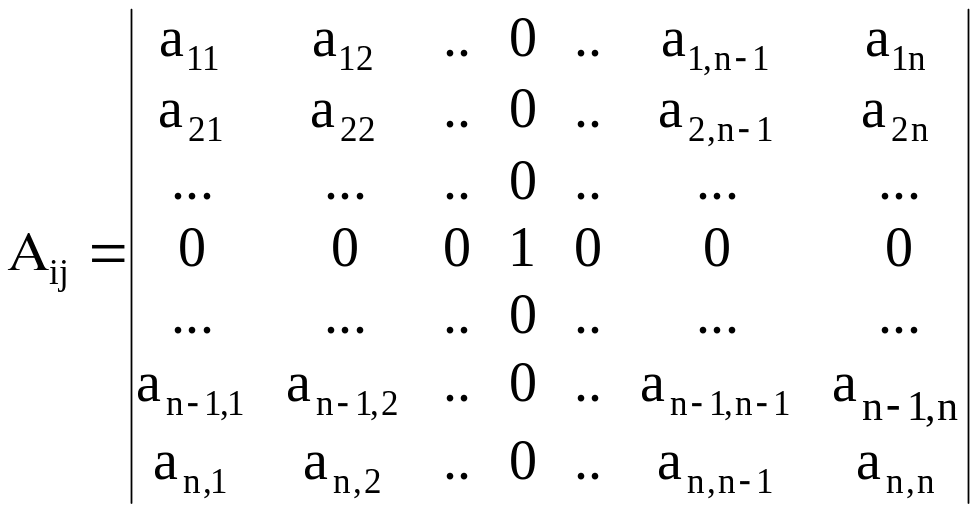
Сумма произведений элементов любой строки определителя на их алгебраические дополнения равна этому определителю, т.е.

16. Минор элемента квадратной матрицы и его связь с алгебраическим дополнением данного элемента матрицы. Примеры.

Минором элемента матрицы определителя n-го порядка, называется определитель (n-1)-го порядка, получающийся из исходного определителя вычеркиванием i-й строки и j-го столбца.

Справедливо следующее равенство

Т.е. минор отличается от алгебраического дополнения на (-1)^i+j

17. Понятие минора матрицы. Простейшие свойства и примеры.

Пусть произвольная матрица. В данной матрице выбираем произвольные r строк и r столбцов и строим из них квадратную матрицу размера r х r . Определитель такой матрицы и называется минором r–го порядка матрицы А.

18. Ранг матрицы. Определение и простейшие свойства. Примеры. Алгоритм вычисления ранга матрицы.

Простейшие свойства:

• если к матрице приписать строку или столбец из нулей, то ранг исходной матрицы не изменится.

• если в матрице все миноры k-го порядка равны нулю, то равны нулю и все миноры (k+1)-го порядка (если они существуют).

• при элементарных преобразованиях ранг матрицы не изменяется.

Алгоритм вычисления:

приведение матрицы к трапециевидному виду

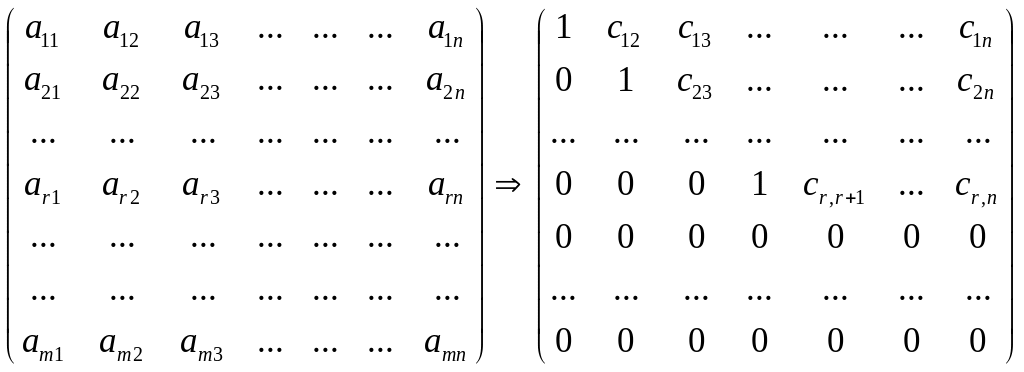
19. Характеристика ранга матрицы в терминах её миноров. Примеры.

20. Определитель ступенчатой матрицы. Простейшие свойства и примеры.

Определитель ступенчатой матрицы равен произведению определителей матриц, являющихся диагональными клетками исходной матрицы.

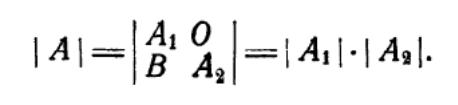
21. Мультипликативность умножения определителей. Примеры.

О пределитель произведения двух квадратных матриц равен произведению определителей этих матриц, т.е.

Пример:

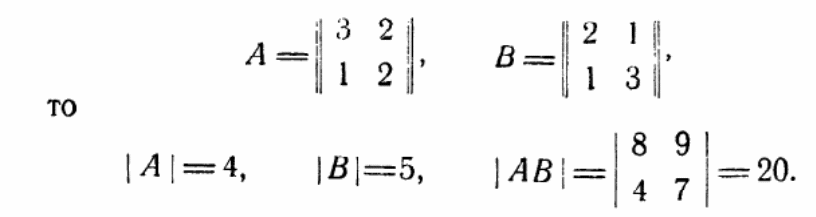
22. Связь между определителем и рангом матрицы. Примеры.

23. Взаимная матрица и её свойства. Примеры.

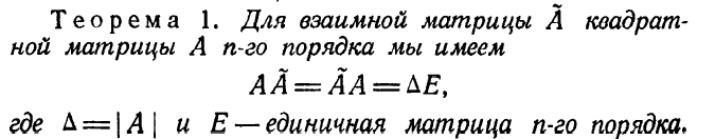
Взаимная матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц.

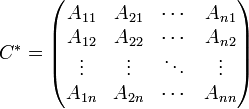
Исходная матрица:

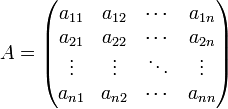
Где:

C * — взаимная матрица;

A_ij — алгебраические дополнения исходной матрицы;

a_ij — элементы исходной матрицы.