Элементарные сведения теории перестановок. Изменение четности перестановки при транспозиции. Примеры.
Перестановка называется чётной, если она содержит чётное число инверсий, и называется нечётной в противоположном случае.
Пример:
(2, 6, 1, 5, 3, 4) – так как инверсий – 7, то перестановка нечётная.
Определение и простейшие свойства определителя квадратной матрицы порядка n. Примеры вычисления определителей.
1.Умножение некоторой строки (столбца) матрицы определителя на некий коэффициент равносильно умножению самого определителя на этот коэффициент.
2.Если все элементы некоторой строки (столбца) матрицы равны нулю, то и определитель равен нулю.
3.Определитель не меняется при транспонировании (свойство равноправности строк и столбцов матрицы).
4.При перестановке двух строк (столбцов) местами определитель меняет знак на противоположный.
5.Определитель с двумя одинаковыми строками (столбцами) равен нулю.
6.Определитель с двумя пропорциональными строками (столбцами) равен нулю
7.Если в определителе некоторая строка есть сумма двух других строк, то определитель равен сумме двух определителей с этими строками, а все остальные строки этих определителей равны строкам исходного определителя.
П
ример:
8.Если к некоторой строке (столбцу) определителя прибавить другую строку (столбец), умноженную на произвольное число, то величина определителя не изменится.
9.Определитель верхнетреугольной матрицы равен произведению элементов главной диагонали.
П
ример:
10.Алгоритм вычисления определителя. Матрица определителя приводится элементарными преобразованиями над строками (или столбцами) к верхнетреугольному виду. Вычисляется определитель полученной матрицы с учетом сделанных преобразований.
11.Сумма произведений элементов любой строки (столбца) определителя на их алгебраические дополнения равна этому определителю
12.Сумма произведений элементов любой строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю
14.Определитель ступенчатой матрицы равен произведению определителей матриц, являющихся диагональными клетками исходной матрицы.
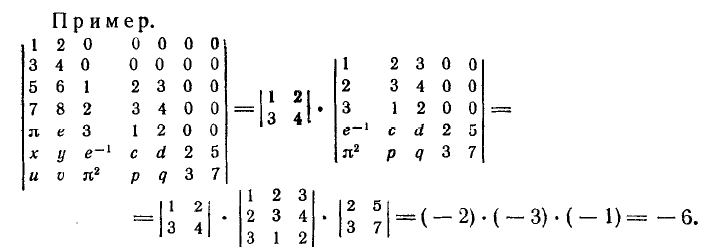
1
5.Определитель
произведения двух квадратных матриц
равен произведению определителей этих
матриц, т.е.
Пример:
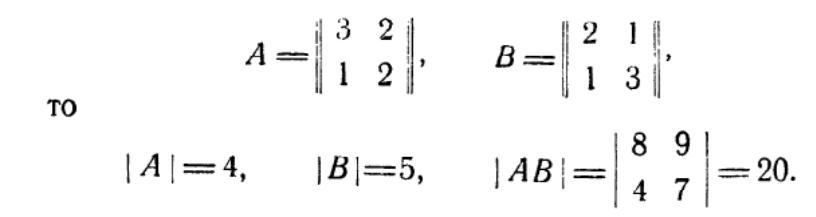
Свойства определителя: Общее правило знака. Определитель транспонированной матрицы.
Определитель не меняется при транспонировании (свойство равноправности строк и столбцов матрицы).
Свойства определителя: Определитель матрицы, строка которой есть сумма двух строк. Определитель матрицы, строка которой имеет общий множитель. Примеры.
Если в определителе некоторая строка есть сумма двух других строк, то определитель равен сумме двух определителей с этими строками, а все остальные строки этих определителей равны строкам исходного определителя.
П ример:
Если все элементы некоторой строки (столбца) содержат общий множитель, то его можно вынести за знак определителя.
П
ример:
Свойства определителя: Изменение определителя при перемене местами двух строк. Определитель матрицы с двумя одинаковыми строчками. Примеры.
При перестановке двух строк (столбцов) местами определитель меняет знак на противоположный.
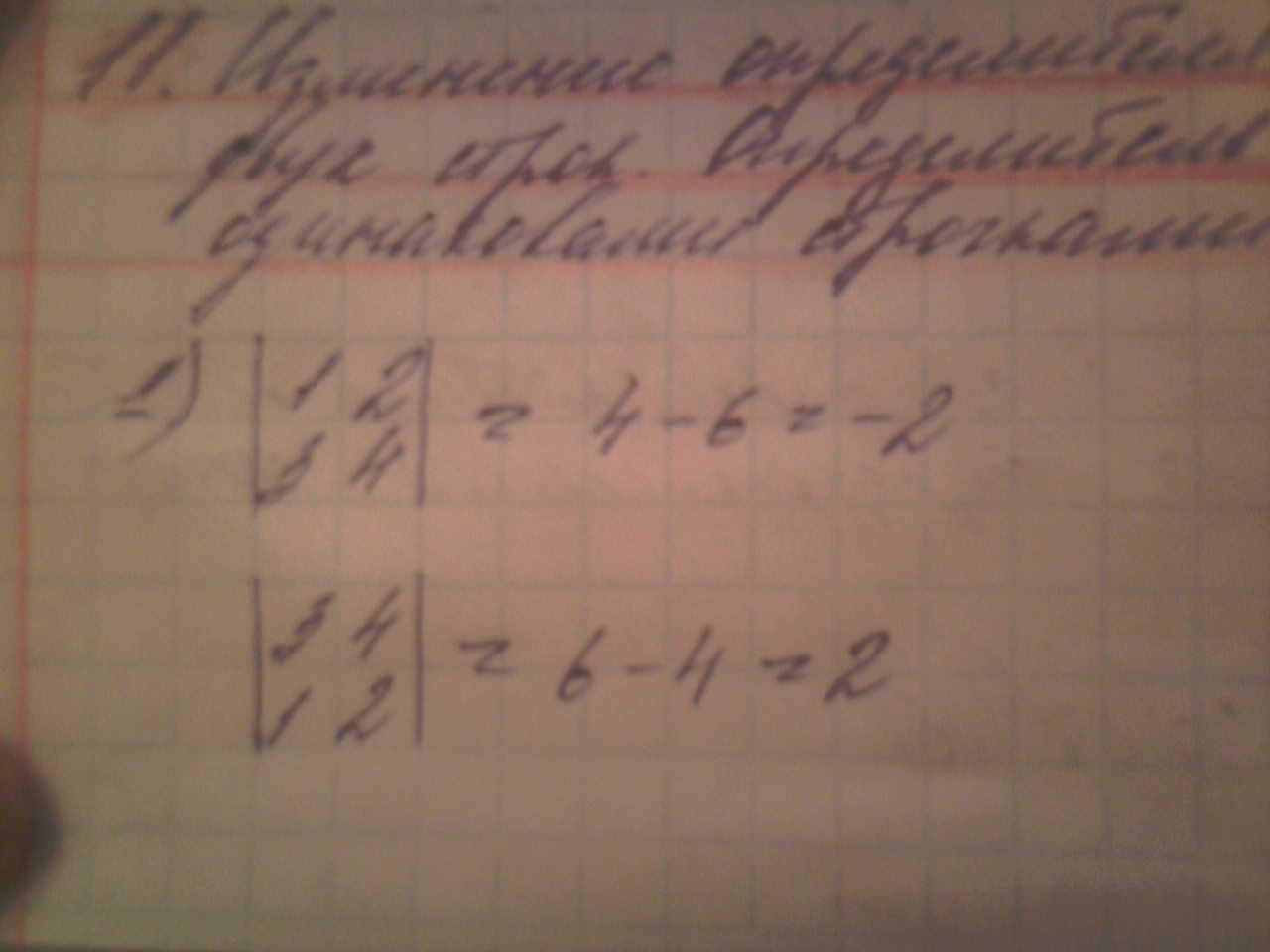
Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Элементарные преобразования матрицы. Их свойства. Трапециевидный вид матрицы. Примеры.
Преобразования:
умножение строки (столбца) на число, отличное от нуля;
прибавление к одной строке (столбцу) другой, умноженной на любое число;
перемена местами двух строк (столбцов).
Свойства:
