2.3. Существование равновесия в модели Неймана.

Невырожденное положение равновесия задаёт одновременно стационарные траектории и интенсивностей, и цен. Поэтому такая ситуация является самой простой для изучения.

Для всех 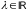рассмотрим задачу линейного программирования:

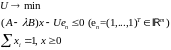14014\* MERGEFORMAT (.)

Обозначим через 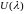решение задачи 014. Задача

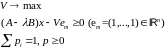15015\* MERGEFORMAT (.)

является двойственной для задачи 014, поэтому для ее решения справедливо равенство .

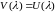Теорема 2.1. Тройка задает положение динамического равновесия (возможно – вырожденного) в модели Неймана тогда и только тогда, когда при 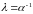выполняется условие 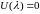и пары , 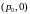являются решениями соответственно задач 014 и 015.

Доказательство. Пусть – положение равновесия в модели Неймана. Тогда неравенства 011 и 012 показывают, что пары , являются при допустимыми планами, соответственно, для задач 014 и 015. Поскольку значения целевых функций совпадают (и равны ), согласно теории двойственности эти пары являются решениями данных задач.

Доказательство второй части теоремы также не представляет труда.

Теорема 2.1 дает способ конструктивного отыскания положений динамического равновесия. Рассмотрим применение данного способа в одном из случаев. Справедлива следующая лемма.

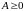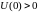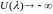Лемма 2.1. 1) Функция непрерывна на ; 2) Пусть , причем в матрице нет нулевых столбцов. Тогда ; 3) Пусть , причем в матрице нет нулевых строк. Тогда ; при ; 4) Пусть . Тогда – монотонная невозрастающая функция.

Доказательство. 1) Функция непрерывна по совокупности переменных. Множество 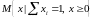замкнуто и ограничено. По условию задачи .

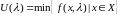2) При 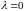основное ограничение задачи 014 имеет вид неравенства 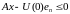, или для всех . Так как и 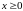, получаем 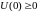. Для 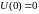необходимо существование , для которого 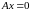. У вектора по условию есть хотя бы одна положительная координата 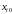. Если у матрицы столбец 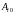не нулевой, условие не возможно.

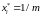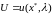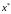3) Пусть для всех . Вычислим минимальное значение , при котором вектор будет допустимым (при этом, очевидно, ):

.

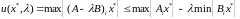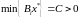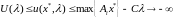Поскольку у матрицы нет нулевых строк и , то . Таким образом, при ;

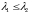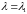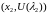4) Пусть , – решение задачи 014 при , – при 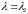. Тогда при

,

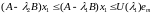т.е. пара является допустимой парой в задаче при . Следовательно, .

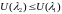Лемма доказана.

Теорема 2.2. Пусть , , в матрице нет ненулевых строк, в матрице нет ненулевых столбцов. Тогда в соответствующей модели Неймана существует положение равновесия.

Доказательство. Согласно доказанной лемме, в условиях теоремы функция , задающая оптимальное значение целевой функции в задаче 014, имеет точку , в которой . Согласно теореме 2.1 это означает существование положения равновесия , в котором 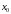и 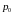– решения задач 014 и 015.

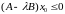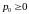Заметим, что , . Поскольку , , получим 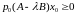, , 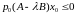откуда 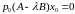, или .

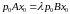2.4. Равновесие в модели динамического моб.

Рассмотренная в параграфе 2.1. модель динамического межотраслевого баланса была сведена к модели Неймана путём определения соответствующих матриц и (см. 07).

Однако в матрице есть отрицательные элементы, в матрице – нулевые столбцы и строки, поэтому к этой модели нельзя применять теорему 2.2 о существовании равновесия. Поэтому такую модель 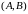называют не моделью Неймана, а моделью неймановского типа.

Будем считать, что темпу роста 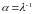соответствует луч Неймана 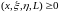, если 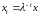, , 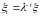, 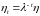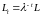– допустимый вектор в задаче МОБ.

Подставляя данный вектор в условия 01–05, получаем систему неравенств для нахождения луча Неймана:

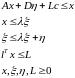. 16016\* MERGEFORMAT (.)

Найдём условия, при которых система условий 016 имеет нетривиальное решение.

Пусть 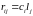, , 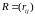, 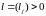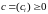. . 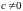Заметим, что в этом случае

.

Поэтому .

Попробуем найти решение, удовлетворяющее системе равенств

.

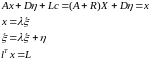Тогда , 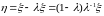. Первое равенство принимает вид:

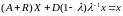, или 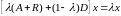. 17017\* MERGEFORMAT (.)

Предположим, что выполнены следующие условия:

1)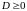 и (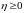 , 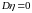) 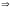( 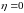) (всякое увеличение мощностей требует материальных затрат).

2) , число Фробениуса матрицы 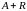меньше единицы (экономический смысл условия – технология, задаваемая матрицей , векторами и , позволяет каждому работающему «прокормить себя»).

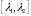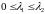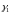Лемма 2.2. Пусть – квадратная неотрицательная матрица, непрерывно зависящая от на отрезке , . Пусть и 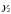– числа Фробениуса неотрицательной матрицы 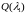и .

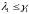Если и , то задача:

.

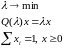имеем единственное решение , причём

1)  ;

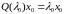2) 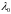 – число Фробениуса матрицы 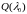, которому соответствует вектор ;

3)  и .

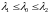Теорема 2.4. В модели 07 существуют положение равновесия с темпом роста , которому соответствует единственный луч Неймана 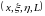, причём:

1)  – число Фробениуса матрицы .

2)  – правый вектор Фробениуса матрицы 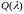, соответствующий ;

3)  , , .

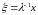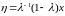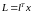Доказательство. Рассмотрим задачу:

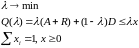. 18018\* MERGEFORMAT (.)

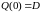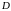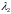; число Фробениуса матрицы больше нуля (по условию 1). ; число Фробениуса матрицы удовлетворяет условию .

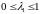Для доказательства теоремы воспользуемся доказанной леммой, согласно которой существует решение 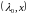уравнения 017, такое что 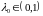. Выполнение условия 017 гарантирует выполнение условий 016 при , , . Теорема доказана.

Замечание 2.1. Рассмотрим набор двойственных переменных 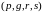для задачи 018. Тогда: 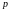– левый вектор Фробениуса для матрицы , ; ; .
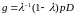
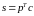