33. Локальный экстремум. Теорема Ферма

Пусть функция f задана на некотором множ-ве X  R и x0  X.

Определение.

Точка x0 называется точкой локального максимума (минимума) функции f, если сущ-ет такая окрестность U(x0) точки x0, что для всех x  X ∩ U(x0) выполняется неравенство f(x)>=f(x0) (cоответственно f(x)<=f(x0) )

Если для всех x  X ∩ U(x0) выполняется неравенство f(x)<f(x0) ( соотв. f(x)>f(x0) ), то точка x0 называется точкой локального максимума (минимума)

Точки максимума и минимума функции называют её точками экстремума

Необходимое условие экстремума

Если функция имеет в точке локального экстремума производную, то эта производная =0

Определение 2.

Если функция определена в некоторой окрестности точки x0 и в этой точке производная функции либо существует и равна нулю, либо не сущ-ет, то точка x0 называется критической точкой этой функции.

Определение3.

Точка x0 называется точкой возрастания (убывания) функции f, если у x0 существует такая окрестность U(x0), что при x  X ∩ U(x0), x<x0, выполняется неравенство f(x)<=f(x0) ( соотв. f(x)>=f(x0) ), а при x>x0 – неравенство f(x)>=f(x0) (соотв. f(x)<=f(x0) ).

Теорема ФЕРМА.

Пусть функция а задана на множ-ве X и x0  X.

Если функция определена в некоторой окрестности точки, принимает в этой точке наибольшее (наименьшее) значение и имеет конечную или определённого знака бесконечную производную, то эта производная =0

F(x)<=F(x0)

(f(x) – f(x0) / x – x0)>=0 если x<x0

(f(x) – f(x0) / x – x0)<=0 если x>x0

( lim (f(x) – f(x0) / x – x0) = f’(x0) )

x>>x0 ( f’(x0)>=0 или f’(x0)<=0 )

34 Теорема Ролля.

Теорема Ролля. Пусть функция y=f(x) непрерывна на [a, b] и дифференцируема на (a, b). Пусть также f(a)=f(b). Тогда на интервале (a, b) найдется точка такая, что f ’ ( )=0.

Доказательство. Так как функция y=f(x) непрерывна на [a, b], то она достигает на этом же отрезке наибольшего и наименьшего значений (вторая теорема Вейерштрасса из п.39), т.е. существуют точки x1, x2 [a, b] такие, что f (x1)=min f(x)=m, x [a, b] и f(x2)=max f(x)=M, x [a, b]

Далее выделим два случая.

1. если m=M, то f(x)=m=M=const и поэтому f ’(x)=0, x (a, b);

2. если m<M, то хотя бы одно их двух значений – m или M достигается во внутренней точке отрезка [a, b] (напомним, что значения функции на концах отрезка совпадают). Но тогда в этой точке имеется локальный экстремум и, следовательно, f ’( )=0 по теореме Ферма.

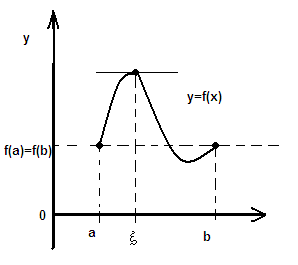
Теорема Ролля имеет довольно простой геометрический смысл: если f(x) удовлетворяет условиям теоремы, то на интервале (a, b) найдется число такое, что касательная к графику функции y=f(x) в точке ( , f ( )) параллельна оси Ox рисунок2.

Рисунок 2.

35 Теорема Лагранжа и Коши для локальных приращений.

Теорема Лагранжа. Формула конечных приращений. Теорема Лагранжа о конечных приращениях является обобщением теоремы Роля.

Теорема Лагранжа. Если функция y=f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b), то на интервале (a, b) найдется точка такая, что справедлива формула:

1. f(b) – f(a)= f ’( )*(b-a).

Доказательство. Рассмотрим на отрезке [a, b] вспомогательную функцию

F(x)=f(x) – f(a) – [(f(b) – f(a))/ b-a] * (x-a).

Легко убедится в том, что функция F(x) удовлетворяет всем условиям теоремы Ролля. В самом деле, F(x) является суммой f(x) и линейной функции и поэтому непрерывна на [a, b] и дифференцируема на (a, b); кроме того, непосредственная проверка показывает, что F(a)=F(b)=0. Итак, по теореме Ролля существует точка (a, b) такая, что F ’( )=0. Но

F’( )=f ’( ) – (f(b) – f(a)) / (b-a), поэтому f ’( ) – (f(b) – f(a)) / (b-a)=0

Или

f(b) – f(a)= f ’( )*(b-a), a< <b.

Теорема доказана.

Формула 1. называется формулой конечных приращений. Смысл такого названия становится очевидным, если в 1. перейти к новым обозначениям. Обозначим b-a= x, -a / -b= (0< <1).

Тогда 1. примет вид:

F(a+ x) – f(a)=f ’(a+ x) x

Или

2. y= f ’(a+ x) x.

Формула 2. связывает приращения функции и ее аргумента и в точке a: приращение функции равно произведению значения производной в точке a+ x (получаемой смещением точки a внутрь отрезка [a, b] на часть его длины, составляющую ) на приращение аргумента.

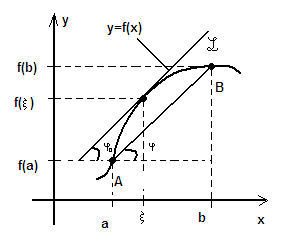
Остановимся также на геометрическом смысле формуле Лагранжа 1. рисунок 3 ,которую мы перепишем в виде f ’( )=(f(b) – f(a)) / (b-a). Значение производной f ’( ) есть не что иное, как тангенс угла, ₀, который составляет касательная к графику функции f(x) с осью Ox. Дробь (f(b) – f(a)) / (b-a), как видно из рисунка, - это тангенс угла наклона хорды, проведенной через точки (a, f(a)) и (b, f(b)) к оси Ox. В теореме Лагранжа утверждается, что y=f(x) в точке параллельна хорде. Это и есть геометрический смысл формулы Лагранжа.

Рисунок3

Теорема Коши (обобщенная формула конечных приращений).

Теорема Коши. Если каждая из двух функций f(x) и g(x) не прерывна на отрезке [a, b] и дифференцируема во всех внутренних точках этого отрезка и если, кроме того, производная g ’(x) отлична от нуля всюду внутри сегмента [a, b], то внутри этого сегмента найдется точка такая, что справедлива формула

3. (f(b) – f(a)) / (g(b) – g(a)) = f ’( ) / g ’( )

(обобщенная формула конечных приращений, или формула Коши).

Доказательство. Докажем сначала, что g(a) g(b). Если бы было g(a)=g(b), то по теореме Ролля нашлась бы точка n (a, b) такая, что в ней g ’(n) =0. Но это противоречит условию теоремы g ’(x) 0. Итак, g(a) g(b).

Теперь рассмотрим функцию

F(x)= f(x)- f(a)- (f(b) – f(a)) / (g(b) – g(a))*[g(x) – g(a)].

Для F(x) выполнены все условия теоремы Ролля, поэтому на (a, b) найдется точка , в которой F ’( )=0, или, если вычислить F ’,

f ’( ) – (f(b) – f(a)) / (g(b) – g(a))*g ’( )=0.

Откуда (g ’=0).

(f(b) – f(a)) / (g(b) – g(a)) = f ’( ) / g ’( ).

Замечание1. Формула Лагранжа является следствием формулы Коши, если положить g(x)=x.

Замечание2. В формуле Коши 3. вовсе необязательно считать, что b>a.