11. Бесконечно малые и бесконечно большие последовательности.
Последовательность
называют
бесконечно малой (б.м), если она имеет
предел, равный нулю. Примеры бесконечно
малых последовательностей:
,
,
.
На
логическом языке
Бесконечно малые последовательности обладают следующим свойством.
Теорема 1. Произведение бесконечно малой последовательности на ограниченную есть бесконечно малая последовательность.
Доказательство.
Пусть
,
-
ограничена :
(константу
с, очевидно, можно считать > 0). Нам
нужно доказать, что
.
Выберем
произвольное
,
тогда в силу сходимости
для
числа
найдется номер N
, начиная с которого выполнено неравенство
.
Но тогда для
получаем
,
Т.е.
.
Среди
расходящихся последовательностей
выделяют особый класс последовательностей
- бесконечно большие (б.б). Определение
их таково: последовательность
называют бесконечно большой, если каково
бы ни было число Е>0, найдется номер N,
начиная с которого все элементы
последовательности удовлетворяют
неравенству
.
Таким образом, как бы ни был велик интервал (-Е, Е) , все элементы бесконечно большой последовательности, начиная с некоторого номера лежат вне этого интервала.
Теорема
2.
Последовательность, обратная бесконечно
большой, является бесконечно малой(если
-б.б
и
,
то
-б.м).
Доказательство.
Последовательность
-б.б
, следовательно,
:
,
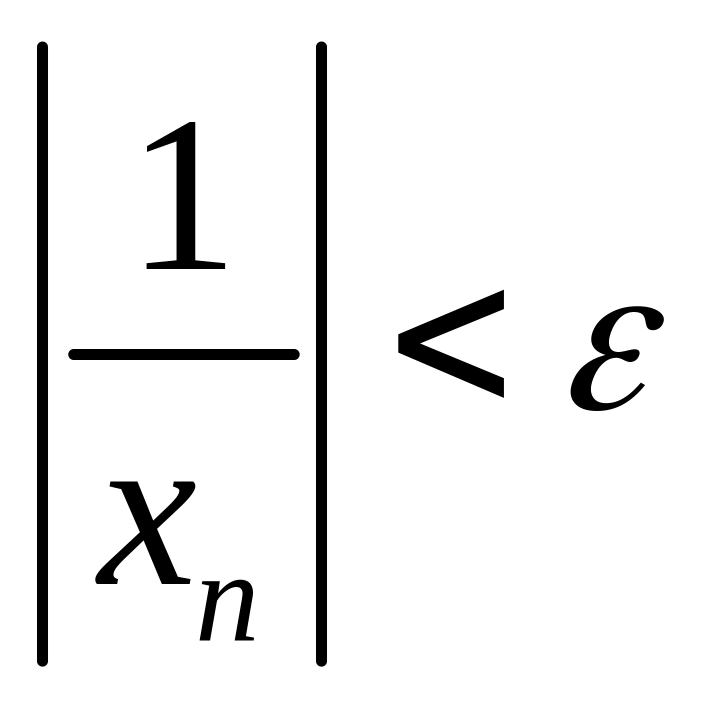А это означает что -б.м последовательность.
Теорема 3. Если бесконечно малая последовательность не содержит нулевых элементов, то обратная ей последовательность является бесконечно большой.
12. Монотонные последовательности. Теорема о пределе монотонной ограниченной последовательности.
Монотонная
последовательность — последовательность
,
удовлетворяющая одному из следующих
условий:
для
любого номера n=1,2...
выполняется неравенство
(убывающая последовательность),
для
любого номера n=1,2...
выполняется неравенство
(возрастающая последовательность).
Среди монотонных последовательностей выделяются строго монотонные последовательности, удовлетворяющие одному из следующих условий:
для любого номера n=1,2... выполняется неравенство X(n + 1) > Xn (строго возрастающая последовательность);
для любого номера n=1,2... выполняется неравенство X(n + 1) < Xn (строго убывающая последовательность).
Теорема Вейерштрасса о пределе монотонной ограниченной последовательности.
Всякая возрастающая числовая последовательность {Xn} имеет предел: конечный, если она ограничена сверху и бесконечный, если она неограниченна сверху, причём lim Xn = sup {Xn} (x>>бесконечность)
Аналогично если {Xn} – убывающая последовательность, то сущ-ут конечный или бесконечный предел lim Xn = inf {Xn} (x>>бесконечность)
И следовательно этот предел конечен, если последовательность {Xn} ограничена снизу, и бесконечен, если она неограниченна снизу
Последовательность
=
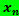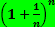и предел 
.
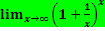Теорема: Последовательность xn=(1+1/n)n сходится. Док-во:
xn = (1+1/n)n = 1+ n/1 * 1/n + n(n-1)/2! * 1/n2 + ... + (n(n-1)(n-2)...(n(n-1)))/n! * 1/nn = 2 + 1/2! * (1-1/n) + 1/3! *(1-1/n)(1-2/n)+ ... + 1/n!*(1-1/n) * (1-2/n) + ... + (1- n-1/n).
Так же поступим с xn+1=(1+1/n+1)n+1 . xn+1 = 2 + 1/2! *(1-1/n+1) + 1/3! *(1-1/n+1)(1-2/n+1)+ ... + (1/(n+1)!) *(1-1/n+1)(1-2/n+1) * ... * (1- n/n+1).
Убеждаемся что xn<xn+1 . Доказываем что xn ограничено сверху, а т.к. существует ограничение, то последовательность сходится.
Предел lim (1+1/x)x существует и равен натуральному числу e.