1.2. Теоремы сложения и

умножения вероятностей

Теоремы сложения и умножения вероятностей являются основными, так как на них основываются все дальнейшие положения теории вероятностей. Указанные теоремы позволяют по вероятностям одних событий вычислять вероятности других. В следствии этого они часто применяются для решения различных задач. Следует усвоить методику использования теорем при решении задач.

Суммой событий и называется событие, заключающееся в том, что произошло хотя бы одно из событий и , а произведением этих событий — событие, состоящее в том, что произошли оба данных события.

Вероятность суммы двух событий можно найти по теореме сложения вероятностей:

Если события и несовместны, то есть не могут произойти одновременно, то вероятность их произведения равна нулю, и теорема сложения приобретает более простой вид:

Вероятность произведения событий определяется по теореме умножения вероятностей:

где — так называемая условная вероятность события , то есть вероятность при условии, что произошло. Если осуществление события не изменяет вероятности события , то и называются независимыми, и вероятность их произведения равна произведению вероятностей сомножителей:

Заметим, что при решении задач теоремы сложения и умножения обычно используются совместно.

Примеры.

1. В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар а) синий или черный; б) белый, черный или синий.

Обозначим следующие события:

Б – вынули белый шар, ;

Ч – вынули черный шар, ;

С – вынули синий шар, ;

К – вынули красный шар, .

Тогда искомые вероятности будут:

а) .

б)

или . ◄

2. На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в переплете. Библиотекарь берет три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

Рассмотрим два способа решения задачи.

Первый способ. Пусть события А – хотя бы один учебник в переплете;

В – один из взятых учебников в переплете, два – без переплета;

С – два в переплете, один без переплета;

D – все три учебника в переплете.

Очевидно, А=В+С+D. Найдем вероятности событий В, С, и D.

, , .

Тогда

.

Второй способ. Вновь А – хотя бы один учебник в переплете;

- ни один из взятых учебников не имеет переплета.

Так как события А и противоположные, то

. ◄

3. Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания равны соответственно 0,6 и 0,9. Найти вероятности следующих событий:

— оба попали в цель;

— в цель попал хотя бы один.

Назовем событиями и попадание в мишень соответственно первого и второго стрелка и отметим, что и являются событиями совместными, но независимыми (иными словами, в мишень могут попасть оба стрелка, а вероятность попадания каждого не зависит от результата другого). Событие представляет собой произведение событий и поэтому

Событие является суммой и для определения его вероятности воспользуемся общим видом теоремы сложения:

◄

4. В первом ящике 2 белых и 7 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Обозначим события: А – вынули белый шар из первого ящика, ;

- вынули черный шар из первого ящика, ;

В – белый шар из второго ящика, ;

- черный шар из второго ящика, .

Нам нужно, чтобы произошло одно из событий или . По теореме об умножении вероятностей , . Тогда искомая вероятность по теореме сложения будет

. ◄

5. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха; в) хотя бы одного попадания; г) одного попадания.

Пусть А – попадание первого стрелка, Р(А)=0,8; В – попадание второго стрелка, Р(В)=0,9. Тогда - промах первого, ; - промах второго, . Найдем нужные вероятности.

а) АВ – двойное попадание, Р(АВ)=Р(А)Р(В)=0,72.

б) - двойной промах, .

в) А+В – хотя бы одно попадание,

.

г) - одно попадание,

. ◄

6. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

=0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8=0,188.

2. .

3. P(АВС)=0,6·0,7·0,8=0,336. ◄

7. Из 10 деталей 7 – стандартные. Наудачу берут 6 деталей. Найти вероятность того, что среди них: а) не более одной нестандартной; б) не более двух нестандартных.

а) Обозначим события А – среди взятых 6 деталей нестандартных нет;

В – в 6 выбранных деталях одна нестандартная. Тогда А+В – среди 6 деталей не более одной нестандартной. Найдем Р(А+В). Заметим, что

,

.

Откуда

.

б) Пусть теперь событие А – в шести взятых деталях не более двух нестандартных. Тогда - в выбранных деталях более двух нестандартных, т.е. три.

.

. ◄

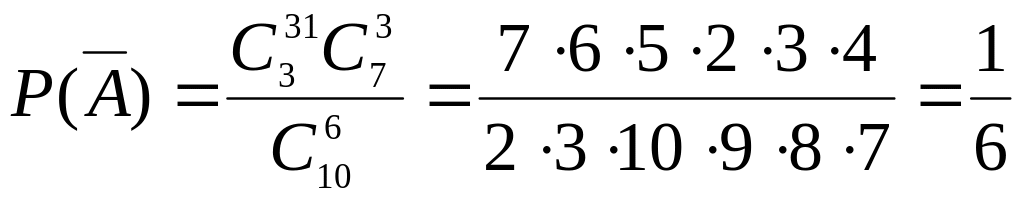8. Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки?

1-й способ. Рассмотрим события: - появление шестерки на первой кости ( ); - появление шестерки на второй кости ( ). События и - совместны и независимы, следовательно,

.

2-й способ. Рассмотрим противоположные события: и . Из свойств вероятности и алгебры событий следует

.

Следовательно,

. ◄

9. В классе 32 ученика.12 из них носят очки. У 10 – пятерка по русскому языку, из них пятеро носит очки. Определить зависит ли между собой события: ученик носит очки и у ученика пятерка по поведению.

Пусть событие ={ученик носит очки}, событие ={у ученика пятерка по русскому языку}.

Тогда .

Так как , то эти события не независимы. ◄