32. Электрические свойства твердых тел: электропроводность металлов.

По величине электропроводности все твердые тела можно разделить на металлы, диэлектрики и полупроводники.

Металлы – проводники электрического тока, удельная электропроводность .

Диэлектрики – используются в качестве изоляторов, .

Полупроводники – твердые тела, имеющие удельную электропроводность .

Одно и то же твердое тело в зависимости от содержания примесей и дефектов может иметь различную электропроводность.

Для полупроводников и диэлектриков с .

Для металлов наоборот, с .

При температуре вблизи абсолютного нуля перестает изменяться, диэлектриков и п/п равна нулю при температуре абсолютного нуля.

Электропроводность металлов можно выразить соотношением

.

3 3. Собственная проводимость полупроводников. Проводимость примесных полупроводников.

Рассмотрим, п/п не содержащий примесей и дефектов.

При T=0 К электропроводность такого полупроводника равна нулю, по­скольку в нем нет свободных носителей заряда. Действительно, валентная зона полностью заполнена электронами и не дает никакого вклада в проводимость, а зона проводимости пуста. При T>0 К появляется вероятность заброса элект­ронов из валентной зоны в зону прово­димости (рис. 8.3). В валентной зоне при этом образуются дырки. Ясно, что концентрация электронов п будет равна концентрации дырок р:

п=р.

Одновременно с процессом образования свободных носителей (генерацией) идет процесс их исчезновения (рекомбинации). Часть электронов возвращается из зоны проводимости в ва­лентную зону и заполняет разорванные связи (дырки). При данной температуре за счет действия двух конкурирующих процессов генерации и рекомбинации в полупроводнике уста­навливается некоторая равновесная концентрация носителей заряда. Так, например, при комнатной температуре концентрация свободных электронов и дырок составляет в кремнии при­мерно 10¹⁰ см^-3, в германии приблизительно 10¹³ см^-3.

Если к полупроводнику приложить электрическое поле , то в нем возникает ток, складывающийся из электронной и дыроч­ной составляющих. Полупроводники, в которых за счет пере­хода некоторого количества электронов из валентной зоны в зону проводимости образуется такое же количество дырок, на­зывают собственными. Соответственно их проводимость, состоя­щую из электронной и дырочной составляющих, называют соб­ственной проводимостью.

Приписав электронам в зоне проводимости и дыркам в ва­лентной зоне эффективную массу, мы можем считать их сво­бодными и воспользоваться выражением для электропроводно­сти.

,

.

При этом

.

Здесь - эффективная масса электрона, - время релаксации.

Аналогичные выражения можно написать и для дырочной составляющей. Результирующая электропроводность собственного п/п определяется суммой электронной и дырочной компонент

,

- подвижность дырок. В последнее выражение входят два важнейших параметра - концентрация и подвижность носителей заряда.

Проводимость примесных полупроводников.

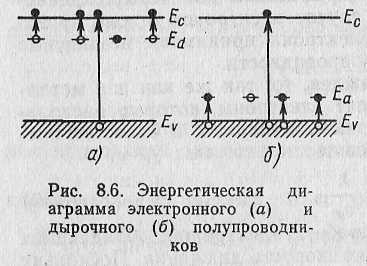Если в полупроводник введена донорная или акцепторная примесь, то при низких температурах, когда энергии тепловых колебаний недостаточно для переброса электронов из валентной зоны в зону проводимости, свободные носители заряда могут появиться за счет ионизации примесных уровней. Энергии ионизации мелких доноров или акцепторов незначительна по сравнению с шириной запрещенной зоны. Поэтому связанный с донорным атомом электрон доста­точно легко может быть оторван от этого атома, т. е. переведен с донорного уровня в зону проводимости (рис. 8.6, а). Чем вы­ше температура, тем больше доноров отдаст свои электроны. С повышением температуры, конечно, увеличивается и вероят­ность межзонных переходов. Однако в данном полупроводнике количество электронов в зоне проводимости будет значительно больше, чем количество дырок в валентной зоне. В силу этого электропроводность полупроводника, содержащего доноры, бу­дет электронной. Электроны являются основными носителями заряда, дырки — неосновными. Такой полупроводник называет­ся электронным (или донорным).

В полупроводнике, содержащем акцепторную примесь электроны легко переходят из валентной зоны на акцептор­ные уровни. При этом в ва­лентной зоне образуются сво­бодные дырки. Количество свободных дырок здесь будет значительно больше, чем ко­личество свободных электронов, образовавшихся за счет переходов из валентной зоны в зону проводимости. Поэтому дырки являются основными но­сителями, а электроны — неосновными. Проводимость полу­проводника, содержащего акцепторную примесь, имеет дыроч­ный характер, а сам полупроводник в соответствии с этим на­зывается дырочным (или акцепторным).

Ясно, что увеличение температуры приведет в конце концов к тому, что все электроны с донорных уровней перейдут в зо­ну проводимости, а дальнейший рост Т вызовет соответствую­щее увеличение концентрации собственных носителей. До тех пор, пока собственной проводимостью можно пренебречь, для электропроводности электронного полупроводника можно на­писать:

,

для дырочного

.

34. Электропроводность диэлектриков.

К диэлектрикам относятся твердые тела, у которых ширина запрещенной зоны превышает 2—3 эВ. Ясно, что при комнатной и более низкой температуре заброс электронов из валентной зоны в зону проводимости практически отсутствует, т. е. концентрация свободных носителей в диэлектрике исключительно мала. Поэтому при указанных условиях, в отличие от узкозонных полупровод­ников, собственная проводимость здесь ничтожна.

В то же время при наличии в диэлектрике примесных ато­мов свободные носители заряда могут появиться за счет терми­ческой активации примесных уровней. Вследествие этого при нормальных и низких температурах проводимость в диэлектри­ках имеет примесный характер. Так же как и в полупроводни­ках, носителями заряда здесь могут быть электроны и дырки. Если примесь имеет донорный характер, то основными носи­телями заряда являются электроны, а неосновными — дырки. Такой диэлектрик (по аналогии с полупроводником) называют электронным, или диэлектриком п-типа. Если же примесь ак­цепторная, то основными носителями будут дырки. В этом случае диэлектрик называют дырочным, или р-типа.

При приложении к диэлектрику электрического поля свободные носители начинают ускоряться и, таким образом, воз­никает электропроводность. В соответствии с природой носителей заряда (электроны или дырки) рассмотренный механизм электропроводности называют в общем случае электронным. Очевидно, что вследствие низкой концентрации электронов (дырок) электропроводность диэлектриков незначительна. Для различных веществ она колеблется от 10^-10 до 10^-22 Ом^-1 см^-1. Необходимо отметить, что механизм генерации может быть не только тепловым. Электроны проводимости в диэлектрике мо­гут появиться за счет облучения светом соответствующей дли­ны волны, быстрыми частицами, вследствие приложения силь­ных полей.

Если электронная проводимость диэлектрика имеет собственный характер, что возможно при повышенных температурах, то, так же как и в случае полупроводников,

.

В случае примесной проводимости вклад в проводимость дает только один сорт но­сителей.

Температурная зависимость электронной проводимости диэлектриков достаточно хорошо описывается выражением

,

где - ширина запрещенной зоны, - постоянная Больцмана.

Эффект Холла.

Явления, которые возникают в твердых тела при совместном действии на них электрического и магнитного полей, называются гальваномагнитными явлениями. Эффект Холла – это явление возникновения в образце с текущем по нему током поперечного эл. поля под действием магнитного.

П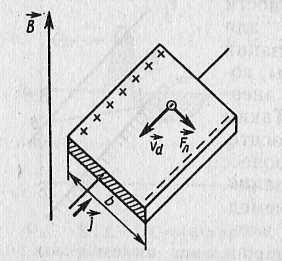 оместим в магнитное поле образец; по нему течет ток ( ). Пусть носителями заряда являются . Они приобретают скорость .

На действует сила Лоренца , и .

В результате траектория электрона будет искривляться. Траектория примет вид циклоиды. Если радиус кривизны траектории много больше длины свободного пробега электрона, то магнитное поле слабое. Пусть магнитное поле слабое.

Под действием силы Лоренца электроны отклоняются к боковой поверхности образца, в результате чего на ней создается избыток отрицательного заряда. На противоположной стороне появится недостаток отрицательного заряда, т. е. избыток положительного. Такое разделение зарядов будет происходит до тех пор, пока сила, действующая на электроны со стороны возникшего эл. поля , направленного от одной боковой поверхности к другой, не скомпенсирует силу Лоренца. Поле получило название поля Холла.

Разделение зарядов прекратится при условии

, т. е. .

Разность потенциалов между боковыми гранями называют э. д. с. Холла. Если ширина образца равна , то

.

Т. к. , где - концентрация, - скорость электронов, то

.

Видно, что пропорциональна и ( ). Коэффициент пропорциональности называется постоянной Холла:

.

Если носителями заряда являются дырки, то для них то же самое. При этом для постоянной Холла имеем

.

Произведение постоянной Холла на проводимость определяет подвижность носителей заряда:

,

которая получила название холловской подвижности.

Измерение эффекта Холла совместно с измерением проводимости образца позволяет получать информацию о знаке носителей заряда, концентрации носителей и их подвижности.

При некоторых условиях холловское сопротивление, равное , становится квантованным и выражается:

,

где , - постоянная Планка.

Измерение квантового эффекта Холла позволяет определить фундаментальную физическую постоянную – отношение .