27.Тепловые свойства твёрдых тел: теплоёмкость твёрдых тел. Закон Дюлонга - Пти.
Если нагревать тело, то поглощаемое тепло будет расходоваться на увеличение интенсивности тепловых колебаний. Основную особенность теплового движения можно понять, если рассмотреть теплоёмкость.
Теплоёмкость вещества, отнесённая к 1 молю - это энергия которую необходимо сообщить телу, чтобы нагреть его на 1 градус.
При изменении температуры:
.
В
1819 году фр. учёные Дюлонг и Пти
экспериментально установили, что при
высоких температурах удельная теплоёмкость
т.т. величина постоянная не зависящая
от температуры и равна
.
Из
закона равновесного распределения
энергии по степеням свободы: средняя
энергия классической системы равна
произведению числа степеней свободы
на
(
- const
Больцмана).
В
качестве классической модели можно
выбрать т.т., атомы которого совершают
колебания вокруг положения равновесия
в узлах кристаллической решётки. Каждый
атом независимо от соседей колеблется
в 3-х взаимно перпендикулярных плоскостях,
т.е. имеет 3 степени свободы (соответствующие
3 гармоническим осцилляторам). При
колебании такого осциллятора кинетическая
энергия переходит в потенциальную и
наоборот. Т.к. кинетическая энергия на
одну степень свободы равна
,
то потенциальная также равна этой же
величине, тогда полная средняя энергия
равна
.
При
наличии для каждого атома 3-х степеней
свободы кристалл представляет собой
степеней свободы.
,
,
где
- молярная газовая const.
.
Эти результаты подтверждены экспериментальными данными для многих т.т. Металл – это совокупность колеблющихся атомов и свободных электронов. Атомы мы представляем как гармонические осцилляторы, а между ними движутся свободные электроны. Каждый электрон обладает 3 степенями свободы.
,
где N – число свободных электронов.
Если
металл одновалентен, то
:
.
Т.о. классическая теория даёт величину теплоёмкости в 1,5 раза больше по сравнению с опытными данными. Физики при объяснении закона Дюлонга – Пти сделали вывод, что электроны не вносят вклад в теплоёмкость металла.
28.Теория теплоёмкости Эйнштейна.
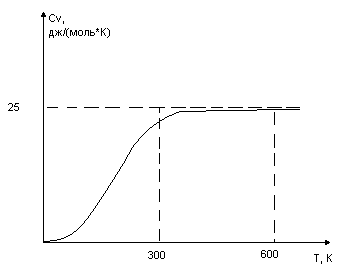
При низких температурах теплоёмкость не постоянна, а увеличивается с увеличением температуры. Для объяснения не достаточно классической физики, а необходимо привлечь квантовую статику.
В 1907 году Эйнштейн предложил модель, которая качественно могла объяснить эту зависимость. Он выходил из квантовой гипотезы Планка.
В 1900 году Планк выдвинул теорию, противоречащую классической физике. Энергия может принимать только дискретные значения:
,
где
- универсальная const
Планка.
В
т.т. энергетические уровни атома образуют
энергетическую лестницу, состоящую из
равноотстоящих ступенек высотой
.
Чтобы объяснить зависимость
Эйнштейн предложил:
1) т.т. – совокупность одинаковых гармонических осцилляторов, которые колеблются независимо друг от друга с одной и той же частотой.
2) энергия осцилляторов квантована по Планку.
Чтобы получить выражение , надо получить выражение тепловой энергии от Т. Такая задача сводится к вычислению средней энергии колебания атома по одному из этих направлений.
,
где n – число атомов,
-
энергия колебания атомов в одном
направлении.
Число
осцилляторов
.
Средняя энергия одного осциллятора:
.
(*).
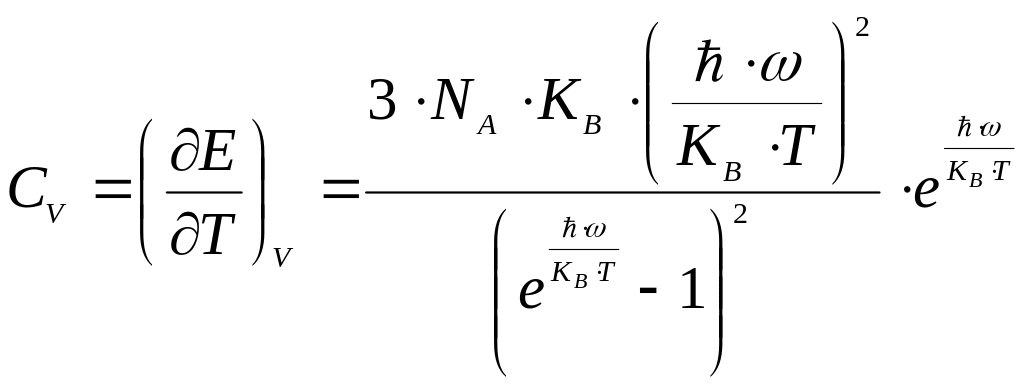1)
При
высоких Т,
.
Полная
энергия
.
2)
При
уменьшении Т,
.
При низких температурах закон равномерного распределения энергии по степеням свободы не справедлив.
Зависимость
средней энергии осциллятора от температуры
при
классическая, 2 – квантовая.
Модель Эйнштейна хорошо описывает факт уменьшения теплоёмкости. Т при которой начинается быстрый спад теплоёмкости называется характерной температурой Эйнштейна.
.
Реальная
температура Эйнштейна зависит от
свойства вещества. Для большинства
.
,
где
- силовая const,
характеризующая силы взаимодействия
между атомами.
М – масса атома.
Чем
жёстче кристалл (чем крепче атомы
«привязаны» к положению равновесия) и
чем меньше масса атомов, тем выше частота
колебаний, а следовательно и выше
температура Эйнштейна.
одна из важных характеристик кристалла.
При
необходимо квантовое рассмотрение
тепловой энергии, при
квантование энергии можно не учитывать.