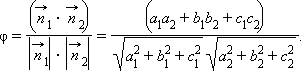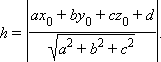1.1.Матрицы: определение, виды матриц.

Линейные операции над матрицами.

Равенство матриц Матрицы  A = || ai j ||  и  B = || ai j ||  считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны: А=В-аij=bij для любых допустимых значений индексов  i  и  j. К линейным операциям над элементами множества или пространства относятся операции сложения элементов и их умножения на скаляр (число). Умножение матрицы на число При умножении матрицы  A  на число  λ  (слева или справа) каждый ее матричный элемент умножается на это число:B= λA-bij=λaij

Сложение матриц Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц  A = || ai j ||  и  B = || bi j ||  является матрица  C = || ci j || , элементы которой равны сумме соответствующих матричных элементов: C=A+B-cij=aij+bijЛинейной комбинацией матриц A и B называется выражение вида αA+ βB Умножение матрицы Умножение матриц (обозначение: AB, реже со знаком умноженияAхB) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть .Свойства арифметических операций над матрицами

Основными арифметическими операциями над матрицами являются умножение матрицы

на число, сложение и умножение матриц.

Сложение матриц: Суммой двух матриц, например: A и B, имеющих

одинаковое количество строк и столбцов, иными словами, одних и тех же порядков

m и n называется матрица С = ( Сij )( i = 1, 2, .m; j

= 1, 2, .n ) тех же порядков m и n, элементы Cij которой равны.

Cij = Aij + Bij ( i = 1, 2, ., m; j = 1, 2, ., n )

Для обозначения суммы двух матриц используется запись C = A + B. Операция

составления суммы матриц называется их сложением

свойствами:

1) переместительным свойством : A + B = B + A

2) сочетательным свойством : (A + B) + C = A + (B + C)

Умножение матрицы на число :

Произведением матрицы A = (Aij) ( i = 1, 2, ., m; j = 1, 2, ., n ) на

вещественное число λ называется матрица C = (Cij) ( i = 1, 2, . , m; j = 1, 2, ., n ), элементы

которой равны Cij = λ Aij ( i = 1, 2, ., m; j = 1, 2, ., n ).

Операция составления произведения матрицы на число называется

умножением матрицы на это число.

Перемножение матриц :

Произведением матрицы A = (Aij) ( i = 1, 2, ., m; j = 1, 2, ., n ), имеющей

порядки соответственно равные m и n,

на матрицу B = (Bij) ( i = 1, 2, ., n;

j = 1, 2, ., p ), имеющую порядки соответственно равные n

и p, называется матрица C = (Сij) ( i = 1, 2, . , m; j =

1, 2, . , p ), имеющая порядки, соответственно равные m и

p, и элементы Cij,

Для обозначения произведения матрицы A на матрицу B используют запись C = AB. Операция составления произведения матрицы A на матрицу B называется перемножением этих матриц. Из

сформулированного выше определения вытекает, что матрицу A можно умножить не на всякую матрицу B : необходимо чтобы число столбцов матрицы A было равно числу строк матрицы B. Для того чтобы оба произведения AB и BA не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы A и B были квадратными матрицами одного и того же порядка являющейся произведением матрицы A на матрицу B.

свойства произведения матрицы A на матрицу B :

1) сочетательное свойство : (AB) C = A (BC);

2) распределительное относительно суммы матриц свойство : (A + B) C = AC + BC или A (B + C) = AB + AC.

Транспонированная матрицаС каждой матрицей A = (aij) размера mхn связана матрица B = (bij) размера nхm видаbij=aij?i=1,m,J=1,n Такая матрица называется транспонированной матрицей для A и обозначается так AT. Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица A = (aij) размера mхn при этом преобразовании станет матрицей размерностью nхm.

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца. Определитель матрицы А обозначается как: det(A), |А| или Δ(A). Определители второго и третьего порядка. определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали. Свойства определителей.1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером.2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -.

3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k..

СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).

СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же.

СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится.

Миноры и алгебраические дополнения.

Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное/

СВОЙСТВО 9. Определитель

равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.

Иначе говоря, имеют место следующие равенства:

, ,

, ,

, .

Разложение определителя по элементам строки (столбца).

     По элементам i-й строки:

     По элементам j-го столбца:

Определители n-го порядка

Определителем (детерминантом) – го порядка или определителем (детерминантом) квадратной матрицы – го порядка называют алгебраическую сумму всех членов определителя данной матрицы, взятых со своими знаками.

Пусть дана квадратная матрица – го порядка:

.

Определение. Произведение  элементов матрицы А, взятых по одному из каждой строки и каждого столбца называют членом определителя матрицы А.

Обозначение: .

Здесь первый индекс обозначает номер строки, из которой взят элемент, второй индекс , он в свою очередь имеет нижний индекс , обозначает номер столбца, из которой взят элемент и набор вторых индексов образует перестановку   множества .

Т.к. число всех перестановок множества  равно , то существует ровно  членов определителя.

Ортогональные проекции векторов. Движение по любой прямой может быть в двух направлениях. Ориентированной прямой называется прямая, на которой выбрано направление, т.е. одно из направлений считается положительным, а противоположное — отрицательным. Для измерения длин отрезков на прямой задается масштабный отрезок, который принимается за единицу. Ориентированная прямая с заданным масштабным отрезком называется осью. Любой ненулевой вектор , принадлежащий прямой, называется направляющим вектором для данной прямой, поскольку задает на ней ориентацию. Направление вектора принимается за положительное, а направление противоположного вектора — за отрицательное. Кроме того, длину вектора — можно принять за величину масштабного отрезка на этой прямой. Поэтому можно сказать, что любой ненулевой вектор определяет ось — прямую, содержащую этот вектор, задавая на ней направление и масштабный отрезок.

Ортогональной проекцией вектора на ось, задаваемую вектором , называется его проекция на ось вдоль прямой (или вдоль плоскости), перпендикулярной данной оси. Ортогональную проекцию вектора на ось, задаваемую вектором , будем обозначать .

Ортогональную проекцию вектора на прямую[/b] I будем обозначать .

Ортогональную проекцию вектора а на плоскость будем обозначать .

Разность между вектором и его ортогональной проекцией называют ортогональной составляющей:

— — ортогональная составляющая вектора относительно вектора ;

— — ортогональная составляющая вектора относительно прямой ;

— — ортогональная составляющая вектора относительно плоскости .

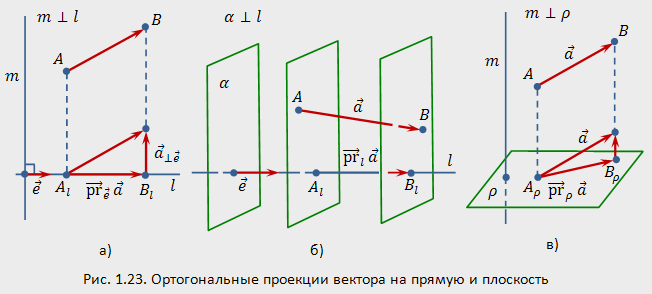
На рис. 1.23 изображены ортогональные проекции вектора :

— на прямую (или на ось , задаваемую вектором ) вдоль прямой (рис.1.23,а);

— на прямую (или на ось , задаваемую вектором ) вдоль плоскости (рис.1.23,б);

— на плоскость вдоль прямой (рис.1.23,в).

На рис. 1.23 изображены ортогональные составляющие вектора :

— относительно оси (вектора ): (рис.1.23,а);

— относительно плоскости (рис.1.23,в).

Теорема об ортогональных проекциях вектора).

1. Если на плоскости заданы две взаимно перпендикулярные прямые и , то любой вектор на плоскости можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е. (рис. 1.24,а).

2. Если в пространстве заданы три попарно перпендикулярные прямые и , пересекающиеся в одной точке, то любой вектор в пространстве можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е. (рис. 1.24,6).

3. Квадрат длины вектора на плоскости или в пространстве равен сумме квадратов длин своих ортогональных проекций, т.е.

Первые два утверждения представляют собой частные случаи теоремы 1.1. Третье утверждение следует из теоремы Пифагора (для треугольника (рис. 1.24,а) или треугольников и (рис. 1.24,6)).

В формулировке теоремы 1.2 прямые можно заменить осями, задаваемыми попарно ортогональными векторами.

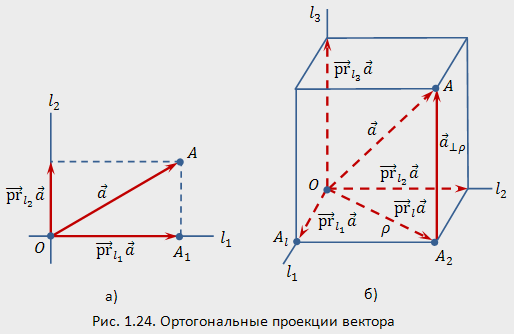
На рис.1.24,а проекции вектора на оси одновременно являются ортогональными составляющими: и . На рис. 1.24,6 вектор является проекцией вектора на плоскость , содержащую прямые и : , а вектор является ортогональной составляющей вектора относительно плоскости .

Свойства проекций.

Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.

Проекция точки есть точка. При заданном центре Р (.или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п' единственная точка А'. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой (см. рис. 43).

Проекция прямой есть прямая. На рис. 46 лучи, проецирующие прямую т, создают плоскость S, которая пересекает плоскость проекций п' по линии m', являющейся проекцией на плоскость n'; S ~ т; S п п = т'. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рис. 49). Если в пространстве прямая параллельна плоскости проекции п', то ее проекция параллельна самой прямой (рис. 50). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.

Рис. 49

При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рис. 51):

АВ/ВС = А'В'/В'С.

При параллельном проецировании проекции параллельных прямых есть прямые параллельные (рис. 52). Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости S^m и Sⁿ тоже будут параллельны. При пересечении их с плоскостью проекций п' получаем т'|| п'.

Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а

Рис. 50

Рис. 51

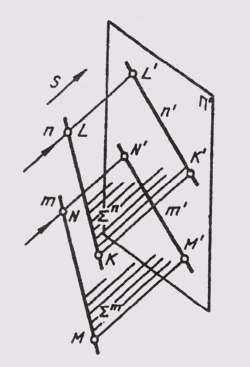
Рис. 52

Рис. 53

их точки пересечения с плоскостью проекций п' — всю плоскость проекций.

Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рис. 53, а) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций n', которое позволяет определить проекции (рис. 53, б) любой точки D или прямой этой плоскости.

Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рис. 54, а), а при параллельном — равны им (рис. 54,6).

Рис. 54

Рис. 55

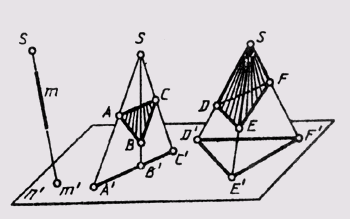
Рис. 56

Рис. 57

Если плоскость угла параллельна плоскости проекций, величина проекции угла и при центральном, и при параллельном проецировании равна натуральной величине. На рис. 54, a угол ABC = уголA'B'C', так как АВС бесконечность А'В'С', а на рис. 54, б угол ABC = углу А'В'С', так как АВС = А'В'С'.

При параллельном проецировании проекции фигуры не изменяется при параллельном переносе плоскости j проекций (рис. 55).

Прямые и плоскости (поверхности) могут занимать в пространстве проецирующее положение, если с ними совпадают проецирующие лучи. При центральном проецировании это прямые и плоскости, проходящие через центр проекций, пирамидальные и конические поверхности, у которых вершины совпадают с центром проецирования (рис. 56). При параллельном проецировании — это прямые и плоскости, параллельные направлению проецирования, призматические и цилиндрические поверхности, ребра и образующие которых параллельны направлению проецирования (рис. 57).

Все эти геометрические фигуры можно рассматривать состоящими из проецирующих лучей, каждый из которых изображается точкой. Отсюда следует, что проекциями прямых, плоскостей, поверхностей, занимающих проецирующее положение, есть точки или линии их пересечения с плоскостью проекций («вырожденные» проекции).

Направляющие косинусы вектора (в пространстве) – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:

где , ,  – углы, составляемые вектором с осями x, y, z соответственно.

Сумма квадратов направляющих косинусов равна 1.

14.

Скалярным произведением двух векторов aиb называется число, равное произведению их модулей на косинус угла между ними. Скалярное произведение векторов aи b обозначается символом ab.Cкалярное произведение двух векторов aи b- это произведение модуля одного из них на проекцию второго на направление первого вектора

откуда .Скалярное произведение двух перпендикулярных векторов равно нулю, Перечислим основные свойства скалярного произведения, которые также доказываются аналогично планиметрическим.

Для любых векторов   и и любого числа λ справедливы равенства:

1. причем

2. (переместительный закон).

3. (распределительный закон).

4. (сочетательный закон).

Признак ортогональности (перпендикулярности) векторов.

Если два вектора перпендикулярны, то косинус угла между ними равен нулю. Поэтому скалярное произведение этих векторов равно нулю. Из этого рассуждения мы получаем следующий признак: два ненулевых вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

Замечание. Если - ненулевой вектор, то вектор перпендикулярен ему и имеет такую же длину.

Скалярное произведение в координатной форме.

Смешанное и векторное произведения векторов в координатной форме.

Теорема. Пусть , , . Тогда:

1) ;

2) .

   Доказательство. 1) Используем свойство линейности векторного произведения:

 

.

   Далее, заметим, что векторные произведения коллинеарных векторов равны нулевому вектору:

                  .

Рассмотрим другие векторные произведения базисных векторов:

                      

                                            рис.4.

, , .

Эти равенства легко устанавливаются с помощью рис.4.

Отсюда следует:

, ч.т.д.

2) Воспользуемся только что доказанной формулой:

        .

Теперь, по теореме о скалярном произведении векторов в координатной форме, получаем:

, ч.т.д.

16. Общее уравнение прямой на плоскости.

Общее уравнение плоскости в декартовой системе координат записывается следующим образом:

ax + by + cz + d = 0.

Если известно, что плоскость проходит через точку с координатами (x₀, y₀, z₀), то ее уравнение можно привести к виду

a (x – x0) + b (y – y0) + c (z – z0) = 0.

Уравнение

называется уравнением плоскости в отрезках на осях.

Нормаль к плоскости имеет координаты

Угол между двумя плоскостями легко вычисляется по формуле скалярного произведения. Если эти плоскости задаются уравнениями a₁x + b₁y + c₁z + d₁ = 0 и a₂x + b₂y + c₂z + d₂ = 0, то угол между плоскостями равняется

Расстояние от точки (x₀; y₀; z₀) до плоскости, задаваемой уравнением ax + by + cz + d = 0, равно

Нормальный вектор и уравнение плоскости в отрезках на осях координат.

Рассмотрим произвольную точку в пространстве и некоторый вектор Очевидно, что геометрическим местом точек таких, что вектор перпендикулярен вектору будет плоскость, проходящая через точку M перпендикулярно прямой, для которой вектор является направляющим. Нашей задачей будет установить уравнение плоскости, то есть найти соотношение, которому удовлетворяют координаты точки A.

Запишем условие перпендикулярности векторов с использованием скалярного произведения:

Запишем последнее равенство в координатах:

Поскольку все наши выкладки были равносильными, то это и есть уравнение плоскости, проходящей через заданную точку. Преобразуем его к виду

Обозначая получим

Это и есть так называемое общее уравнение плоскости.

Вектор называется нормальным вектором (или просто нормалью) для плоскости, заданной общим уравнением (1).

Нормальный вектор к плоскости перпендикулярен ей, что следует из самого вывода уравнения плоскости.

Рассмотрим плоскость 3x + 2y + z – 6 = 0. Пусть A – точка пересечения этой плоскости с осью Ox, то есть A(2; 0; 0). Точка B(0; 3; 0) – это точка пересечения данной плоскости с осью Oy, точка C(0; 0; 6) – с осью Oz (чертеж 9.7.1). Уравнение называется уравнением плоскости в отрезках на осях.

Уравнение плоскости, проходящей через заданную точку.

Положение плоскости в пространстве вполне определяется заданием вектора , перпендикулярного к плоскости

(нормальный вектор), и т. . Найдем уравнение этой плоскости. Пусть т. — точка с текущими координатами. Тогда

17. Уравнение прямой на плоскости

Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно, т.е. А² + В²  0. Это уравнение первого порядка называют общим уравнением прямой.

            В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

-          C = 0, А  0, В  0 – прямая проходит через начало координат

-          А = 0, В  0, С  0 { By + C = 0}- прямая параллельна оси Ох

-          В = 0, А  0, С  0 { Ax + C = 0} – прямая параллельна оси Оу

-          В = С = 0, А  0 – прямая совпадает с осью Оу

-          А = С = 0, В  0 – прямая совпадает с осью Ох 

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Нормальный вектор прямой.

Нормальным вектором прямой называется любой ненулевой вектор, перпендикулярный этой прямой.

Уравнение прямой в отрезках, на осях координат.

Общее уравнение прямой:

 

Ах +  Ву +  С = 0 ,

 

где  А и В  не равны нулю одновременно.

Коэффициенты А и В являются координатами нормального вектора прямой ( т.е. вектора, перпендикулярного прямой ). При  А = 0  прямая параллельна оси ОХ , при  В = 0 прямая параллельна оси ОY .

При  В 0  получаем  уравнение прямой с угловым коэффициентом:

Уравнение прямой, проходящей через точку ( х₀ ,  у ₀ ) и не параллельной оси OY, имеет вид:

 

у – у ₀ = m ( x – х₀ ) ,

 

где  m  –  угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ .

При  А 0,  В 0 и С 0  получаем  уравнение прямой в отрезках на осях:

где  a = – C / A ,   b = – C / B . Эта прямая проходит через точки ( a, 0 ) и ( 0, b ), т.е. отсекает на осях координат отрезки длиной  a  и  b .

18. Параметрическое уравнение прямой, проходящей через точку ( х₀ ,  у ₀ ) и параллельной направляющему вектору прямой ( a, b ) :

Каноническое уравнение прямой

Направляющий вектор

Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.

Направляющий вектор произвольной прямой в дальнейшем обозначается буквой , его координаты - буквами l, m, n:

.

Если известна одна точка прямой и направляющий вектор , то прямая может быть определена (двумя) уравнениями вида

. (1)

В таком виде уравнения прямой называются каноническими.

Канонические уравнения прямой, проходящей через данные точки и имеют вид

. (2)

Обозначим буквой t каждое из равных отношений в канонических уравнениях (1); получим

.

Отсюда

, , . (3)

Это - параметрические уравнения прямой, проходящей через точку в направлении вектора . В уравнениях (3) t рассматривается как произвольно изменяющийся параметр, x, y, z - как функции от t; при изменении t величины x, y, z меняются так, что точка M(x; y; z) движется по данной прямой.

Если параметр t рассматривать как переменное время, а уравнения (3) как уравнения движения точки М, то эти уравнения будут определять прямолинейное и равномерное движение точки М. При t=0 точка М совпадает с точкой . Скорость v точки М постоянная и определяется формулой

Уравнение прямой с угловым коэффициентом

y = kx + b,     (1)

где k - угловой коэффициент прямой, т. е. тангенс того угла, который прямая образует с положительным направлением оси Ox, причем этот угол отсчитывается от оси Ox к прямой против часовой стрелки, b - величина отрезка, отсекаемого прямой на оси ординат. При b = 0 уравнение (1) имеет вид y = kx и соответствующая ему прямая проходит через начало координат.

Уравнением (1) может быть определена любая прямая на плоскости, не перпендикулярная оси Ox.

Уравнение прямой с угловым коэффициентом разрешено относительно текущей координаты y.

Уравнение прямой с угловым коэффициентом через заданную точку

y = y0 + k (x – x0)

называется уравнением прямой с заданным угловым коэффициентом, проходящей через заданную точку.

7. СЛАУ. Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида (1)

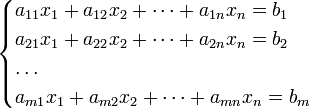
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.

Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой. Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Условия совместности. Условие для всех может быть сформулировано в качестве необходимого и достаточного условия совместности:

Следствия:

Количество главных переменных равно рангу системы и не зависит от её решения.

Если ранг совместной системы равен числу переменных данной системы, то она определена.

Теорема Кронекера-Копелли. Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

RgA = RgA*.

Очевидно, что система (1) может быть записана в виде:

x1 + x2 + … + xn

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.

2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

8. Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы. Метод является модификацией метода Гаусса.

Алгоритм

1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.

2. Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.

3. Все элементы первой строки делят на верхний элемент выбранного столбца.

4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

6. После повторения этой процедуры n − 1 раз получают верхнюю треугольную матрицу

7. Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.

9. Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

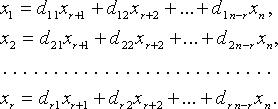
Тогда n - r линейно независимыми вектор-решениями будут:

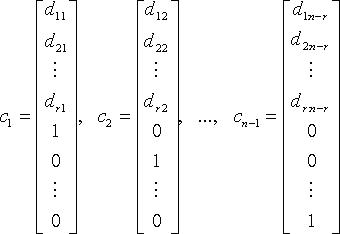
а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.

В линейном пространстве множество решений однородной системы линейных уравнений образует подпространство размерности n – r, - базис этого подпространства.

Фундаментальная система решений. Множество решений однородной линейной системы относительно n неизвестных является линейным подпространством пространства Rn. Размерность этого подпространства равна n − r, где r − ранг матрицы системы A.

Любой базис пространства решений однородной системы линейных уравнений называется фундаментальной системой решений однородной системы.

Иначе говоря, любая упорядоченная совокупность n − r линейно независимых решений однородной линейной системы образует фундаментальную систему решений однородной системы.

10. Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила.

Геометрически векторы изображаются направленными отрезками.

Направленный отрезок называется вектором.

Вектор характеризуется следующими элементами:

1) начальной точкой (точкой приложения);

2 )направлением;

3) длиной («модулем вектора»).

12. Действия над векторами, заданными своими координатами. Если векторы заданы своими координатами в базисе e1, e2 , e3, то действия над ними выполняются по следующим правилам:

1. При сложении двух (или большего числа) векторов их соответственные координаты складываются:

(x1; y1; z1) + (x2; y2; z2) = (x1 + x2; y1 + y2; z1 + z2).

В самом деле, для двух векторов (x1; y1; z1) и (x2; y2; z2) имеем

(x1; y1; z1) + (x2; y2; z2) =

= (x1e1 + y1e2 + z1e3) + (x2e1 + y2e2 + z2e3) =

= (x1 + x2) e1 + ( y1 + y2) e2 + (z1 + z2) e3 =

= (x1 + x2; y1 + y2; z1 + z2).

2. При вычитании векторов их соответственные координаты вычитаются:

(x1; y1; z1) — (x2; y2; z2) = (x1 — x2; y1 — y2; z1 — z2)

3. При умножении вектора на число все его координаты умножаются на это число.

В самом деле, для вектора (x1; y1; z1) и числа λ, имеем

λ (x1; y1; z1) = λ (x1e1 + y1e2 + z1e3) =

= (λ x1)e1+ (λ y1)e2 + (λ z1)e3 = (λx1; λy1; λz1)

Коллинеарность. Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

В координатной форме- Если векторы коллинеарны, то их координаты пропорциональны. Например: Имеем векторы a(x1,y1,z1) и b(x2,y2,z2) Если x1/x2=y1/y2=z1/z2, то векторы коллинеарны.

Деление отрезка в заданном отношении. Если x1 и y1 - координаты точки A, а x2 и y2 - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении = , определяются по формулам

,

Если , то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам

,