6)Теорема о движении твердого тела. Представление сложного движения твердого тела как суммы поступательного и вращательного движений. Вывод момента инерции диска, стержня.

7)Замкнутая система тел. Закон изменения и закон сохранения импульса. Условия сохранения импульса в случае незамкнутой системы тел. Примеры.

Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют.

Зако́н сохране́ния и́мпульса утверждает, что векторная сумма импульсов всех тел замкнутой системы есть величина постоянная. Если сумма всех внешних сил равна нулю (замкнутая система) или внешние силы вообще на нее не действуют (изолированная система), то изменение импульса равно нулю и импульс остается неизменным P = const. 

 

Изменение импульса материальной точки за малый промежуток времени равно элементарному импульсу за тот же промежуток времени результирующей всех сил, действующих на эту материальную точку.

Для системы точек

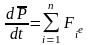
8)Момент импульса материальной точки и твердого тела относительно оси. Закон сохранения момента импульса. Примеры применения закона.

Момент импульса механической системы (точки и тела ибо система это много точек) относительно оси называется проекция на это ось вектора момента импульса системы относительно любой точки, выбранной на оси.

Закон сохранения момента импульса.

Момент импульса замкнутой системы относительно неподвижной точки не изменится с течением времени. (dL/dt)=0 т.е. L=const

Условие выполнения для незамкнутой системы

(dL/dt)=Mвнеш=0 => L=const

Пример Гироскоп:

Момент всех внешних сил будет равен только моменту силы трения.

Момент импульса механической системы относительно неподвижной т О называется вектор L равный геометрической сумме моментов импульса относительно той же точки всех точек системы.

9) Работа как способ передачи энергии. Работа силы и ее выражение через криволинейный интеграл. Кинетическая энергия тела и механической системы тел. Связь кинетической энергии с работой внешних и внутренних сил, приложенных к телу и системе тел.

Работа силы F на малом перемещении dr точки М приложения силы называется скалярное произведение

F на dr

А = F* dr = F*v* dt

A = (1 интеграл 2)F dr

Кинетическая энергия – энергия механического движения этой системы. W = m*v^2 / 2

10) Кинетическая энергия вращающегося тела. Работа, совершаемая внешними силами при вращении тела. Кинетическая энергия тела при сложном движении. Пример.

d W(k) = ½ * V^2* dm = 1/2 * w^2 * p^2 * dm

W(k) = (I* w^2) /2

При вращении точка проходит путь

dS = r* df f-угол фи

dA = F* dS = F* r* df

dA = M* df

w = df/ dt

dA = M* w* dt

W(k) = (m* v^2)/2 + (I* w^2)/2

11)Потенциальные силы и поля. Потенциальная энергия материальной точки и системы материальных точек. Связь между изменением потенциальной энергии и работой силы поля. Пример расчета потенциальной энергии точки и системы материальных точек.

Потенциальные силы - работа которой зависит только от конечного и начального положения или работа по замкнутой траектории равна 0.

Потенциальное поле – не изменяющееся с течением времени поле, действующее на точку с силой F , причем F – потенциальна.

Потенциальная энергия – равна работе, которую совершают действием на систему материальных точек потенциальные силы при переводе системы в состав нулевой конфигурации (пот. Энергия = 0)

dA=Fdr=-dWп (Связь изменения потенциальной энергии и работы)

Расчет потенциальной энергии:

Wп= - Fт*(h) + Wп(0)=mgh

Тело падает с высоты h.

12) Полная механическая энергия системы тел. Связь между изменением полной механической энергии и работой неконсервативных сил. Закон сохранения механической энергии. Примеры применения закона.

Полная механическая энергия – сумма потенциальной и кинетической энергии

W = W(k) + W(p)

Изменение механической энергии системы равно сумме работ непотенциальных сил

ЗСЭ. Механическая энергия неконсервативных сил системы не изменяется с течением времени

Условие: все силы внутренние и внешние непотенциальны не совершают работу

или система замкнута, а все внутренние силы потенциальны

13)Закон изменения и сохранения механической энергии и условия его выполнения. Упругий и неупругий центральный удар.

Упругий удар – в момент удара систему можно считать замкнутой. Т.к. деформация =0 => Wп=const

ЗСЭ: Энергия никуда не девается, она переходит из одного состояния в другой.

ЗСИ: Импульс до взаимодействия равен импульсу после взаимодействия.

Если удар абсолютно неупругий, то после взаимодействия они движутся как единое целое.

14) Идеальный газ. Уравнение Клайперона-Менделеева. Закон Дальтона

Идеальный газ – газ, молекулы которого имеют пренебрежимо малый собственный объем и не взаимодействуют друг с другом на расстоянии

PV = (m/M)* R* T

В смеси газов давление каждого газа такое, каким было бы, если бы он один занимал тот же объем

15) Молекулярно-кинетическая модель идеального газа. Давление газа с молекулярно-кинетической точки зрения. Вывод основного уравнения молекулярно-кинетической теории идеальных газов для давления.

Модель идеального газа на основе Молекулярно –кинетической теории.

-объем частицы газа равен 0

-импульс передается только при соударении

-суммарная энергия частиц постоянна.

PV=(2/3)*Wк

v(кв)=корень(1/N*сумма(u^2))

P=c(m(0))^(альфа)*u^(бетта)*(n(0))^(гамма)

P=c*n(0)*m(0)*u^(2)=2*c*Wк/V

C=1/3 => pv=(2/3)*Wк

16) Основное уравнение молекулярно-кинетической теории идеальных газов для давления и его сравнения с уравнением Клайперона-Менделеева. Средняя квадратичная скорость молекул. Внутренняя энергия одноатомного идеального газа

PV = 2/3 W(k)

PV = (m/M)* R* T => v(кв) = (sqrt(3* R* T))/M = sqrt((3* K* T)/ m(0))

U = 3/2 (m/M)* R* T

17)Число степеней свободы. Закон распределения энергии по степеням свободы молекул. Внутрення энергия идеального газа.

Число степеней свободы называется число, которое необходимо задать для того, чтобы определить положение тела в пространстве.

На каждую степень свободы молекулы в среднем приходится одинаковая химическая энергия равная ½ *k*T

Um = <Wк>Na=(i/2)*k*T*Na=(i/2)*(m/M)*R*T

18) Внутренняя энергия идеального газа. Работа газа при расширении. Количество теплоты. Первое начало термодинамики. Уравнение Пуассона для адиабатного процесса.

При расширении газ совершает работу эта работа А > 0

A =(1 интеграл 2) P dV

Внутренняя энергия – это сумма энергий молекулярных взаимодействий и тепловых движений молекул

дельтаU = дельтаQ – дельтаА

Количество теплоты – энергия, которую получает или теряет тело при теплопередаче

Q = A + дельтаU

Теплота, сообщаемая системе расходуется на изменение внутренней энергии системы и на совершение работы против внешних сил

PV(1)^(гамма) = PV(2)^(гамма)

Гамма = (i+2)/i

19)Применение первого начал термодинамики к изобарному и изохорному процессам. Теплоемкость тела, удельная и молярная теплоемкости. Молярная теплоемкость при постоянном давлении и при постоянном объеме.

Теплоемкость тела – физическая величина, которая равна отношению теплоты , сообщаемой телу к изменению температуры.

C=Q/dT

Молярная теплоемкость- физическая величина С, числено равная теплоте, которую нужно сообщить одному молю вещества для изменения его Т на 1К.

Сv=Mc=(M/m)*(Q/dT) удельная теплоемкость ,

Удельная теплоемкость – кол-во энергии, необходимое для нагревания одного килограмма вещества на 1 градус.

dU=dQ

dU=(m/M) *Cv*dT т.к. в изохорном процессе А=0

Сv-молярная теплоемкость при постоянном объеме

dQ=(m/M)*Cp*dT

20) Работа газа. Количество теплоты. Внутренняя энергия системы. Первое начало термодинамики для изотермического процесса. Сравнение работы газа при изотермическом и адиабатном процессах. Политропные процессы. Работа газа при политропном процессе.

Для изотермического процесса:

dU = 0, так как Т = const

A(1-2) = (v1 интеграл v2) P* dV = (m/M)* R* T *(v1 интеграл v2)(dV/V) = (m/M)* R* T* ln(V(2)/V(1))

Теплоемкость газа при изотермическом процессе стремится к бесконечности

Адиабатный процесс:

dA = -dU

dU = (m/M)* c(v)* (T(1) – T(2))

dA = -(m/M)* c(v)* dT

c(v) = (R/(гамма – 1))

с(ад) = 0 (dQ/ dT)

поэтому

A = ((P(1)* V(1)) / (гамма - 1))* [1 – (T(2)/T(1)]

Политропный процесс – термодинамический процесс описываемый уравнением:

P* V^(гамма) = const

1) n = 0

с = с(p)

2) n = 1

c = c(t)

3) n = гамма

c(ад) = 0

4) n = +- беск

c(v) = (R/(гамма -1))

A(1-2) = ((P(1)*V(1))/(n-1))* [1 – (V(1)/V(2))^(n-1)]