- •3. Свойства действительных чисел. Важнейшие подмножества .
- •4. Ограниченные и неограниченные числовые множества. Грани числовых мно-
- •5. Предел числовой последовательности.
- •6. Свойства предела числовой последовательности.
- •7. Предел последовательности и неравенства.
- •9. Предельный переход и арифметические операции над последовательностями.
- •10. Монотонные последовательности. Число е.
- •11.Сравнение асимптотического поведения последовательностей
- •13.Лемма о вложенных отрезках.
- •14.Фундаментальные последовательности.
- •15.Нижний и верхний пределы последовательности.
- •16. Отображения и их основные типы. Функция действительной переменной.
- •17. Основные классы функций.
- •18. Предел функции. Определения Гейне и Коши.
- •19. Односторонние пределы. Эквивалентность определений предела Гейне и Коши.
- •20. Общие свойства предела функции. Арифметические операции и предельный пе-реход. Предельный переход и неравенства.
- •21. Бесконечно малые и бесконечно большие функции.
- •26. Критерий Коши для функций.
- •27. Непрерывность функции. Точки разрыва и их классификация. Односторонняя и кусочная непрерывность.
- •28.Локальные свойства непрерывных функций.
- •29.Глобальные свойства непрерывных функций. Теорема Больцано-Коши.
- •30.Глобальные свойства непрерывных функций. Теоремы Вейерштрасса.
- •31) Теорема о существовании и непрерывности обратной функции
- •32) Равномерная непрерывность. Теорема кантора
- •33) Непрерывность элементарных функций
- •34. Дифференцируемые функции. Определение производной функции в точке. Условия дифференцируемости функции в точке.
- •36. Односторонние и бесконечные производные.
- •43.Производные и дифференциалы высших порядков. Формула Лейбница. Неинва-
- •44. Локальная формула Тейлора. Единственность многочлена Тейлора.
- •45. Представление остаточного члена в формуле Тейлора в формах Лагранжа и Коши.
- •46. Разложение по ф-ле Маклорона важн элемент ф-ий
- •47. Многочлен Тейлора как многочлен наилучшего приближения функции в окрестности данной точки.
- •50 Выпуклость графиков функции.
- •51. Точки перегиба.
- •52 Асимптоты графика функции.
- •52(Продолжение)
26. Критерий Коши для функций.

df: Колебанием фун-ии f:X->R наз.величина
ω(f,x)=
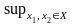 {|
{|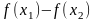 |}
|}
Критерий Коши в терминах колебаний:

27. Непрерывность функции. Точки разрыва и их классификация. Односторонняя и кусочная непрерывность.
ОП. Непрерывность ф-ции.
Ф-ция f:X->R по мн-ву Х наз. непрерывной
в т. а из Х, если в этой точке она имеет конечн.
предел равный f(a), т.е. сущ. limf(x)=f(a), x->a.
ОП. В терминах Эпс-дельта.
Для любого Эпс>0 сущ дельта>0 | для всех х из
Х: |x-a|<дельта => |f(x)-f(a)|<Эпс.
ОП. В терм. окрестностей.
Для любой окрестн. V(f(a)) сущ. окрест. U(a):
f(пересеч. U(a) и Х) принадлежит V(f(a))
ОП. В терм. приращений.
Ф-ция непрерывна в точке, если бесконечно
малое приращение аргумента в точке соотв.
бесконечно малому приращ. ф-ции в точке.
1)Устранимая точка разрыва – если пределы
справа и слева равны. (x->a+0 , x->a-0)
2)Точка разрыва 1 рода если пределы слева
и справа конечные, но не равны.
3) Точка разрыва 2 рода, если хотя бы 1
предел не существует или бесконечный.
ОП. Скачок функции: дельта f=f(a+0)-f(a-0)
28.Локальные свойства непрерывных функций.
Опр. Локальными называются такие свойства функций, которые определяют поведение функций в сколь угодно малой окружности.
Основные локальные свойства:
Th1 f:Х R непрерывна в т.а
Тогда:
а) f ограничена в некоторой И(a)
б)
если f(а) 0,то
существует И(a),
что на множестве И(a)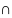 (х),
f(х) принимает значения того же знака
что и f(а).
(х),
f(х) принимает значения того же знака
что и f(а).
в)пусть даны f:Х R непрерывна в точке а
g:Х R непрерывна в точке а
Тогда
существует И(a)
такая, что
на И(a)
х определено частное
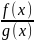
Доказательство:
а) вытекает из ограниченной функции имеющей конечный предел
б)т.к.
f(а) 0,
то можно выбрать
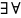 (
f(а))
/0.
Тогда
(
f(а))
/0.
Тогда
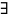 И(a): f(И(a)
(х))<
V(f(а))
И(a): f(И(a)
(х))<
V(f(а))
И(a)-искомая
в)для того чтобы частное надо чтобы g(а) 0
Th2 Если f(x), g(x) - непрерывны в точке a, то функции: f(x)+g(x), f(x)g(x), f(x)/g(x) (при g(a)№ 0 ) непрерывны в точке a.
Доказательство: Утверждение вытекает из свойств предела арифметической комбинации функции.
Th3 (о непрерывной композиции)
Функция f:Х Y непрерывна в точке a Х, а функция g:Y R непрерывна в точке b Y, f(a) = b, тогда композиция g° f:Y R также непрерывна в точке a.
29.Глобальные свойства непрерывных функций. Теорема Больцано-Коши.
Теорема Больцано-Коши – с доказательством.
Th1 (теорема Больцано-Коши о существовании корня непрерывной функции)
Пусть функция f непрерывна на отрезке [a,b] и принимает на концах отрезков значения разных знаков f(a)f(b)<0, то существует c [a,b] f(c) =0
Доказательство:
d=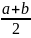 ,если
f(d)=0
, то искомая точка найдена ,если же f(d)
0
, то [a,d]
[d,b]
на концах
отрезков функция принимает значение
разных знаков . Этот отрезок обозначается
[a,b] .
Отрезок [a,b]
снова разделим
пополам такой d
и тд.
,если
f(d)=0
, то искомая точка найдена ,если же f(d)
0
, то [a,d]
[d,b]
на концах
отрезков функция принимает значение
разных знаков . Этот отрезок обозначается
[a,b] .
Отрезок [a,b]
снова разделим
пополам такой d
и тд.
f(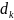 )=0
и искомая точка найдена, либо во всех
точках f(
)
0
и мы получаем бесконечную последовательность
вложенных отрезков,длины которых
)=0
и искомая точка найдена, либо во всех
точках f(
)
0
и мы получаем бесконечную последовательность
вложенных отрезков,длины которых
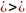 0.
0.
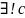 limn
limn 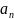 =
limn
=
limn 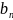
[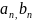 ]
f(
)
* f(
)<0
]
f(
)
* f(
)<0
f(c)* f(c) 0