9. Предельный переход и арифметические операции над последовательностями.

Теорема. Предел суммы или произведения послед-тей равен сумме или произведению их пределов.

Лемма. Если lim(Yn)=b и не равен нулю, то начиная с некоторого номера определена послед-ть, которая явл. ограниченной.

Теорема. Пусть сущ. Lim(Xn)=a при n->+беск. и lim(Yn)=b при n->+беск. при чем Yn не равно нулю для всех n, тогда послед-ть (Xn / Yn) сходится и предел частного равен частному пределов.

10. Монотонные последовательности. Число е.

13) Теорема. Любая монотонная послед-ть имеет

конечн. или бесконечн. предел. Если послед-ть

ограничена, то ее предел конечный.

Для неогранич послед – предел (+/- беск)

(возрастающая/убывающая)

Число е) Послед-ть Xn = (1+1/n)ⁿ – сходится.

и равна числу e( экспонента)

е = 2,718281828459045…

e – иррациональное число

у=х в степени е обознач . “у=expx”.

11.Сравнение асимптотического поведения последовательностей

Нахождение некоторых пределов.

Теорема. Справедливы утверждения:

А)Если α > 0,то = 0

B) fix α , |α|>1, то = 0

С) =1

D) fix α >0 =1

E) fix α >0 ,a ,α >0 = 0

F) ) fix α = 0

Доказательство пункта «a» :

= 0.

- 0| <E   >  >

+1.

Доказательство пункта «b» :

fix α , |α|>1, то = 0

0<| | = a>1

Если a <-1….

Рассмотрим частный случай когда альфа =1

= 0 ????

По биному Ньютона …….{да ну нах стока писать, все его и так знают}

Пусть альфа принадлежит множеству действительных чисел- произвольное.

Пусть m принадлежит множеству натуральных чисел и больше чем альфа(например m= [a]+1).

a < < = (*) ,где b= - фиксир. Число (b>1)

Выше доказано, что = 0. =

(*) : 0< < тогда по теореме о сжатой переменной следует = 0

12. «О»– символика.

Для сравнения роста и убывания последовательностей при n->бесконечности ,используются специальные символы :

«о» - “о” малое

«О» - “о” большое

« » - “о” большое со звёздочкой

~ - эквивалентность

Эти символы составляют “о” символику.

Опр. Для и принято использовать запись ,что для всех номеров. В частности

означает что ( ).

1.  =0

2. о( )  < E| |

Опр. Пусть и -бмп.Тогда называется бесконечно малой более высокого порядка, по сравнению с , если ,при .

Опр. при если существует ограниченная ( ),такая что ,

Замечание. Если {тут короче ребята непонятно нихера}

Другие формы записи

1) ( ) – огр. Последовательность

2) о( ) n  М| | ,

Опр.Если для и 0, то .

Замечание. Если при n -> бесконечности, то при n -> бесконечности. Обратное неверно

Опр.Если для некоторого p>0, при n -> бесконечности, то говорят, что является б.м. порядка p относительно .

Опр. и являются эквивалентными последовательностями при n -> бесконечности, если =1. ~ , при n -> бесконечности.

Замечание.( ~ ) => ( ).Обратное неверно.

13.Лемма о вложенных отрезках.

Пусть задана последовательность вложенных отрезках [ a_n , b_n ], длины которых , т.е:

1. [ a₁ , b₁ ] ɔ [ a₂ , b₂ ] ɔ … ɔ [ a_n , b_n ] … (1)

2. 

тогда Ǝ! Точка c, которая всем отрезкам ∀ n єN c є [ a_n , b_n ]

с

a₁

a₂

a₃

b₁

b₂

b₃

◄ ∀ n, k є N : [ a_n+k , b_n+k ] Ϲ [ a_n , b_n ] =>

=> a_n+k ≥ a_n => (a_n) b_n+k ≤ b_n => (b_n)

∀ n a_n ≤ b_n , b_n ≥ a_n => a_n - ограничена сверху, b_n - ограничена снизу

по теореме о монотонной последовательности:

Ǝ , Ǝ ; a_n ≤ a_n+k ≤ b_n+k ≤ b_n

a_n ≤ a ≤ b ≤ b_n

0 ≤ b-a ≤ b_n - a_n

по условию теоремы b_n - a_n 0 b-a = 0 => b=a => c=b=a Ǝ! C | [ a_n , b_n ] = {c}►

Подпоследовательности.

Пусть есть некот. числ. послед. (x₁ ,x₂ ,x₃ , … ,x_n , …). Пусть есть ещё одна послед. (n₁ < n₂ < n₃ < … < n_k < …) возрастающих натуральных чисел, тогда послед. (Xn₁ ,Xn₂ ,Xn₃ , … ,Xn_k , …) называется подпоследов. послед. 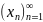и обозн.

Принцип выбора в R.

Из ∀ огран. послед. Можно выделить сход. подпослед.

◄Пусть есть - ограниченная

1. Члены последовательности принимают лишь конечное разных значений. Тогда хоть одно из этих значений принимается число раз. Рассмо трим пример “с”. Тогда (с, с, с, ...) – подпоследовательность {x_n}, сходящаяся к c.

2. Послед. принимает число разных значений, т.к. - огранич., то Ǝ [a , b] : ∀ nєN. Применим метод половинного ÷ x_n ϵ [a , b]. Разделим [a , b] на 2-е равные части, тогда хотя бы одна из этих частей должна содержать число членов послед. Обозн. её [a₁ , b₁]. Длина этого отр. = . [a₁ , b₁] снова разделим на 2-е части. Опять хотя бы одна из них из них сод. число членов послед [a₂ , b₂]= … [a_k , b_k]= . Получим послед. вложен. отрезков:

Ǝ c = на [a₁ , b₁] ∀ член. послед. Пусть это будет [a₂ , b₂] содержит число членов послед. => из них можно выбрать такой чл. послед, что n₂ ≥ n₁ [a₃ , b₃] n₃> n₂> n_1. [a_k , b_k] n_k> … >n₃

a₁< <b₁

a₂< <b₂

_…

a_k< <b_k

т.к. , то Ǝ . - искомая форма члена►

Принцип выбора в .

Из ∀ послед. Можно выделить сход. в подпоследовательность.