
- •3. Свойства действительных чисел. Важнейшие подмножества .
- •4. Ограниченные и неограниченные числовые множества. Грани числовых мно-
- •5. Предел числовой последовательности.
- •6. Свойства предела числовой последовательности.
- •7. Предел последовательности и неравенства.
- •9. Предельный переход и арифметические операции над последовательностями.
- •10. Монотонные последовательности. Число е.
- •11.Сравнение асимптотического поведения последовательностей
- •13.Лемма о вложенных отрезках.
- •14.Фундаментальные последовательности.
- •15.Нижний и верхний пределы последовательности.
- •16. Отображения и их основные типы. Функция действительной переменной.
- •17. Основные классы функций.
- •18. Предел функции. Определения Гейне и Коши.
- •19. Односторонние пределы. Эквивалентность определений предела Гейне и Коши.
- •20. Общие свойства предела функции. Арифметические операции и предельный пе-реход. Предельный переход и неравенства.
- •21. Бесконечно малые и бесконечно большие функции.
- •26. Критерий Коши для функций.
- •27. Непрерывность функции. Точки разрыва и их классификация. Односторонняя и кусочная непрерывность.
- •28.Локальные свойства непрерывных функций.
- •29.Глобальные свойства непрерывных функций. Теорема Больцано-Коши.
- •30.Глобальные свойства непрерывных функций. Теоремы Вейерштрасса.
- •31) Теорема о существовании и непрерывности обратной функции
- •32) Равномерная непрерывность. Теорема кантора
- •33) Непрерывность элементарных функций
- •34. Дифференцируемые функции. Определение производной функции в точке. Условия дифференцируемости функции в точке.
- •36. Односторонние и бесконечные производные.
- •43.Производные и дифференциалы высших порядков. Формула Лейбница. Неинва-
- •44. Локальная формула Тейлора. Единственность многочлена Тейлора.
- •45. Представление остаточного члена в формуле Тейлора в формах Лагранжа и Коши.
- •46. Разложение по ф-ле Маклорона важн элемент ф-ий
- •47. Многочлен Тейлора как многочлен наилучшего приближения функции в окрестности данной точки.
- •50 Выпуклость графиков функции.
- •51. Точки перегиба.
- •52 Асимптоты графика функции.
- •52(Продолжение)
36. Односторонние и бесконечные производные.
DF. Принято говорить что функция f имеет в т. x бесконечную производную если в этой т. она удовлетворяет двум условиям
Функция f непрерывна в т. x
lim (h→0)
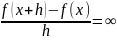
Односторонними производн ф-ии
f:X→R в т.x0єX
назыв след пределы:
производная слева
f’-(x0)=lim(f(x)-f(x0))/(x-x0) [x→ x0-0 и x< x0]= lim(f(x+h)-f(x))/h [h→-0, h<0]
производн справа
f’+(x0)=lim(f(x)-f(x0))/(x-x0) [x→ x0 +0и x> x0]= lim(f(x+h)-f(x))/h [h→+0].
37. Производная и арифметические операции.
38. Производная композиции. Производная обратной функции. Инвариантность формы первого дифференциала.
39.
Производные функций, заданных
параметрически и неявно.


40.Нахождение производных некоторых функций. Таблица производных.
41. Основные теоремы дифференциального исчисления (теоремы Ферма, Ролля, Лагранжа, Коши).
42. Правило Лопиталя раскрытия неопределенностей
1.
Неопределённость вида
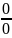 . Теор1: Пусть
функции f(x)
и g(x):
1)
Дифф-мы на (a
, b);
2)
. Теор1: Пусть
функции f(x)
и g(x):
1)
Дифф-мы на (a
, b);
2)
 ;
3)
g’(x)
≠0 во всех точках (a
, b);
4)
(конечный или ∞)
;
3)
g’(x)
≠0 во всех точках (a
, b);
4)
(конечный или ∞)
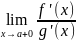 .
Тогда
.
Тогда

Док-во:
Доопределим
f
и g
в точке a:
f(a)=0,
g(a)=0.
Теперь f
и g
непрерывны справа и слева в точке а, и
удовлетворяет теореме коши о средних
значениях на любом отрезке (a
, x]
⊂
(a
, b).
∀x:
a<x<b ∃ξ=
ξ(x)∈(a
, x);
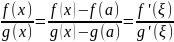 , причём
, причём
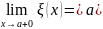
=>
если
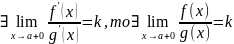 .
Замечание:
верно и для a-0
и просто a.
.
Замечание:
верно и для a-0
и просто a.
Теор2:
Пусть функции f(x)
и g(x):
1)
Диф-мы при x>c;
2)
 3)g’(x)
≠0 при x>c;
4)
(конечный или ∞)
3)g’(x)
≠0 при x>c;
4)
(конечный или ∞)
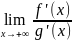 .
Тогда
.
Тогда
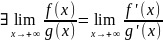
Док-во:
т.к. x->∞,
то без ограничения общности можно
считать с>0. Введём замену t= .
Тогда очевидно, что при (x->+∞)<=>(t->+0).
.
Тогда очевидно, что при (x->+∞)<=>(t->+0).
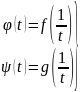 ∈
c(0
,
∈
c(0
,
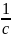 ).
∃
).
∃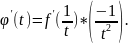 ∃
∃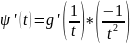 .
Тогда функция
.
Тогда функция
 и
и
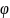 на интервале (0 ,
на интервале (0 ,
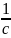 )
удовлетворяют условиям 1-ой теоремы.
Докажем:
)
удовлетворяют условиям 1-ой теоремы.
Докажем:
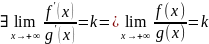 .
.
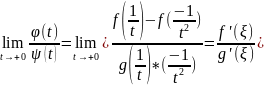 .
.
 .
Тогда, из теоремы 1 =>
.
Тогда, из теоремы 1 =>
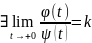 .
С другой стороны
.
С другой стороны
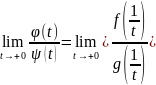 =
=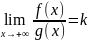 .
Замечание:
верно и для x->
-∞.
.
Замечание:
верно и для x->
-∞.
2.
Неопределённость вида
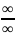 .
Теор3: Пусть
функции f(x)
и g(x):
1)
Дифф-мы на (a
, b);
2)
.
Теор3: Пусть
функции f(x)
и g(x):
1)
Дифф-мы на (a
, b);
2)
 ;
3)
g’(x)
≠0 во всех точках (a
, b);
4)
(конечный или ∞)
.
Тогда
;
3)
g’(x)
≠0 во всех точках (a
, b);
4)
(конечный или ∞)
.
Тогда
Док-во:Рассмотрим
случай
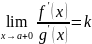 ∈R
и докажем его. Выберем
∈R
и докажем его. Выберем
 :
a<x<
:
a<x< <b.
На отрезке [x,
]
функ. f
и g
удовлетворяют условиям теоремы Коши
=> ∃
<b.
На отрезке [x,
]
функ. f
и g
удовлетворяют условиям теоремы Коши
=> ∃ ∈(x,
):
∈(x,
):
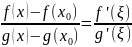 .
Вынесем
.
Вынесем
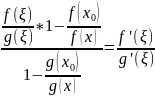 =>
=>
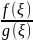 =
=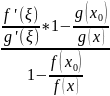 (1).
При заданом
,
как бы мы не выбирали т.
(1).
При заданом
,
как бы мы не выбирали т.
 ∈(a,
).
В силу 4-го условия:
∈(a,
).
В силу 4-го условия: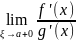 .
А в силу 2-го условия:
.
А в силу 2-го условия:
 .
В правой части равенства (1) нельзя просто
воспользоваться теор. (о пределе
произведений), т.к. эти пределы берутся
при разных условиях. 1)
.
В правой части равенства (1) нельзя просто
воспользоваться теор. (о пределе
произведений), т.к. эти пределы берутся
при разных условиях. 1)
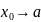 .
2)
.
2)
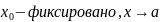 .
Тем не менее ∀
.
Тем не менее ∀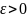 можно выбрать значение
,
чтобы величина
можно выбрать значение
,
чтобы величина
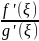 была сколь угодно близка к величине k
для
была сколь угодно близка к величине k
для
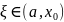 ,
а затем выбрать δ>0 чтобы дробь
,
а затем выбрать δ>0 чтобы дробь
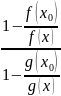 была близка к 1-це ∀x∈(a<
a+
δ). В результате при указывании x получаем
была близка к 1-це ∀x∈(a<
a+
δ). В результате при указывании x получаем
 .
k=
±∞. 3)
Неопределённости других видов.
.
k=
±∞. 3)
Неопределённости других видов.
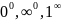 - можно раскрыть, если предварительно
прологорифмировать. Неопределённость
- можно раскрыть, если предварительно
прологорифмировать. Неопределённость
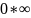 или
или
 - следует привести к виду
или
- следует привести к виду
или
43.Производные и дифференциалы высших порядков. Формула Лейбница. Неинва-
риантность формы высших дифференциалов.
Производные высших порядков
Если
функция
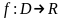 дифференцируема на некотором множестве
дифференцируема на некотором множестве
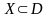 (т.е.
дифференцируема в каждой точке
(т.е.
дифференцируема в каждой точке
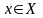 ),
),
то
можем рассмотреть новую функцию
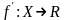
Производные
высших порядков определяются индуктивно
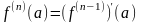 Определение
n-ой
производной можно записать в виде
предела
Определение
n-ой
производной можно записать в виде
предела
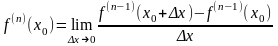 ,
n=1,2,3…
,
n=1,2,3…
!Подчеркнём,
что для существования n-й производной
в точке а, необходимо потребовать
существования всех предыдущих производных
,
 ,
,
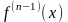 для x из некоторой окрестноти точки а
для x из некоторой окрестноти точки а
Формулы для производных элементарных функций

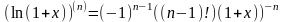
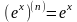

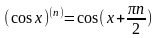 при
все
при
все
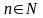
Функция называется n раз непрерывно дифференцмруема на некотором промежутке, если во всех точках этого множества она имеет непрерывные производные до порядка n включительно
Дифференциалы высших порядков.
Дифференциалом n-го порядка функции f в точке х называется однородная функция степени n от приращения h, определяемая след. равенством
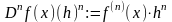
классический вид:
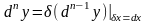
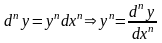 ,
n>1
,
n>1
Свойства дифференциалов высших порядков
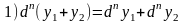
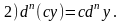 с-const
с-const
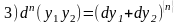
Формула Лейбница

Неинвариантность формы высших степеней
Дифференциалы высших порядков не обладают свойством инвариантности.
