7. Формула полной вероятности. Формула Бейеса.

Пусть событие А может появиться только при условии появления одного из несовместных событий В1, В2, …Bn, образующих полную группу. Поскольку заранее неизвестно, какое из событий В₁, В₂,…В_n появится, то эти события называют гипотезами. Пусть известны вероятности событий P(B₁), P(B₂),…,P(B_n), а также условная вероятность события А: P_B1(A), P_B2(A), … , P_Bn(A). Требуется найти вероятность появления события А. Тогда формула полной вероятности будет выглядеть так: P(A)=P(B₁)*P_B1(A)+P(B₂)*P_B2(A)+…+P(B_n)*P_Bn(A)= .

Пусть событие А может произойти только при наступлении одного из несовместных событий В₁, В₂,…В_n, образующих полную группу. Известны вероятности событий Bi и условные вероятности события А (PBI(A)). Тогда по формуле полной вероятности, вероятность события А есть: P(A)= . Найдем P_A(B_i). По теореме умножения (для независимых событий) имеем: P(AB₁)=P(A)*P_А(B₁)=P(B₁)*P_B1(A).Из двух частей выражаем P_A(B₁): P_A(B₁)=[P(B₁)*P_B1(A)] / P(A) .

Подставим P(A): P_А(B₁)= , Аналогичным образом рассуждая, можно получить вероятность любой гипотезы, произошедшей с появлением события А

P_А(B_i)= . Формула Бейеса. Формула используется для переоценки вероятностей гипотез, в том случае, если событие А уже произошло.

8. Повторение испытаний. Формула Бернулли.

опр: Если произведено несколько испытаний, причем вероятность наступления события А в каждом испытании не зависит от исходов другого испытания, то такие испытания называются независимыми относительно события А.

В разных испытаниях событие А может появляться как с различными вероятностями, так и с одной и той же вероятностью. В дальнейшем будем рассматривать только испытания, в которых событие А появляется с одной и той же вероятностью. Обозначим p – вероятность наступления события А в каждом испытании. q=1-p – вероятность не наступления события А в каждом испытании.

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), равна: , или , где q=1-p.

Вероятность того, что в n испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз;

а) P_n(0)+P_n(1)+…P_n(k-1); б) P_n(k+1)+P_n(k+2)+…+P_n(n); в) P_n(k)+P_n(k+1)+…+P_n(n); г)P_n(0)+P_n(1)+…+P_n(k).

9. Локальная и интегральная теоремы Лапласа.

Локальная теорема Лапласа: Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит ровно k раз(последовательность роли не играет), приближенно равна (тем точнее, чем больше n): . Здесь , .

- функция четная, т.е. . Значение функции находится по таблице.

Интегральная теорема Лапласа: Пусть событие А появляется в каждом испытании с одной и той же вероятностью p (0<p<1). Тогда вероятность того, что событие А появится в n испытаниях не менее k₁ и не более k₂ раз, определяется по формуле:

P_n(k₁,k₂)=Ф(х₂)-Ф(х₁), где Ф(х) – функция Лапласа: , , 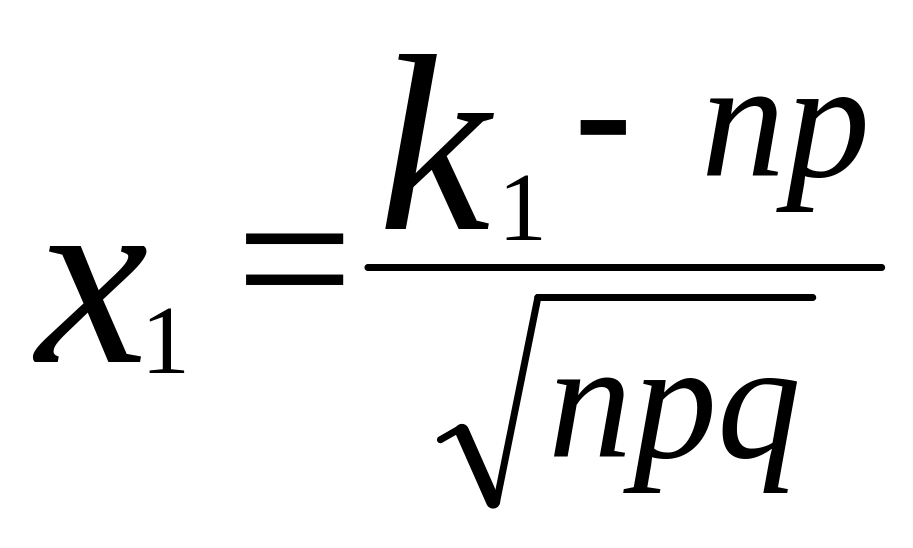. Функция Лапласа нечетная, т.е. , значение функции определяется по таблице, причем для x>5 - Ф(х)=0,5.